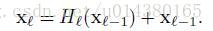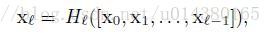resnet densenet
1.resnet的skip connection是通过eltwise相加的
2.resnet做detection的时候是在conv4_x的最后一层(也就是stage4的最后一层),因为这个地方stride为16
链接:https://www.zhihu.com/question/64494691/answer/271335912
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
炸问题已经很大程度上被normalized initialization and intermediate normalization layers解决了;
另一方面: 由于直接增加网络深度的(plain)网络在训练集上会有更高的错误率,所以更深的网络并没有过拟合,也就是说更深的网络效果不好,是因为网络没有被训练好,至于为啥没有被训练好,个人很赞同前面王峰的答案中的解释。
在ResNet中,building block:
H(x)是期望拟合的特征图,这里叫做desired underlying mapping
一个building block要拟合的就是这个潜在的特征图
当没有使用残差网络结构时,building block的映射F(x)需要做的就是拟合H(x)
当使用了残差网络时,就是加入了skip connection 结构,这时候由一个building block 的任务由: F(x) := H(x),变成了F(x) := H(x)-x
对比这两个待拟合的函数,文中说假设拟合残差图更容易优化,也就是说:F(x) := H(x)-x比F(x) := H(x)更容易优化,接下来举了一个例子,极端情况下:desired underlying mapping要拟合的是identity mapping,这时候残差网络的任务就是拟合F(x): 0,而原本的plain结构的话就是F(x) : x,而F(x): 0任务会更容易,原因是:resnet(残差网络)的F(x)究竟长什么样子?中theone的答案:
F是求和前网络映射,H是从输入到求和后的网络映射。比如把5映射到5.1,那么引入残差前是F'(5)=5.1,引入残差后是H(5)=5.1, H(5)=F(5)+5, F(5)=0.1。这里的F'和F都表示网络参数映射,引入残差后的映射对输出的变化更敏感。比如s输出从5.1变到5.2,映射F'的输出增加了1/51=2%,而对于残差结构输出从5.1到5.2,映射F是从0.1到0.2,增加了100%。明显后者输出变化对权重的调整作用更大,所以效果更好。残差的思想都是去掉相同的主体部分,从而突出微小的变化,看到残差网络我第一反应就是差分放大器
后续的实验也是证明了假设的, 残差网络比plain网络更好训练。因此,ResNet解决的是更好地训练网络的问题,王峰的答案算是对ResNet之所以好的一个理论论证吧.
第一个公式是ResNet的。这里的l表示层,xl表示l层的输出,Hl表示一个非线性变换。所以对于ResNet而言,l层的输出是l-1层的输出加上对l-1层输出的非线性变换。
第二个公式是DenseNet的。[x0,x1,…,xl-1]表示将0到l-1层的输出feature map做concatenation。concatenation是做通道的合并,就像Inception那样。而前面resnet是做值的相加,通道数是不变的。Hl包括BN,ReLU和3*3的卷积。
DenseNet的一个优点是网络更窄,参数更少,很大一部分原因得益于这种dense block的设计,后面有提到在dense block中每个卷积层的输出feature map的数量都很小(小于100),而不是像其他网络一样动不动就几百上千的宽度。同时这种连接方式使得特征和梯度的传递更加有效,网络也就更加容易训练。原文的一句话非常喜欢:Each layer has direct access to the gradients from the loss function and the original input signal, leading to an implicit deep supervision.直接解释了为什么这个网络的效果会很好。前面提到过梯度消失问题在网络深度越深的时候越容易出现,原因就是输入信息和梯度信息在很多层之间传递导致的,而现在这种dense connection相当于每一层都直接连接input和loss,因此就可以减轻梯度消失现象,这样更深网络不是问题
https://blog.csdn.net/u014380165/article/details/75142664/
问题:densenet什么时候效果比resnet好?
https://blog.csdn.net/gbyy42299/article/details/80434388