算法导论Part3: 二叉搜索树

1、概念

二叉搜索树性质：设x是二叉搜索树的一个节点，那么：

a) 对x左子树中任意节点y, y.key < x.key

b) 对x右子树种任意节点y, y.key >= x.key

 

2、数据结构

 1 struct TreeNode
 2 {
 3     TreeNode(int key): left(NULL), right(NULL), parent(NULL), key(key) {};
 4     TreeNode* left;
 5     TreeNode* right;
 6     TreeNode* parent;
 7     int key;
 8 };
 9 
10 class Tree
11 {
12 public:
13     Tree(): m_root(NULL) {};
14     TreeNode* minimum(TreeNode* );
15     TreeNode* maximum(TreeNode* );
16     void creat(int keys[], int n);
17     int insert(int key);
18     int remove(int key);
19     TreeNode* search(int key);
20     void walk(TreeNode *root);
21     TreeNode* get_root() const;
22 
23 protected:
24     inline TreeNode* node_creat(int key);
25     void transplant(TreeNode* x, TreeNode *y);
26 
27 private:
28     TreeNode* m_root;
29 };

 

3、算法

3.1 遍历

由二叉搜索树的性质，中序遍历的结果为keys的有序排列

1 void Tree::walk(TreeNode *root)
2 {
3     if (root == NULL)
4         return;
5     walk(root->left);
6     cout << root->key << " ";
7     walk(root->right);
8 }

3.2 最大/最小值

 1 TreeNode* Tree::minimum(TreeNode *root)
 2 {
 3     TreeNode *visit = root;
 4     if (visit == NULL)
 5         return NULL;
 6     while (visit->left != NULL)
 7         visit = visit->left;
 8     return visit;
 9 }
10 
11 TreeNode* Tree::maximum(TreeNode* root)
12 {
13     TreeNode *visit = root;
14     if (visit == NULL)
15         return NULL;
16     while (visit->right != NULL)
17         visit = visit->right;
18     return visit;
19 }

3.3 查找

 1 TreeNode* Tree::search(int key)
 2 {
 3     TreeNode* visit = m_root;
 4 
 5     while (visit != NULL)
 6     {
 7         if (key == visit->key)
 8             return visit;
 9         if (key < visit->key)
10             visit = visit->left;
11         else
12             visit = visit->right;
13     }
14 
15     return visit;
16 }

 

3.4 插入

插入时，必然是插入到某个叶子节点上，而不是两节点之间。

先查找到插入位置，然后插入。

 1 int Tree::insert(int key)
 2 {
 3     TreeNode* z = new TreeNode(key);
 4     TreeNode* x = m_root;
 5     TreeNode* y = NULL;
 6     while (x != NULL)
 7     {
 8         y = x;
 9         if (z->key < x->key)
10             x = x->left;
11         else
12             x = x->right;
13     }
14     z->parent = y;
15     if (y == NULL) // tree is empty
16         m_root = z;
17     else if (z->key < y->key)
18         y->left = z;
19     else
20         y->right = z;
21     
22     return 0;
23 }

 

3.5 删除

删除时，情况较复杂，对于待删除节点z：

IF z.left is NULL

　　replace z by z.right

ELSE IF z.right is NULL

　　replace z by z.left

ELSE // z 包含左右子树

　　找出z的后继y，即key大于z.key的最小节点, y在z的右子树中且y没有左子树

　　IF y.parent is z

　　　　replace z by y, 留下y.right

　　ELSE

　　　　replace z.right by y,

　　　　replace z by y

 

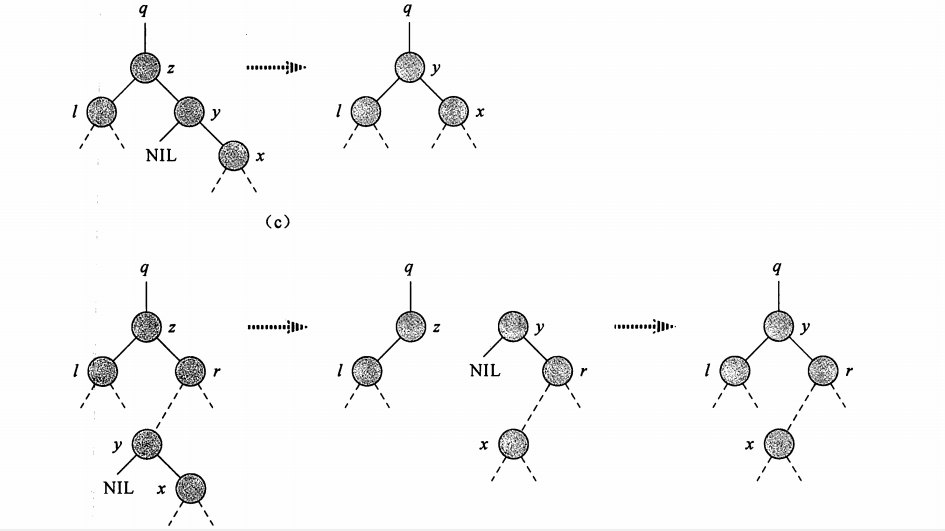
 1 // replace x by node y
 2 void Tree::transplant(TreeNode* x, TreeNode *y)
 3 {
 4     if (x->parent == NULL) // x is root
 5         m_root = y;
 6     else if (x->parent->left == x)
 7         x->parent->left = y;
 8     else
 9         x->parent->right = y;
10 
11     if (y != NULL)
12         y->parent = x->parent;
13 }
14 
15 int Tree::remove(int key)
16 {
17     TreeNode* y = NULL;
18     TreeNode* z = search(key);
19     if (z == NULL)
20         return -1;
21 
22     if (z->left == NULL)
23         transplant(z, z->right);
24     else if (z->right == NULL)
25         transplant(z, z->left);
26     else
27     {
28         y = minimum(z->right);
29         if (y->parent != z)
30         {
31             transplant(y, y->right); // replace y by right child
32             // let y be parent of z->right
33             y->right = z->right;
34             y->right->parent = y;
35         }
36         transplant(z, y);
37         y->left = z->left;
38         y->left->parent = y;
39     }
40 
41     return 0;
42 }

 

tips：源码

posted on 2015-05-31 11:44  ym65536  阅读(191)  评论(0)  编辑  收藏  举报