Java Heap
堆
堆是一种基于树的数据结构,是一种完全二叉树,堆中的所有的节点都按照特定的顺序排列。
在堆数据结构中,如果任意父节点的值都大于其子节点,则会产生一个大顶堆;反之,如果任意父节点的值都小于其子节点,则会产生一个小顶堆 。
上述这种父节点与子节点之间的关系被称为堆属性 。
二叉堆
由于二叉堆是一棵完全二叉树,它可以很容易的被表示为一个数组。在数组中,array[0] 代表根节点,且父节点与子节点的索引关系为:Left Child = 2 * Parent + 1 , Right Child = 2 * Parent + 2。
下图是一个大顶堆的树形结构表示:
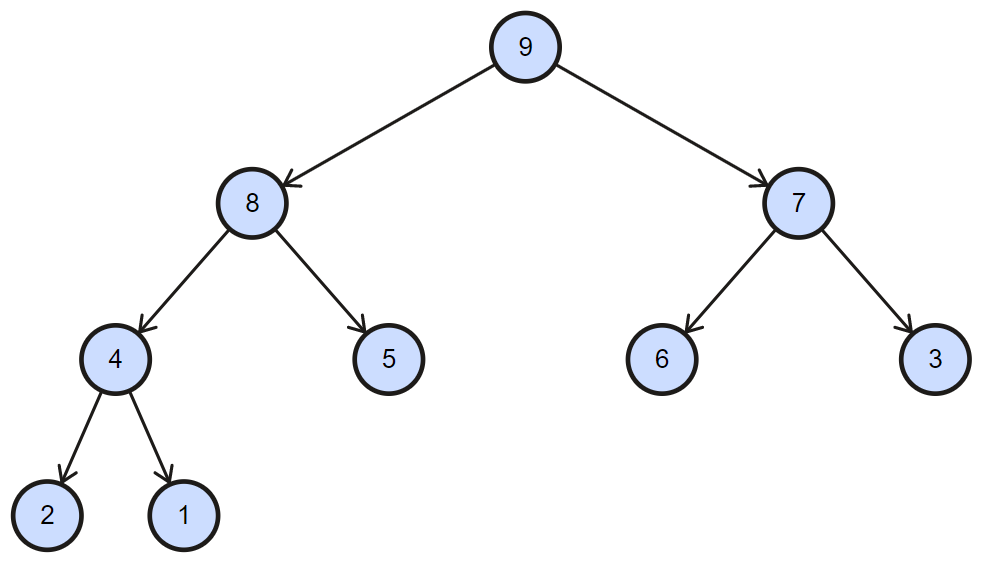
其数组表示如下:
[9, 8, 7, 4, 5, 6, 3, 2, 1]
小顶堆
插入元素
该过程包括两个步骤:
- 将元素插入到堆尾
- 执行 上浮 操作使其满足堆属性,该过程时间复杂度为 \(O(log N)\)
siftup操作逻辑: 对于小顶堆,若当前节点的元素小于其父节点,则交换这俩个节点的值,然后递归父节点,保证满足堆属性。
@SuppressWarnings("unchecked")
private void siftUp(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x;
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = minHeap[parent];
if (key.compareTo((E) e) >= 0) {
break;
}
minHeap[k] = e;
k = parent;
}
minHeap[k] = key;
}
删除元素
该过程包括3个步骤:
- 找到待删除元素的索引位置
- 将堆中最后一个元素移动到待删除元素的索引位置
- 对该索引位置元素执行 上浮 或 下沉 操作,该过程时间复杂度为 \(O(log N)\)
siftDown操作逻辑: 对于小顶堆,如果当前节点的值大于其左子节点或右子节点的值,则交换当前节点与子节点中的较小值,然后递归子树保证满足堆属性。
// 将最后一个元素移动到被删除位置
E moved = (E) minHeap[s];
minHeap[s] = null;
// 下沉
siftDown(i, moved);
if (minHeap[i] == moved) {
/**
* minHeap[i] == moved
* 表示没有下沉, 说明当前节点与子节点满足堆属性
* 执行上浮, 使得当前节点与父节点满足堆属性
*/
siftUp(i, moved);
if (minHeap[i] != moved) {
return moved;
}
}
private void siftDown(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x;
int half = heapSize >>> 1; // 非叶子节点
while (k < half) {
int child = (k << 1) + 1;
int right = (k << 1) + 2;
Object c = minHeap[child];
if (right < heapSize && ((Comparable<? super E>) c).compareTo((E) minHeap[right]) > 0) {
c = minHeap[child = right];
}
if (key.compareTo((E) c) <= 0) {
break;
}
minHeap[k] = c;
k = child;
}
minHeap[k] = key;
}
Java 实现
下述代码为小顶堆的实现,大顶堆的实现也是一样的,区别就是上浮 和 下沉 操作的交换逻辑与小顶堆相反。
package DataStructure;
import java.io.Serializable;
import java.util.NoSuchElementException;
public class MinHeap<E> implements Serializable{
private static final int DEFAULT_INITIAL_CAPACITY = 11;
transient Object[] minHeap;
private int heapSize = 0; // 当前堆中的元素个数
private int maxSize; // 堆中最大元素个数
public MinHeap() {
this(DEFAULT_INITIAL_CAPACITY);
}
public MinHeap(int initialCapacity) {
if (initialCapacity < 1) {
throw new IllegalArgumentException();
}
this.maxSize = initialCapacity;
this.minHeap = new Object[initialCapacity];
}
public MinHeap(Collection<? extends E> c) {
initElementsFromCollection(c);
heapify();
}
public int size() {
return heapSize;
}
public void clear() {
for (int i = 0; i < heapSize; i++) {
minHeap[i] = null;
}
heapSize = 0;
}
@SuppressWarnings("unchecked")
public E peek() {
return (heapSize == 0) ? null : (E) minHeap[0];
}
/**
* 插入元素到堆尾
* @param e
*/
public boolean add(E e) {
if (e == null) {
throw new NullPointerException();
}
int i = heapSize;
if (i >= maxSize) {
throw new NoSuchElementException("Heap is full!");
}
if (i == 0) {
minHeap[0] = e;
}
else {
siftUp(i, e);
}
return true;
}
/**
* 删除指定元素
* @param o
* @return
*/
public boolean remove(Object o) {
int i = indexOf(o);
if (i == - 1) {
return false;
}
else {
removeAt(i);
return true;
}
}
/**
* 弹出堆顶元素
* @return
*/
@SuppressWarnings("unchecked")
public E poll() {
if (heapSize == 0) {
return null;
}
int s = --heapSize;
E result = (E) minHeap[0];
E x = (E) minHeap[s];
minHeap[s] = null;
if (s != 0) {
siftDown(0, x);
}
return result;
}
private int indexOf(Object o) {
if (o != null) {
for (int i = 0; i < heapSize; i++) {
if (o.equals(minHeap[i])) {
return i;
}
}
}
return -1;
}
@SuppressWarnings("unchecked")
private E removeAt(int i) {
int s = --heapSize;
if (s == i) {
minHeap[i] = null; // 移除最后一个元素
}
else {
// 将最后一个元素移动到被删除位置
E moved = (E) minHeap[s];
minHeap[s] = null;
// 下沉
siftDown(i, moved);
if (minHeap[i] == moved) {
// 没有下沉, 说明当前节点与子节点满足堆属性
// 执行上浮, 使得当前节点与父节点满足堆属性
siftUp(i, moved);
if (minHeap[i] != moved) {
return moved;
}
}
}
return null;
}
@SuppressWarnings("unchecked")
private void siftUp(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x;
while (k > 0) {
int parent = (k - 1) >>> 1;
Object e = minHeap[parent];
if (key.compareTo((E) e) >= 0) {
break;
}
minHeap[k] = e;
k = parent;
}
minHeap[k] = key;
}
@SuppressWarnings("unchecked")
private void siftDown(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x;
int half = heapSize >>> 1; // 非叶子节点
while (k < half) {
int child = (k << 1) + 1;
int right = (k << 1) + 2;
Object c = minHeap[child];
if (right < heapSize && ((Comparable<? super E>) c).compareTo((E) minHeap[right]) > 0) {
c = minHeap[child = right];
}
if (key.compareTo((E) c) <= 0) {
break;
}
minHeap[k] = c;
k = child;
}
minHeap[k] = key;
}
private void initElementsFromCollection(Collection<? extends E> c) {
Object[] a = c.toArray();
if (a.getClass() != Object[].class) {
a = Arrays.copyOf(a, a.length, Object[].class);
}
int len = a.length;
for (int i = 0; i < len; i++) {
if (a[i] == null) {
throw new NullPointerException();
}
}
this.minHeap = a;
this.heapSize = a.length;
}
/**
* 根据 minHeap 数组建立小顶堆
*/
@SuppressWarnings("unchecked")
private void heapify() {
// 对所有非叶子节点执行下沉操作
for (int i = (heapSize >>> 1) - 1; i >= 0; i--) {
siftDown(i, (E) minHeap[i]);
}
}
}
优先级队列
PriorityQueue 是堆的一个实现,其默认为小顶堆,可以传入一个比较器使其实现为大顶堆。
public static void main(String[] args) {
// 默认创建小顶堆
PriorityQueue<Integer> minQueue = new PriorityQueue<>();
// 传入比较器, 创建大顶堆
PriorityQueue<Integer> maxQueue = new PriorityQueue<>((o1, o2) -> {return o2 - o1;});
for (int i = 0; i < 10; i++) {
minQueue.add(i);
maxQueue.add(i);
}
Iterator<Integer> it1 = minQueue.iterator();
Iterator<Integer> it2 = maxQueue.iterator();
while (it1.hasNext()) {
System.out.print(it1.next() + " ");
}
System.out.println();
while (it2.hasNext()) {
System.out.print(it2.next() + " ");
}
System.out.println();
}
输出结果为:
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
[9, 8, 5, 6, 7, 1, 4, 0, 3, 2]
堆排序
堆排序算法步骤如下 (升序排列):
- 对待排序数组建立小顶堆
- 依次弹出堆顶元素即堆中最小值
该算法时间复杂度为:\(O(NlogN)\)
public static void main(String[] args) {
int[] nums = {2, 3, 1, 6, 4, 7, 5, 8, 9};
List<Integer> list = Arrays.stream(nums).boxed().collect(Collectors.toList());
MinHeap<Integer> minHeap = new MinHeap<>(list);
int[] res = new int[nums.length];
int index = 0;
while(minHeap.size() != 0) {
res[index++] = minHeap.poll();
}
for (int i = 0; i < res.length; i++) {
System.out.print(res[i] + " ");
}
System.out.println();
}
输出结果为:[1, 2, 3, 4, 5, 6, 7, 8, 9]

