线段树学习

线段树(Segment Tree)

线段树是算法竞赛中常用的用来维护 区间信息 的数据结构，是一种二叉搜索树。

线段树可以在 \(O(log_2 N)\) 的时间复杂度实现 单点修改、区间修改、区间查询（区间求和，区间最大值，区间最小值）等操作。

Tips: 可以用线段树维护的问题必须满足区间加法，否则无法将大问题划分为子问题来解决。

区间加法

区间加法的问题需要满足对于 区间[L, R] 的问题答案可以由 区间[L, M] 和 区间[M+ 1, R] 的答案合并得到。

经典的区间加法问题

• 区间求和
• 区间最大值
• 区间最小值

线段树的基本结构

线段树将每个长度不为1的区间划分成左右两个区间递归求解，把整个线段划分为一个树形结构，通过合并左右两个子区间的信息来求得该区间的信息。这种数据结构可以方便的进行大部分的区间操作。

线段树（区间求和）样例：array = {1, 3, 5, 7, 9}, array.size = 5

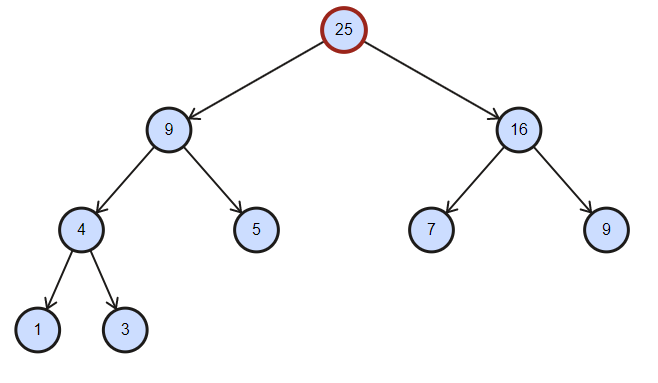
线段树主要是把一段大区间平均地划分成两段小区间进行维护（即区间 \([s, t]\) 会被划分为左区间 \([s, \frac{s + t}{2}]\) 和右区间 \([\frac{s + t}{2} + 1, t]\) ），再用小区间的值来更新大区间。既能保证正确性，又能使时间保持在O(logN)，因为这棵线段树是平衡的。

线段树存储方式

通常采用堆式存储法，即\(d_i\)的左子节点为\(d_{2*i + 1}\)，右子节点为\(d_{2*i + 2}\)。每一个线段树上的节点存储以下几个变量：区间左边界，区间右边界，区间的答案（如上图为区间的元素之和）。

以上图为例：

• 线段树的根节点代表整个数组所在的区间对应信息，即array[0:4]的元素之和
• 线段树的每一个叶节点对应数组每个单元素构成的区间array[i]对应的信息，\(0 \le i \le 4\)
• 线段树的每一个中间节点存储对应数组某一区间array[i:j]对应的信息，\(0 \le i < j \le 4\)

区间求和问题

线段树的构建

"""
array -> 输入数组
st -> 线段树数组
si -> 线段树数组当前节点索引
start & end -> 当前节点表示的线段起始和结束下标
"""
def constructSTUtil(array, st, si, start, end):
    if (start == end):
        st[si] = array[start]
        return st[si]
    
    mid = start + (end - start) // 2
    
    # 递归构建左子树和右子树
    st[si] = constructSTUtil(array, st, si * 2 + 1, start, mid) + \
             constructSTUtil(array, st, si * 2 + 2, mid + 1, end)
    
    return st[si]

def constructST(array, n):
    max_size = 4 * n
    st = [0] * max_size
    
    # 调用 constructSTUtil 构建线段树
    constructST(array, st, 0, 0, n - 1)
    
    return st

设根节点的深度为0，则线段树的深度\(\lceil log_{2} {n} \rceil\)，在堆式存储的情况下叶子节点的数量为\(2^{\lceil log_{2} n \rceil}\)(包括空的叶子节点)。且线段树是一棵完全二叉树，所以其节点总数量为\(2^{\lceil log_{2} n \rceil + 1} - 1\)，该函数在 \(n = 2^x + 1(x \in N_{+})\)时取得极大值，此时的节点数量为\(4n - 5\)。所以初始化线段树时，可以直接开辟一个4n大小的数组。

区间和查询

如果要查询区间 [left, right] 的和，则可以将其拆成最多为\(O(log_2 n)\)个极大的区间，然后合并这些区间即可得到 [left, right] 区间的和。

以上图为例，若查询区间为[3, 5]，无法直接获取该区间的和，但可以将其拆成[3, 3] 和 [4, 5] 两个区间，通过合并这两个区间的和得到整个区间的和。

"""
st -> 线段树数组
si -> 线段树数组当前节点索引
start & end -> 当前节点表示的起始和结束下标
left & right -> 查询区间的起始和结束下标
"""
def getSumUtil(st, si, start, end, left, right):
    if (left <= start and right >= end):
        return st[si]
    
    if (right < start or left > end):
        return 0;
    
    mid = start + (end - start) // 2
    
    return getSumUtil(st, 2 * si + 1, start, mid, left, right) +
           getSumUtil(st, 2 * si + 2, mid + 1, end, left, right)

def getSum(st, n, left, right):
    # 越界判断
    if (left < 0 or right > n - 1 or right < left):
        return -1
    
    return getSumUtil(st, 0, 0, n - 1, left, right)

单点修改

"""
st -> 线段树数组
si -> 线段树数组当前节点索引
start & end -> 当前节点表示的起始和结束下标
index -> 待修改节点在array中的下标
diff -> 修改前后节点的差值
"""
def updateValueUtil(st, si, start, end, index, diff):
   # 越界判断
   if (index < start or index > end):
       return;
   
   # 更新修改的节点和其子节点
   st[si] = st[si] + diff
   
   # 递归的修改左右子树
   if (start != end):
       mid = start + (end - start) // 2
       updateValueUtil(st, si * 2 + 1, start, mid, index, diff)
       updateValueUtil(st, si * 2 + 2, mid + 1, end, index, diff)
       
def updateValue(array, st, n, index, new_val):
   # 越界判断
   if (index < 0 or index > n - 1):
       return
   
   diff = new_val - array[index]
   array[index] = new_val
   
   updateValueUtil(st, 0, 0, n - 1, index, diff)

区间修改与懒惰标记

延迟对子节点信息的更改，从而减少不必要的操作次数。每次执行修改时，通过打标记的方式表明该节点对应的区间在某一次操作中被更改，但不更新该节点的子节点值。实质性的修改在下一次访问带有标记的节点时进行。

仍以上图为例，给区间 [3, 5] 的每个数加上一个常数1，可以找到两个区间 [3, 3] 和 [4, 5] 分别对应线段树数组的5号点和3号点，我们直接在这两个节点上进行修改，并打上标记。

"""
区间修改: 区间内加上某个值
"""
def update(left, right, delta, s, t, p):
    # [left, right] -> 修改区间, delta -> 变化量, [s, t] -> 当前区间, p -> 当前根节点, b -> 懒标记数组
    if left <= s and right >= t:
        # 当前区间为修改区间的子集, 直接修改当前区间根节点的值, 然后打标记, 结束修改
        d[p] = d[p] + (t - s + 1) * delta
        b[p] = b[p] + delta
        return
    
    mid = s + (t - s) // 2
    
    if b[p] and s != t:
        # 当前节点懒标记非空, 则更新两个子节点的值和懒标记
        d[p * 2 + 1] = d[p * 2 + 1] + b[p] * (mid - s + 1)
        d[p * 2 + 2] = d[p * 2 + 2] + b[p] * (t - mid)
        
        b[p * 2 + 1] = b[p * 2 + 1] + b[p]
        b[p * 2 + 2] = b[p * 2 + 2] + b[p]
        
        # 清空当前节点的标记
        b[p] = 0
    
    if left <= mid:
        update(left, right, delta, s, mid, p * 2 + 1)
    if right > mid:
        update(left, right, delta, mid + 1, t, p * 2 + 2)
    
    d[p] = d[p * 2 + 1] + d[p * 2 + 2]


"""
带懒标记的区间求和
"""
def getSum(left, right, s, t, p):
    if left <= s and right >= t:
        return d[p]
    
    mid = s + (t - s) // 2
    if b[p]:
        d[p * 2 + 1] = d[p * 2 + 1] + b[p] * (m - s + 1)
        d[p * 2 + 2] = d[p * 2 + 2] + b[p] * (t- s)
        
        b[p * 2 + 1] = b[p * 2 + 1] + b[p]
        b[p * 2 + 2] = b[p * 2 + 2] + b[p]
        
        b[p] = 0
    
    sum = 0
    if left <= m:
        sum += getSum(left, right, s, m, p * 2 + 1)
    if right > m:
        sum += getSum(left, right, m + 1, t, p * 2 + 2)
    return sum

区间最值问题

线段树的构建

以最大值问题为例！

"""
array -> 输入数组
st -> 线段树数组
si -> 线段树数组当前节点索引
start & end -> 当前节点表示的线段起始和结束下标
"""
def constructSTUtil(array, st, si, start, end):
    if start == end:
        st[si] = array[start]
        return st[si]
    
    mid = start + (end - start) // 2
    st[si] = max(constructSTUtil(array, st, si * 2 + 1, start, mid),
                constructSTUtil(array, st, si * 2 + 2， mid + 1, end))
    return st[si]

def constructST(array, n):
    max_size = 4 * n
    st = [0] * max_size
    
    constructSTUtil(array, st, 0, 0, n - 1)

区间最大值查询

"""
st -> 线段树数组
si -> 线段树数组当前节点索引
start & end -> 当前节点表示的起始和结束下标
left & right -> 查询区间的起始和结束下标
"""
def getMaxUtil(st, si, start, end, left, right):
    # 查询区间 完全包含于 当前节点表示区间
    if (left <= start and right >= end):
        return st[si]
    
    # 查询区间 与 当前节点表示区间 无交集
    if (end < left or start > right):
        return -1
    
    # 查询区间 与 当前节点表示区间 相交
    mid = start + (end - start) // 2
    return max(getMaxUtil(st, si * 2 + 1, start, mid, left, right),
              getMaxUtil(st, si * 2 + 2, mid + 1, end, left, right))

def getMax(st, n, left, right):
    if (left < 0 or right > n - 1 or right < left):
        print("Invalid Input.")
        return -1
    
    return getMaxUtil(st, 0, 0, n - 1, left, right)

单点修改

"""
st -> 线段树数组
si -> 线段树数组当前节点索引
start & end -> 当前节点表示的起始和结束下标
index -> 待修改节点在array中的下标
value -> index节点修改后的值
"""
def updateValue(array, st, si, start, end, index, value):
    if (index < start or index > end):
        print("Invalid Input")
        return
    
    if (start == end):
        array[index] = value
        st[si] = value
    else:
        # 递归修改子树
        mid = start + (end - start) // 2
        if (index >= start and index <= mid):
            updateValue(array, st, si * 2 + 1, start, mid, index, value)
        else:
            updateValue(array, st, si * 2 + 2, mid + 1, end, index, value)
        
        st[si] = max(st[2 * si + 1], st[2 * si + 2])
    
    return

代码测试

Build Segment Tree

"""
array -> 输入数组
st -> 线段树数组
si -> 线段树数组当前节点索引
start & end -> 当前节点表示的线段起始和结束下标
"""
def constructSTUtil(array, st, si, start, end):
    if (start == end):
        st[si] = array[start]
        return st[si]
    
    mid = start + (end - start) // 2
    
    # 递归构建左子树和右子树
    st[si] = constructSTUtil(array, st, si * 2 + 1, start, mid) + \
             constructSTUtil(array, st, si * 2 + 2, mid + 1, end)
    
    return st[si]

def constructST(array, n):
    max_size = 4 * n
    st = [0] * max_size
    
    # 调用 constructSTUtil 构建线段树
    constructSTUtil(array, st, 0, 0, n - 1)
    
    return st

Query for Sum of a given range

"""
st -> 线段树数组
si -> 线段树数组当前节点索引
start & end -> 当前节点表示的起始和结束下标
left & right -> 查询区间的起始和结束下标
"""
def getSumUtil(st, si, start, end, left, right):
    if (left <= start and right >= end):
        return st[si]
    
    if (right < start or left > end):
        return 0;
    
    mid = start + (end - start) // 2
    
    return getSumUtil(st, 2 * si + 1, start, mid, left, right) + \
           getSumUtil(st, 2 * si + 2, mid + 1, end, left, right)

def getSum(st, n, left, right):
    # 越界判断
    if (left < 0 or right > n - 1 or right < left):
        return -1
    
    return getSumUtil(st, 0, 0, n - 1, left, right)

Update a value

"""
st -> 线段树数组
si -> 线段树数组当前节点索引
start & end -> 当前节点表示的起始和结束下标
index -> 待修改节点在array中的下标
diff -> 修改前后节点的差值
"""
def updateValueUtil(st, si, start, end, index, diff):
    # 越界判断
    if (index < start or index > end):
        return;
    
    # 更新修改的节点和其子节点
    st[si] = st[si] + diff
    
    # 递归的修改左右子树
    if (start != end):
        mid = start + (end - start) // 2
        updateValueUtil(st, si * 2 + 1, start, mid, index, diff)
        updateValueUtil(st, si * 2 + 2, mid + 1, end, index, diff)
        
def updateValue(array, st, n, index, new_val):
    # 越界判断
    if (index < 0 or index > n - 1):
        return
    
    diff = new_val - array[index]
    array[index] = new_val
    
    updateValueUtil(st, 0, 0, n - 1, index, diff)

Tese Example

array = [1, 3, 5, 7, 9, 11]
n = len(array)

st = constructST(array, n)
print(f"Sum of values in given range = {getSum(st, n, 1, 3)}")
updateValue(array, st, n, 1, 10)
print(f"Sum of values in given range = {getSum(st, n, 1, 3)}")

Sum of values in given range = 15
Sum of values in given range = 22

实战练习

LeeCode 300：最长递增子序列

题目描述

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列，删除（不删除）数组中的元素而不改变其余元素的顺序。

• \(1 \le nums.length \le 2500\)
• \(-10^4 \le nums[i] \le 10^4\)

建立模型

方法一

• 这是一个经典的动态规划问题
• 确定dp数组及下标的含义，数组的含义为以 nums[i] 结尾的严格递增子序列的最大长度
• 初始化dp数组，dp[0] = 1
• 确定递推公式 dp[i] = Math.max(dp[i], dp[j] + 1) 0 <= j < i && nums[i] > nums[j]
• 确定遍历顺序 i -> 1~nums.length - 1, j -> 0~i - 1

代码实现

public int lengthOfLIS_DP(int[] nums) {
  if (nums.length == 0) {
    return 0;
  }

  int[] dp = new int[nums.length];
  dp[0] = 1;

  int res = 1;
  for (int i = 1; i < nums.length; i++) {
    dp[i] = 1;
    for (int j = 0; j < i; j++) {
      /* 查找 nums[i] 之前的最大长度 max(dp[j]) */
      if (nums[i] > nums[j]) {
        dp[i] = Math.max(dp[i], dp[j] + 1);
      }
    }

    res = Math.max(res, dp[i]);
  }

  return res;
}

方法二

• 使用动态规划的弊端就是查找 nums[i] 之前的最大长度开销大 O(N)，使得整个算法的时间复杂度上升到\(O(N^2)\)
• 我们可以使用线段树来提高查找的效率，将时间复杂度降低到 \(O(Nlog_2(N))\)

代码实现

public class SegmentTree {
  /**
   * LeeCode 300: 最长上升子序列
   * Segment Tree
   * array = [0, 0, ..., 0, 0]
   * array.length = max_value - min_value + 1
   * array[i] 表示以 min_value + i 结尾的最长递增子序列长度为 0
   * 
   * 线段树维护的最大值的意义是以 min_value + i 结尾的最长上升子序列的长度
   * 
   * 遍历 nums 的过程中, 逐步构建线段树, 最后返回线段树最大值即 tree[1]
   * @param nums
   * @return
   */
  int[] tree;
  public int lengthOfLIS(int[] nums) {
    if (nums.length == 0) {
      return 0;
    }

    int res;

    int max_value = Integer.MIN_VALUE;
    int min_value = Integer.MAX_VALUE;
    for (int num : nums) {
      max_value = Math.max(num, max_value);
      min_value = Math.min(num, min_value);
    }
    
    // array数组最大长度为 max_value - min_value + 1
    // 所以线段树数组直接初始化为4倍最大array长度
    tree = new int[4 * (max_value - min_value + 1)];

    for (int num : nums) {
      if (num == min_value) {
        // num = min_value, 说明前面没有比它小的数，最大长度只能是1
        update(1, 1, max_value - min_value + 1, 1, 1);
      }
      else {
        // 查找以 min_value ~ num - 1 结尾的上升子序列最大长度
        res = 1 + query(1, 1, max_value - min_value + 1, 1, num - min_value);
      
        // 更新 array[num - min_value + 1] 的值为 res
        update(1, 1, max_value - min_value + 1, num - min_value + 1, res);
      }
    }

    return tree[1];
  }


  public void update(int cur, int left, int right, int index, int val) {
    if (left == right) {
      tree[cur] = val;
      return;
    }

    int mid = left + (right - left) / 2;
    if (index <= mid) {
      update(cur * 2, left, mid, index, val);
    }
    else {
      update(cur * 2 + 1, mid + 1, right, index, val);
    }

    tree[cur] = Math.max(tree[cur * 2], tree[cur * 2 + 1]);
  }

  public int query(int cur, int left, int right, int L, int R) {
    if (L <= left && R >= right) {
      return tree[cur];
    }

    int res = 0;
    int mid = left + (right - left) / 2;
    if (L <= mid) {
      res = query(cur * 2, left, mid, L, R);
    }
    if (R > mid) {
      res = Math.max(res, query(cur * 2 + 1, mid + 1, right, L, R));
    }

    return res;
  }
}

参考文章

[1] Segment Tree | Set 1 (Sum of given range)

[2] Segment Tree | Set 2 (Range Maximum Query with Node Update)

[3] 数据结构 — 线段树