LeeCode 二叉树问题(三)
二叉树的应用问题
LeeCode 222: 完全二叉树的节点个数
题目描述
给你一棵 完全二叉树 的根节点
root,求出该树的节点个数。
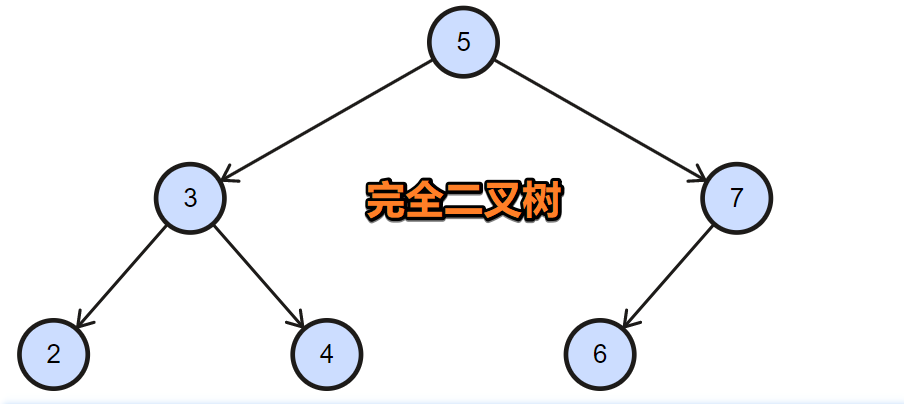
完全二叉树的定义
- 除最底层节点可能没填满外,其余每层节点树都达到最大值。
- 且最底层的节点都集中在该层最左边的若干位置。
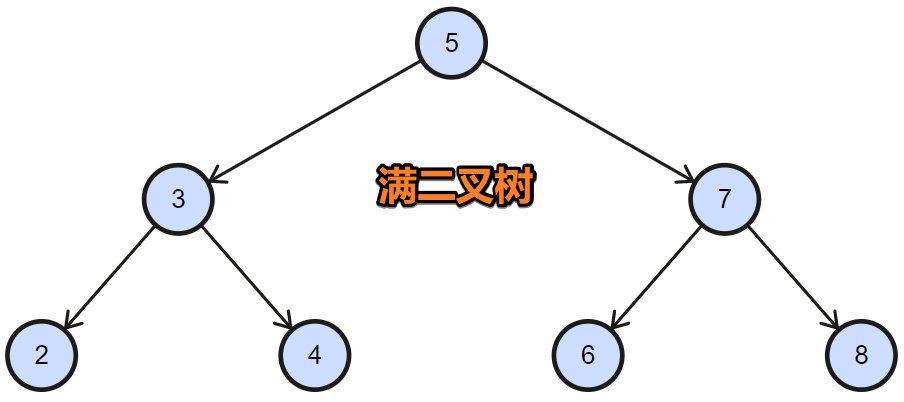
满二叉树的定义
- 每一层的节点数都达到最大值。
- 所以满二叉树是完全二叉树的一种。
建立模型
- 计算当前节点的左子树和右子树的高度
- 若相等,则说明以当前节点为根的数是一棵满二叉树,直接得到该数的节点数返回
- 若不相等,则递归计算当前节点的左子树和右子树
- 时间复杂度: \(O(log_2N)\) ,即从根节点到叶子节点的长度
代码实现
// Java 代码实现
public int countNodes(TreeNode root) {
if (root == null) {
return 0;
}
int left = 0, right = 0;
TreeNode node1 = root.left;
TreeNode node2 = root.right;
// 因为是完全二叉树,所有最底层肯定存在左边的节点
while (node1 != null) {
left += 1;
node1 = node1.left;
}
// 因为是完全二叉树,所有最底层可能不存在右边的节点
while (node2 != null) {
right += 1;
node2 = node2.right;
}
// 若左右子树高度相等,则返回
if (left == right) {
return (1 << (left + 1)) - 1;
}
// 若左右子树高度不想打,则递归计算
return countNodes(root.left) + countNodes(root.right) + 1;
}
LeeCode 110: 平衡二叉树
题目描述
给定一棵二叉树,判断它是否是高度平衡的二叉树。
一棵高度平衡二叉树的定义
二叉树每个节点的左右两个子树的高度差绝对值不超过1。
建立模型
自顶向下搜索
- 从根节点开始判断,左右子树的高度差
- 若符合,则递归判断左子节点和右子节点
- 若不符合,则返回
false - 直至遍历完所有节点
自底向上传播
- 从叶子节点开始判断,左右子树的高度差
- 若符合,则向父节点传播当前节点的高度
- 如不符合,则向父节点传播
false - 直至根节点
相较于自底向上的方法,自顶向下的过程中,存在大量的重复计算,时间复杂度较高。
代码实现
// 自顶向下, 最差情况可能需要对一个节点判断 logN 次
public boolean isBalanced(TreeNode root) {
if (root == null) {
return true;
}
boolean flag = Math.abs(getHeight(root.left) - getHeight(root.right)) <= 1;
return flag && isBalanced(root.left) && isBalanced(root.right);
}
// 计算以当前节点为根的树的高度
public int getHeight(TreeNode root) {
if (root == null) {
return 0;
}
return Math.max(getHeight(root.left), getHeight(root.right)) + 1;
}
// 自底向上实现
public boolean isBalanced(TreeNode root) {
return recursive(root) != -1;
}
public int recursive(TreeNode root) {
if (root == null) {
return 0;
}
int left = recursive(root.left);
if (left == -1) {
return -1;
}
int right = recursive(root.right);
if (right == -1) {
return -1;
}
if (Math.abs(left - right) <= 1) {
return Matn.max(left, right) + 1;
}
return -1;
}
LeeCode 113: 路径总和II
题目描述
给你二叉树的根节点
root和一个整数目标和targetSum,找出所有 从根节点到叶子节点 路径总和等于给定目标的路径。
建立模型
- 这是一个回溯类型的问题
- 采用深度优先搜索的方式遍历二叉树
- 若遍历到叶子节点且路径和等于目标和,则添加该路径
- 若遍历到叶子节点但路径和不等于目标和,则不符合要求
- 直至遍历完整棵树
代码实现
public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
List<Integer> temp = new ArrayList<>();
pathSumImpl(root, targetSum, temp, res);
return res;
}
public void pathSumImpl(TreeNode root, int target, List<Integer> temp, List<List<Integer>> res) {
if (root.left == null && root.right == null) {
if (root.val == target) {
temp.add(root.val);
res.add(new ArrayList<>(temp));
temp.remove(temp.size() - 1);
}
return;
}
// 向左子树搜索
if (root.left != null) {
temp.add(root.val);
pathSumImpl(root.left, target - root.val, temp, res);
temp.remove(temp.size() - 1);
}
// 向右子树搜索
if (root.right != null) {
temp.add(root.val);
pathSumImpl(root.right, target - root.val, temp, res);
temp.remove(temp.size() - 1);
}
return;
}
LeeCode 617: 合并二叉树
题目描述
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
建立模型
- 从根节点开始合并,然后递归地合并左右子节点
- 若树1当前节点和树2当前节点均不为空,则返回一个新的节点,节点值相加
- 若树1当前节点为空,树2当前节点不为空,则返回树2当前节点
- 若树1当前节点不为空,树2当前节点为空,则返回树1当前节点
- 若树1当前节点和树2当前节点均为空,则返回
null(该情况可以合并到3,4中)
代码实现
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if (root1 == null) {
return root2;
}
if (root2 == null) {
return root1;
}
TreeNode root = new TreeNode(root1.val + root2.val);
root.left = mergeTrees(root1.left, roo2.left);
root.right = mergeTrees(root1.right, roo2.right);
return root;
}
LeeCode 236: 二叉树的最近公共祖先
题目描述
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
p,q 均存在于给定的二叉树中。
建立模型
- 自底向上寻找p,q节点
- 若当前节点等于 p 或 q,则向父节点返回当前节点
- 若当前节点包含 p 或 q,则向父节点返回当前节点
代码实现
public TreeNode lowestCommonAncestor(TreeNode root) {
if (root == null || root == p || root == q) {
return root;
}
TreeNode left = lowestCommonAncestor(root.left);
TreeNode right = lowestCommonAncestor(root.right);
// left == null, 则p,q均位于当前root的右侧
if (left == null) {
return right;
}
// right == null, 则p,q均位于当前root的左侧
if (right == null) {
return left;
}
// left != null, right != null,则p,q位于当前root的两侧
return root;
}

