LeeCode 二叉树问题（一）

二叉树的遍历

二叉树节点定义

public class TreeNode {
  int val;
  TreeNode left;
  TreeNode right;
  
  TreeNode() {}
  TreeNode(int val) {
    this.val = val;
  }
  TreeNode(int val, TreeNode left, TreeNode right) {
    this.val = val;
    this.left = left;
    this.right = right;
  }
}

LeeCode 144: 二叉树的前序遍历

题目描述

给你一棵二叉树的根节点 root ，返回其节点值的前序遍历。

Java代码实现

递归实现

public List<Integer> preorderRecursive(TreeNode root) {
  List<Integer> res = new ArrayList<>();
  preorderRecursiveImpl(root, res);
  return res;
}

public void preorderRecursiveImpl(TreeNode root, List<Integer> res) {
  if (root == null) {
    return;
  }
  
  res.add(root.val);
  preorderRecursiveImpl(root.left, res);
  preorderRecursiveImpl(root.right, res);
  return;
}

迭代实现

递归实现本质上是维护了一个隐藏的栈结构，而在迭代时需要手动维护。

public List<Integer> preorderIterative(TreeNode root) {
  List<Integer> res = new ArrayList<>();
  if (root == null) {
    return res;
  }
  
  Stack<TreeNode> stack = new Stack<>();
  /**
   * 添加顺序: 根 -> 左 -> 右
   */
  while (root != null || !stack.isEmpty()) {
    while (root != null) {
      res.add(root.val);   
      stack.push(root);    
      root = root.left;    
    }
    
    root = stack.pop();
    root = root.right;
  }
  
  return res;
}

Morris 实现

public List<Integer> preorderMorris(TreeNode root) {
  List<Integer> res = new ArrayList<>();
  TreeNode cur = root;
  TreeNode prev = null;
  
  while (cur != null) {
    // 当前节点没有左子节点，则直接访问当前节点，并将指针指向右子节点
    if (cur.left == null) {
      res.add(cur.val);
      cur = cur.right;    // 通过 cur.right 返回父节点
      continue;
    }
    
    prev = cur.left;
    
    // 寻找当前节点左子节点的最右子结点
    while (prev.right != null && prev.right != cur) {
      prev = prev.right;
    }
    
    if (prev.right == null) {
      prev.right = cur;
      res.add(cur.val);    // 前序访问根节点
      cur = cur.left;
    }
    else {
      prev.right = null;
      cur = cur.right;
    }
  }
  
  return res;
}

LeeCode 94: 二叉树的中序遍历

题目描述

给你一棵二叉树的根节点 root，返回其节点值的中序遍历。

Java代码实现

递归实现

public List<Integer> inorderRecursive(TreeNode root) {
  List<Integer> res = new ArrayList<>();
  inorderRecursiveImpl(root, res);
  return res;
}

public void inorderRecursiveImpl(TreeNode root, List<Integer> res) {
  if (root == null) {
    return;
  }

  inorderRecursiveImpl(root.left, res);
  res.add(root.val);
  inorderRecursiveImpl(root.right, res);
  return;
}

迭代实现

public List<Integer> inorderIterative(TreeNode root) {
  List<Integer> res = new ArrayList<>();
  if (root == null) {
    return res;
  }
  
  Stack<TreeNode> stack = new Stack<>();
  /**
   * 添加顺序: 左 -> 根 -> 右
   */
  while (root != null || !stack.isEmpty()) {
    while (root != null) {
      stack.push(root);
      root = root.left;    
    }
    
    root = stack.pop();     
    res.add(root.val);
    root = root.right;
  }
  
  return res;
}

Morris 实现

Morris实现的核心想法是找到当前节点的左子节点的最右子结点，即当前节点中序遍历的前一个节点。

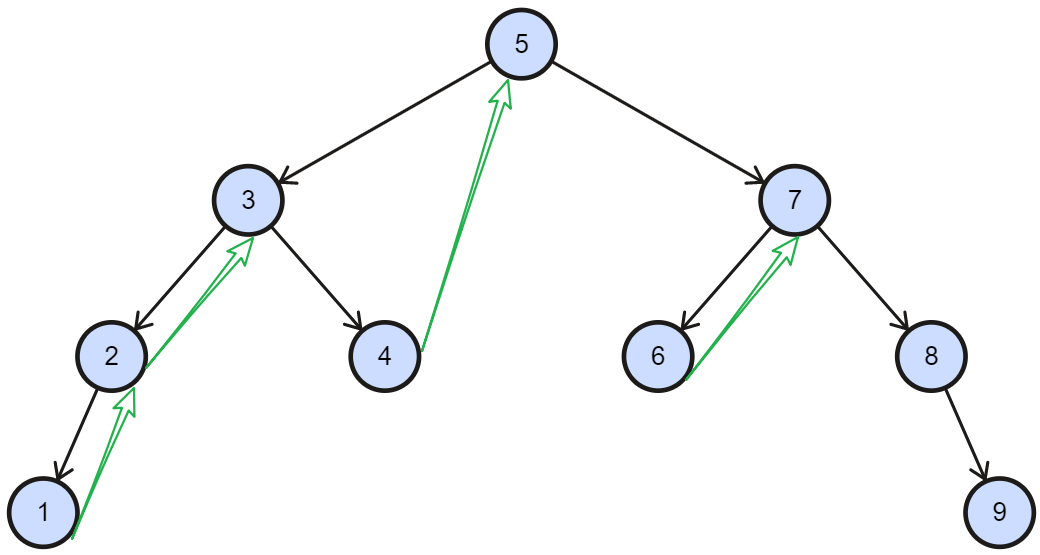
public List<Integer> inorderMorris(TreeNode root) {
  List<Integer> res = new ArrayList<>();
  TreeNode cur = root;
  TreeNode prev = null;
  
  while (cur != null) {
    // 当前节点没有左子节点，则直接访问该节点，然后将指针指向右子结点
    if (cur.left == null) {
      res.add(cur.val);
      cur = cur.right;    // 通过 cur.right 返回父节点
      continue;
    }
    
    prev = cur.left;
    
    // 寻找当前节点左子节点的最右子结点，即中序遍历中当前节点的前一个节点
    while (prev.right != null && prev.right != cur) {
      prev = prev.right;
    }
    
    if (prev.right == null) {
      prev.right = cur;
      cur = cur.left;
    }
    else {
      prev.right = null;
      res.add(cur.val);    // 中序访问根节点
      cur = cur.right;
    }
  }
  
  return res;
}

LeeCode 145: 二叉树的后序遍历

题目描述

给你一棵二叉树的根节点 root，返回其节点值的后序遍历。

Java代码实现

递归实现

public List<Integer> postorderRecursive(TreeNode root) {
  List<Integer> res = new ArrayList<>();
  postorderRecursiveImpl(root, res);
  return res;
}

public void postorderRecursiveImpl(TreeNode root, List<Integer> res) {
  if (root == null) {
    return;
  }

  postorderRecursiveImpl(root.left, res);
  postorderRecursiveImpl(root.right, res);
  res.add(root.val);
  return;
}

迭代实现

public List<Integer> postorderIterative(TreeNode root) {
  List<Integer> res = new ArrayList<>();
  if (root == null) {
    return res;
  }
  
  Stack<TreeNode> stack = new Stack<>();
  TreeNode previous = null;
  /**
   * 添加顺序: 左 -> 右 -> 根
   */
  while (root != null || !stack.isEmpty()) {
    while (root != null) {
      stack.push(root);
      root = root.left;
    }
    
    root = stack.pop();
    // 若右子树为空 或 右子树已经访问过，则添加根节点值
    if (root.right == null || root.right == previous) {
      res.add(root.val);
      previous = root;
      root = null;
    }
    else {
      stack.push(root);
      root = root.right;
    }
  }
  
  return res;
}

LeeCode 102: 二叉树的层序遍历

题目描述

给你一棵二叉树的根节点 root，返回其节点值的层序遍历。（即逐层地从左到右访问所有节点）。

建立模型

1. 这是一个广度优先搜索的问题，先遍历顶层所有节点，再往下遍历
2. 使用一个队列来维护遍历的节点
3. 使用变量size记录当前层节点个数

代码实现

public List<List<Integer>> levelOrder(TreeNode root) {
  List<List<Integer>> res = new ArrayList<>();
  if (root == null) {
    return res;
  }
  
  // 使用基于双向链表实现的队列维护
  Deque<TreeNode> deque = new LinkedList<>();
  deque.offer(root);    // 添加到队尾
  
  while (!deque.isEmpty()) {
    int size = deque.size();
    List<Integer> temp = new ArrayList<>();
    
    for (int i = 0; i < size; i++) {
      TreeNode node = deque.poll();    // 从队首取出
      temp.add(node.val);
      
      if (node.left != null) {
        deque.offer(node.left);
      }
      
      if (node.right != null) {
        deque.offer(node.right);
      }
    }
    
    res.add(new ArrayList<>(temp));
  }
  
  return res;
}