生存分析(Kaplan-Meier,Cox Regression)
一、背景
在某些场景下我们要判断一个事件能存活多久,这时候我们就需要使用生存分析相关的方法。例如,一些实验中小白鼠在某个时间段的生存概率;或者在日常的打车场景中,一个乘客呼叫了订单,这个订单在等待时间段中的存活概率。
二、风险函数、生存函数与删失数据
假设一个乘客发了一个打车订单,那么在不同时间点被乘客取消的概率密度函数则为风险函数(Hazard Function), 不取消的概率密度函数为生存函数(Survial Function)。 如这个订单在某个时间点被司机应答了,那么这个订单则退出了实验观察,那么我们称之为删失数据(Censored Data)。在生存分析中所有数据的时间口径划分都是当时相对的时间段。

因此由上述概念可以了解到,在生存分析当中我们主要的目的是得到比较准确的风险函数与生存函数。现有一些常用的方法供我们选择,Kaplan-Meier, Cox Regression等。
三、Kaplan-Meier
1、KM
对于单个变量的生存分析,我们可以采用 Kaplan-Meier,简称KM。KM的生存函数$S(t_{n})$与风险函数$h(t_{n})$分别为:
$$S(t_{n})=S(t_{n-1})*(1-\frac{d_{t_{n}}}{r_{{t_n}}})$$
$$h(t_{n})=\frac{d_{t_{n}}}{r_{{t_n}}}$$
- $d_{t_{n}}$为$t_{n-1}$到$t_{n}$时刻事件发生的数目,$r_{t_{n}}$为$t_{n-1}$时刻结束时事件存活数目
Example: 不同年龄段用户的订单生存时长与生存概率的关系(当前例子是年龄越大,对应的订单生存时长就越长)
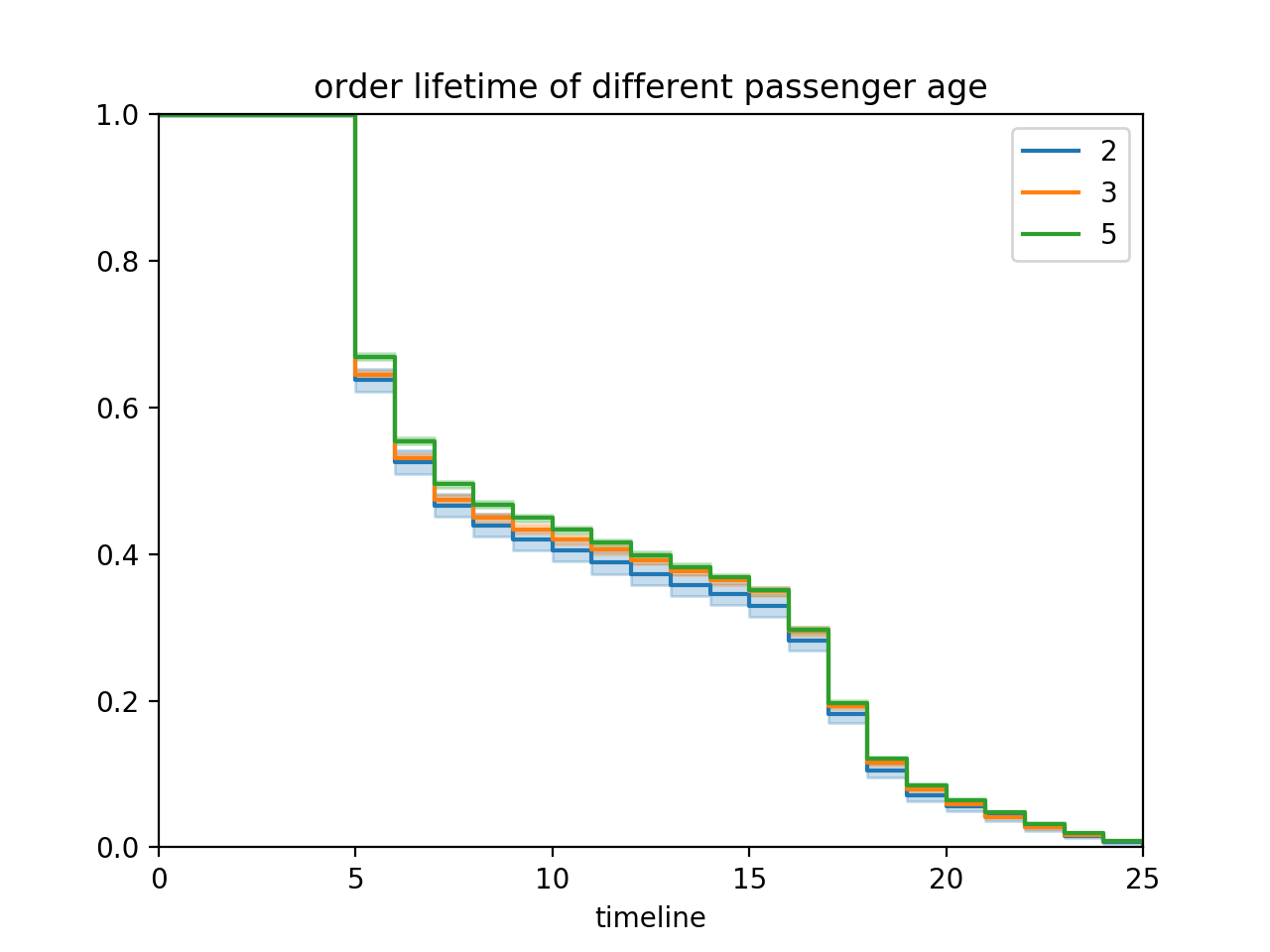
KM图虽有时候肉眼可以很直观看出不同变量和生存时长的关系,但是只能每次分析一个变量。KM曲线的假设检验方法有三种 log-rank, breslow, tarone, 这三种方法都为卡方检验,但是对于不同时间点的权重计算各为不同。
|
KM假设检验 (自由度为时间组数-1的卡方检验) |
各个时间点的权重 |
| log-rank | 个时间点权重均为1 |
| breslow | 各时间点存活个数 |
| tarone | 各时间点存活个数的平方根 |
2、卡方检验
卡方检验就是检验两个变量之间有没有关系,例如在这篇文章里面写的,打车用户的年龄与他们的等待时长有没有关系。卡方检验公式:
$$\chi ^{2}=\sum \frac{(observed-expected)^{2}}{expected}$$
然后再用求得的自由度,以及挑选的置信区间(一般为90%, 95%)来查表得到p值,然后通过卡方值与p值的比较得到我们是应该接受原假设还是拒绝原假设。
四、Cox Regression
1、Cox Regression的基本形式
Cox对风险函数的建模形式为:
$$h(t,X)=\lambda_{0}(t)exp(\beta X)$$
- $\lambda$是一个仅与时间相关的函数,其选择具有充分的灵活性,一种可能的选择是采用概率论中的Weibull分布,指数分布。
- $\beta$是模型的参数
2、参数的极大似然估计
极大似然估计的思想是让已经发生事件的概率最大。假设有3个年龄段用户A,B,C(分别为10岁,20岁,30岁)$X_{1}$, $X_{2}$,$X_{3}$, 然后在同一地点发出打车订单,但是由于周围没有车辆,他们分别在10秒、20秒、30秒又各自取消了订单。利用极大似然估计的思想,我们要在第10秒,第20秒,第30秒要分别令A,B,C取消订单的概率最大,则目标为
- $\max\ h(10, A)\ \min\ h(10,B)+h(10,C)$
- $\max\ h(20, B)\ \min\ h(20,C)$
- $\max\ h(30, C)$
将目标放在一个式子中。并且防止分母为0,分母加入分子项用来平滑,得
-
$\max\ \frac{h(10,A)}{h(10,A)+h(10,B)+h(10,C)}$
-
$\max\ \frac{h(20,B)}{h(20,B)+h(20,C)}$
- $\max\ \frac{h(30,C)}{h(30,C)}$
将三个式子合起来得到最终目标
$$\max\ \frac{h(10,A)}{h(10,A)+h(10,B)+h(10,C)}*\frac{h(20,B)}{h(20,B)+h(20,C)} *\frac{h(30,C)}{h(30,C)}$$
将其转化为似然函数为
$$L(\beta)=\frac{h(10,A)}{h(10,A)+h(10,B)+h(10,C)}*\frac{h(20,B)}{h(20,B)+h(20,C)} *\frac{h(30,C)}{h(30,C)}$$
消除基本风险函数$\lambda_{0}$ 得到最终通用的似然函数为:
$$L(\beta)=\prod_{i}^{N}\frac{exp(\beta\cdot X^{(i)})}{\sum_{j:t_{j}\geqslant t_{i}}exp(\beta\cdot X^{(j)})} $$
然后利用牛顿法(推导略,见参考部分)可以求解$\beta$参数,从而得到最终的模型。
五、生存模型的评估 concordance-index
concordance-index,简称C-index。定义:C-index = 一致的对子数/有用的对子数。 计算步骤
- 所有样本相互配对,共有 N*(N-1)/2 对,其中N为样本数
- 去除无法判断谁先到达事件终点的配对。例如配对中的A,B样本都没有到达事件终点。或者A比B的寿命短,但是A却没有到达事件终点就退出了实验。剩下的配对数目为M
- 计算剩下的配对中,预测结果和实际相一致的配对数记为K。(每个配对中,生存概率大的样本的确实生存时间越久,则记为与实际情况一致)
- 计算C-index = K/M

