图论的基本知识
一、柯尼斯堡七桥问题
图论的起源
在柯尼斯堡(今俄罗斯加里宁格勒)有一条河流,普列戈利亚河。河与陆地有七座桥相连。旅客进行游玩的时候,怎么才能走完所有的桥,并且一个桥只走一次?
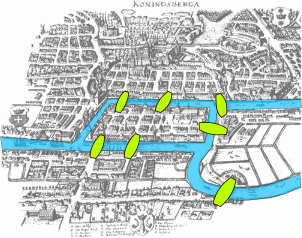
1735年,欧拉指出这是一个无解的问题。将桥视为线,将陆地视为点,欧拉将这个实际问题抽象成点与线的组合问题,因此问题变成从一点出发,在所有线直走一次的前提下,怎么能经过所有的线,然后回到该点?这个问题后来被欧拉归为一笔画问题,即从一点出发,用一个笔画就画出该完整的图。
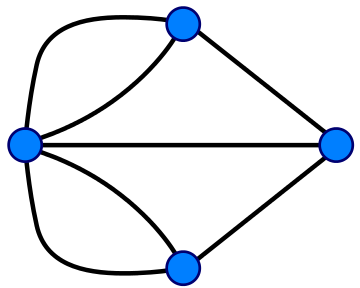
一些定义。
- 连有奇数条线的顶点称为奇顶点
- 连有偶数条线的顶点称为偶顶点
- 给定一个图,如果任意一个顶点,总有路径到达图中任意其他顶点,则这个图为连通图
- 能够通过一笔画遍历完成的图也叫做欧拉图,遍历的路径叫做欧拉路径,如果路径闭合则称为欧拉回路
若从某一点出发能再回到该点,这一点的边数必须是偶数(有出有回)。而柯尼斯堡七桥问题中的奇数顶点有4个,因此从任意一点出发,不存在走一步画能够走回该点的方法。因此柯尼斯堡七桥问题也无解。
一笔画定理
- 连通的无向图G有欧拉路径的充要条件是:G中奇顶点的数目等于0或2
- 连通的无向图G是欧拉环(两个相连的环为一个环)的充要条件是:G中每个顶点的度数为偶数
证明:
- 充分性:如果一个图为欧拉环,那么每个顶点的度都为2(有进有出),欧拉环也是欧拉图。如果一个欧拉图有奇顶点,那么奇顶点的个数为2(起点和终点),其他情况下无法每个边只走一次。因此如果一个图为欧拉图,奇顶点数为0(都为偶顶点,欧拉环)或2(一个起点,一个终点)。
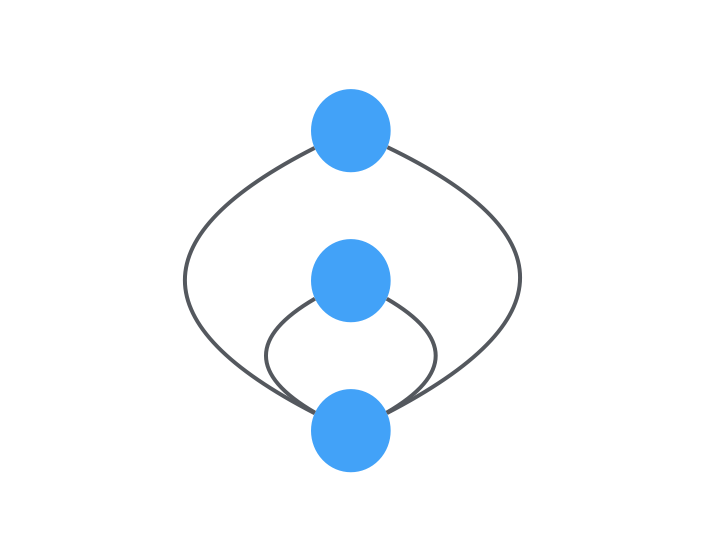
- 必要性:如果一个连通图都为偶顶点,则原图也就是由一个个环组成,因为相连的环也是一个环,则原图是欧拉环,欧拉环也是欧拉回路;如果一个连通图有两个奇顶点,将这两个奇顶点再用一条边两连则这个图为欧拉环,去掉这个边的话则这个连通图依然可以由一笔画完成。
一笔画定理也奠定了图论的发展的基础(参考wikipedia)
二、哈密顿图
由起点前往指定终点,图中经过其他所有顶点均一次的图。多有顶点的路径称为汉密尔顿路径,若G中通过且仅通过每个顶点一次,则这个圈称为汉密尔顿圈。

三、树
树是不包含回路的连通图。在树中次数为1的节点是叶,次数大于1的节点为分支节点。
表示:
- T<V,E>
- (n,m)树的含义为:树中有n个顶点,m条边
生成树:
设G=<V,E> 是一个连通图,T=<V',E'> 是G的一个子图,T是树,且V'=V,E'是E的子集,称T是G的生成树。
四、图的遍历
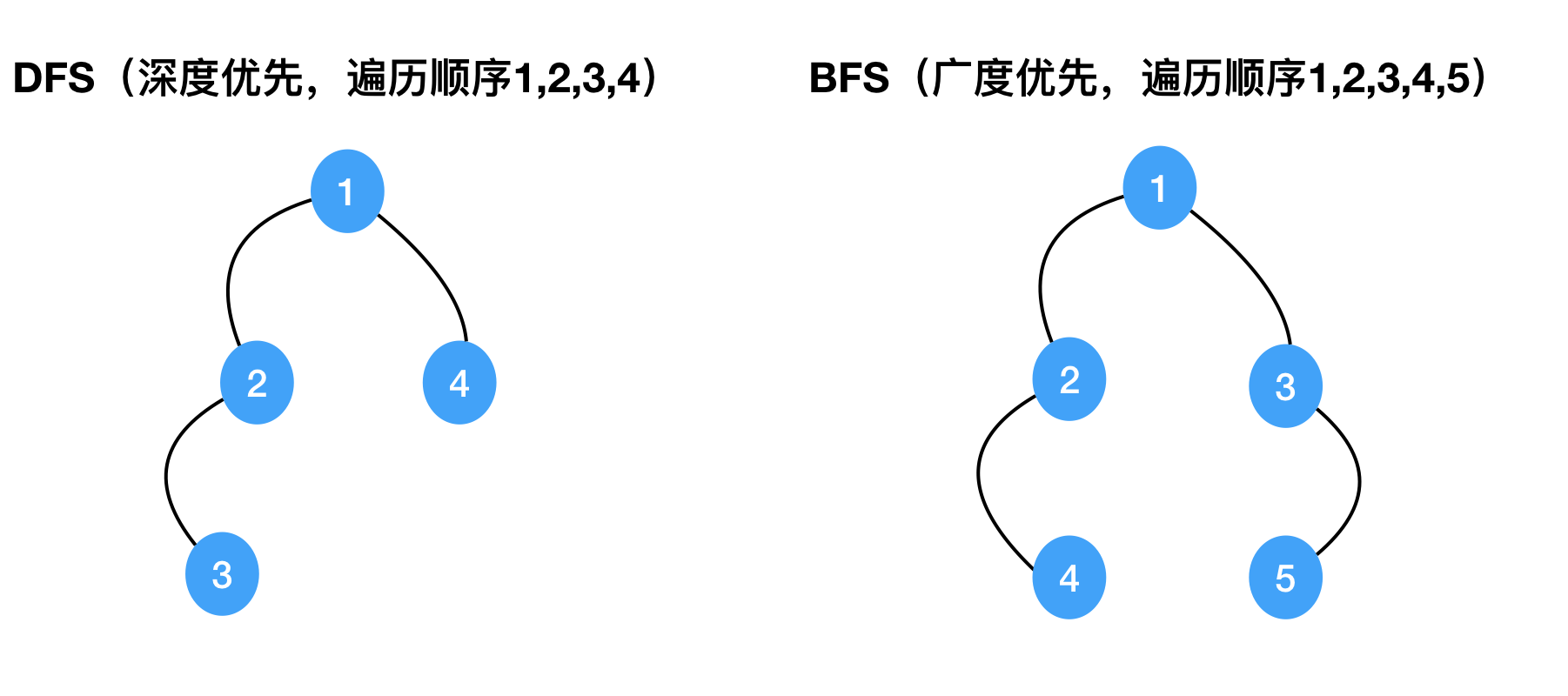
图的遍历分为深度优先遍历(沿着一条边遍历,从头到尾)和广度优先遍历(一层一层遍历)
五、图的表示方式
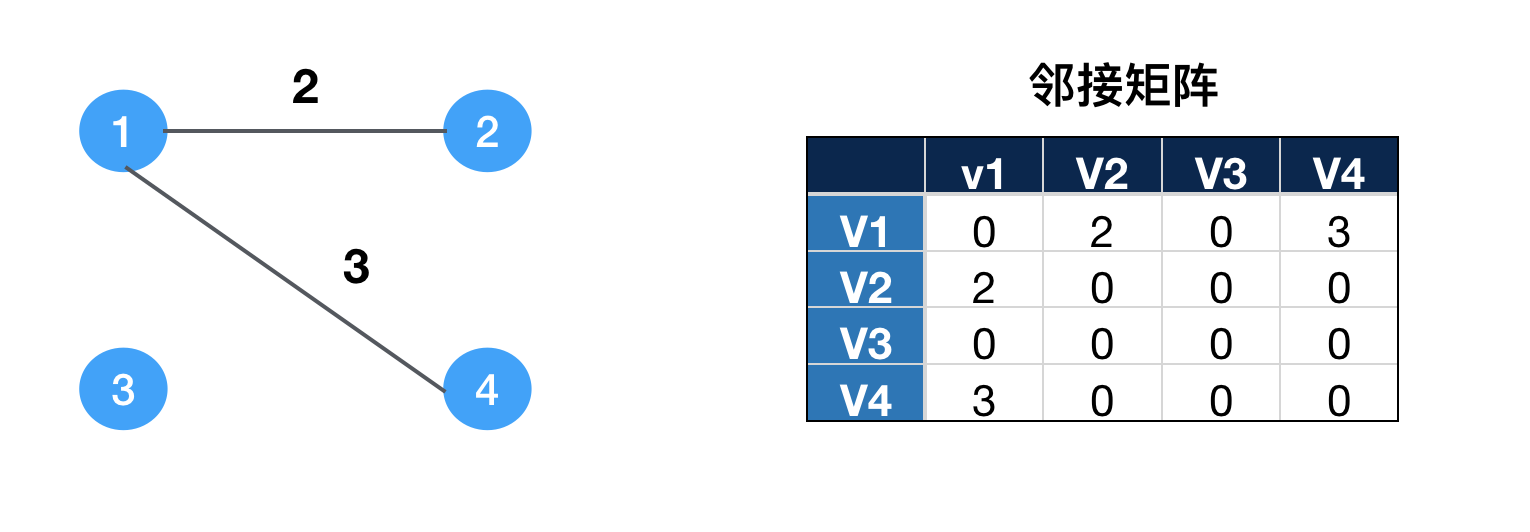
1、邻接矩阵
用二维数组表示矩阵。查找时间复杂度O(1),就是比较费内存
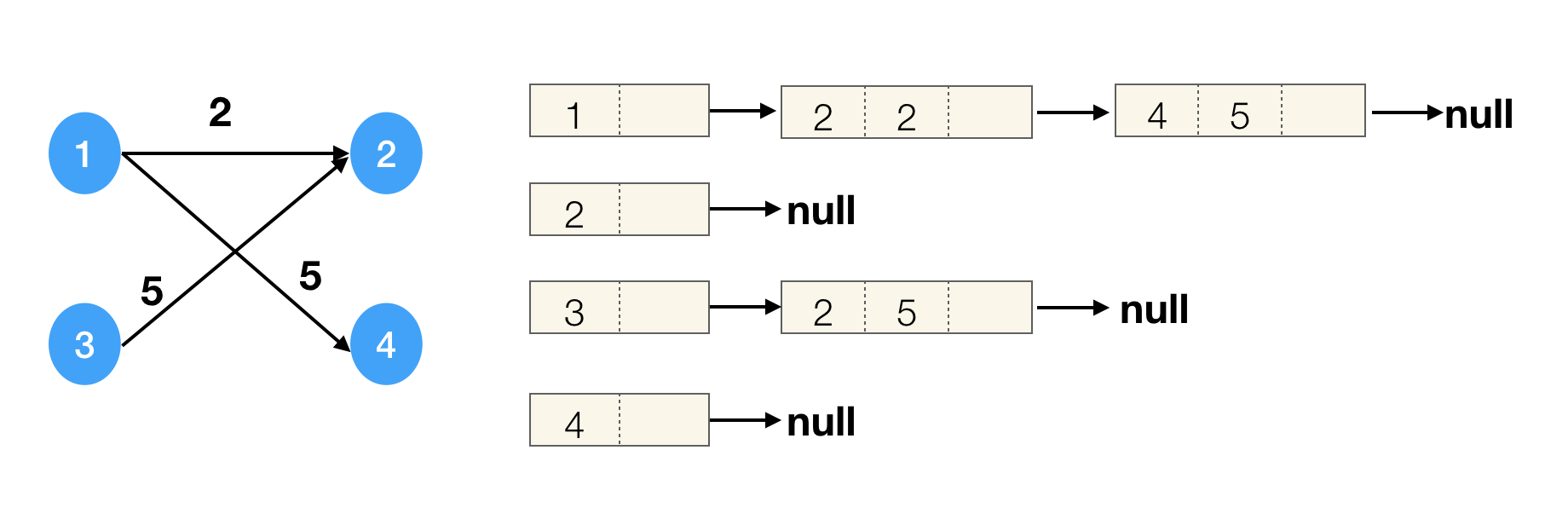
2、邻接表
当图比较稀疏的时候,用邻接表存储比较合适。
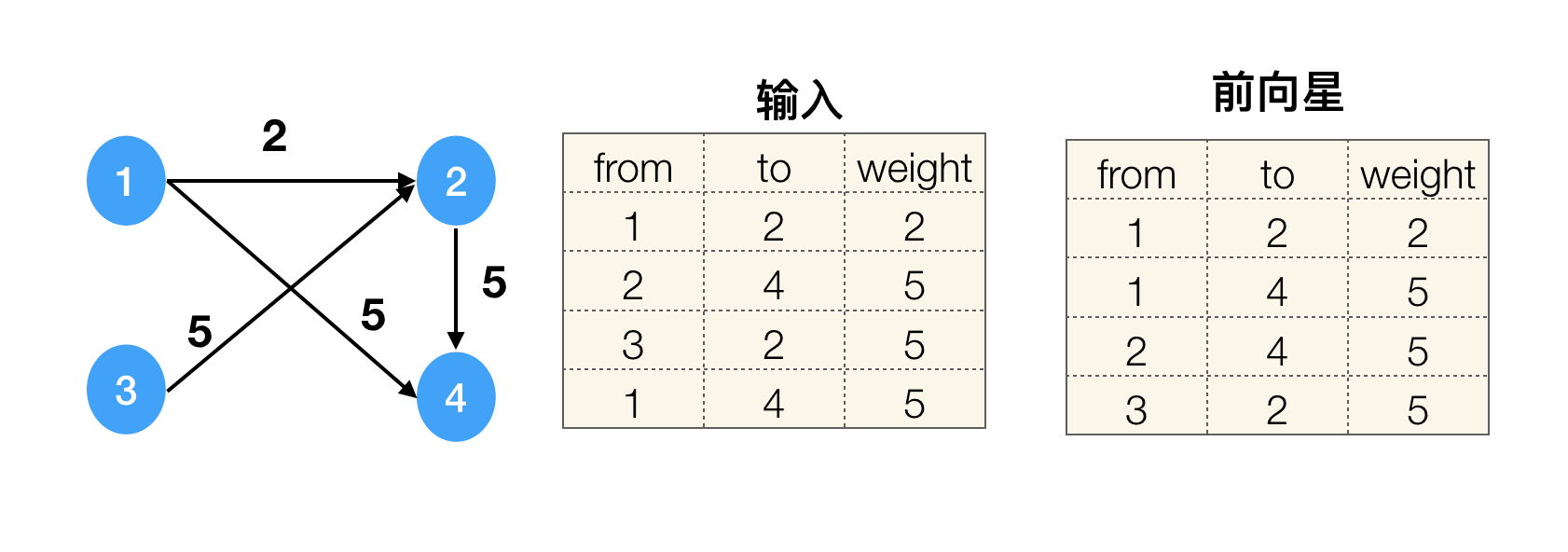
3、边集数组
常见的边集数组为前向星,以储存边的方式来存储图。构造方法如下:读入每条边的信息,将边存放在数组中,把数组中的边按照起点顺序排序(可以使用基数排序),前向星就构造完了。通常用在点的数目太多,或两点之间有多条弧的时候 (参考)。
前向星
链式前向星
前向星需要对边集数组进行排序。如果将边的数据结构设计成链表形式,则就不用对边集数组进行排序了
1 public class Edge { 2 private int from; 3 private int to; 4 private int weight; 5 private Edge next; 6 }
添加边
1 public void add(int f, int t, int w){ 2 edges[i].from = f; 3 edges[i].to = t; 4 edges[i].weight = w; 5 6 edges[i].next = head[f]; // head指向顶点f的第一条边的索引 7 8 head[f] = i++; 9 }
六、其他
一些概念
用 V= {v1, v2, ..., vn} 表示点集,E = {e1, e2, ..., en} 表示边集, 则图 可以表示称 G = <V, E>。
- 多重边,两个节点可以由多条边相连
- 图的阶,|V|为图的阶,即图中顶点的个数
- 完全图,任何两个顶点之间都有边相连为完全图

