方差与偏差,bias vs variance
一、方差与偏差文字与数学解释
(1)文字解释
- 偏差:预测值与真实值的差值
- 方差:预测值与训练数据集值的差值
(2)数学解释
- 对测试样本的预测值 $y-f(x;D)$
- 泛化误差:$Err(x)=E[(y-f(x;D))^{2}]$
- 测试样本的均值 $\bar{f}=E_{D}[f(x;D)]$,例如有5个样本分别为1,1,0,0,0 则$\bar{f}=0.4$
- 真实值$y_{D}$,数据集上的标签值,y是理论上正确的值。
对泛化误差进行分解:
$Err(x)$$=E[(y-f(x;D))^{2}]$
$=E_{D}[f(x;D)-\bar{f}+\bar{f}-y_{D}]$
$=E_{D}[(f(x;D)-\bar{f})^{2}] +E_{D}[(\bar{f}-y_{D})^{2}]+E_{D}[2(f(x;D)-\bar{f})(\bar{f}-y_{D})]$
$=E_{D}[(f(x;D)-\bar{f})^{2}]+E_{D}[(\bar{f}-y_{D})^{2}]$
$=E_{D}[(f(x;D)-\bar{f})^{2}]+E_{D}[(\bar{f}-y+y-y_{D})^{2}]$
$=E_{D}[(f(x;D)-\bar{f})^{2}]+E_{D}[(\bar{f}-y)^{2}]+E_{D}[(y-y_{D})^{2}]+2E_{D}[(\bar{f}-y)(y-y_{D})]$
$=E_{D}[(f(x;D)-\bar{f})^{2}]+(\bar{f}-y)^{2}+E_{D}[(y-y_{D})^{2}]$
- 方差 $E_{D}[(f(x;D)-\bar{f})^{2}]$
- 偏差 $(\bar{f}-y)^{2}$
- 误差 $E_{D}[(y-y_{D})^{2}]$
一些解释:
$E_{D}[2(f(x;D)-\bar{f})(\bar{f}-y_{D})]$ 这项展开为0
$2E_{D}[(\bar{f}-y)(y-y_{D})] 这项展开为0$
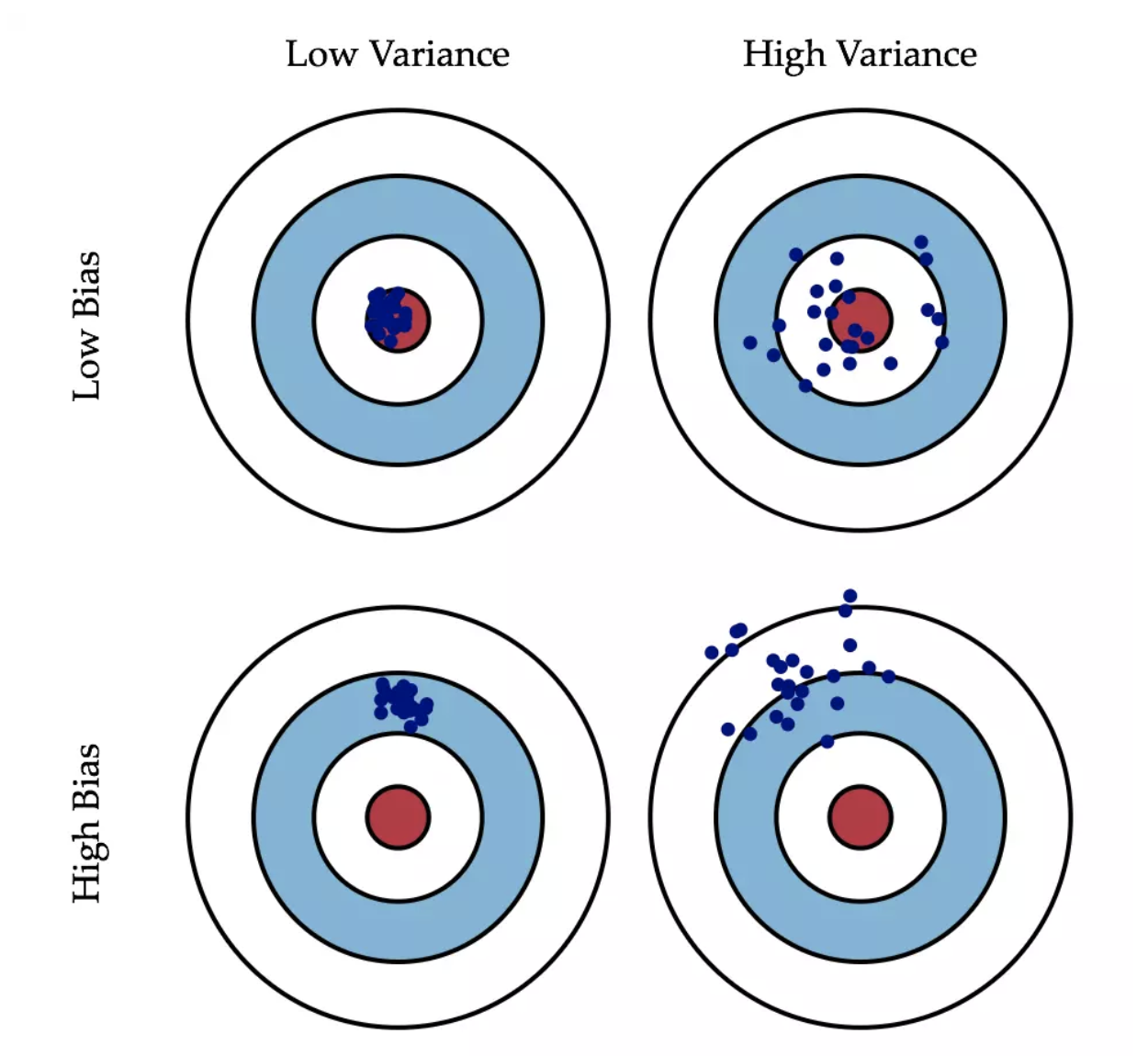
二、图形解释
- 中心红点为真实值
- 结合数学解释,如果预测值距离中心点近则为低偏差
- 结合数学解释,如果预测值比较密集则为低方差
三、测试集、训练集合的误差与方差、偏差之间的关系
| 测试集误差 | 训练集误差 | 方差 variace | 偏差 bias |
| 小 | 小 | 小 | 小 |
| 大 | 小 | 小(这种情况是过拟合) | 大 |
| 大 | 大 | 大 | 大 |
所以实际情况,我们的方差和偏差都越小越好。
谢谢!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号