AIC与BIC

首先看几个问题

1、实现参数的稀疏有什么好处？

一个好处是可以简化模型、避免过拟合。因为一个模型中真正重要的参数可能并不多，如果考虑所有的参数作用，会引发过拟合。并且参数少了模型的解释能力会变强。

 

2、参数值越小代表模型越简单吗？

是。越复杂的模型，越是会尝试对所有的样本进行拟合，甚至包括一些异常样本点，这就容易造成在较小的区间里预测值产生较大的波动，这种较大的波动也反应了在这个区间的导数很大，而只有较大的参数值才能产生较大的导数。因此复杂的模型，其参数值会比较大。

 

一、AIC

1、简介

AIC信息准则即Akaike information criterion，是衡量统计模型拟合优良性(Goodness of fit)的一种标准，由于它为日本统计学家赤池弘次创立和发展的，因此又称赤池信息量准则。它建立在熵的概念基础上，可以权衡所估计模型的复杂度和此模型拟合数据的优良性。

 

2、表达式

 

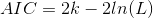
• k为参数数量
• L是似然函数

增加自由参数的数目提高了拟合的优良性，AIC鼓励数据拟合的优良性但是尽量避免出现过拟合的情况。所以优先考虑的模型应是AIC值最小的那一个，假设在n个模型中作出选择，可一次算出n个模型的AIC值，并找出最小AIC值对应的模型作为选择对象。

一般而言，当模型复杂度提高（k）增大时，似然函数L也会增大，从而使AIC变小，但是k过大时，似然函数增速减缓，导致AIC增大，模型过于复杂容易造成过拟合现象。

 

二、BIC

1、简介

 BIC= Bayesian Information Criterions，贝叶斯信息准则。

 

2、表达式

BIC=ln(n)k-2ln(L)

• L是似然函数
• n是样本大小
• K是参数数量

 

三、总结

1、共性

构造这些统计量所遵循的统计思想是一致的，就是在考虑拟合残差的同事，依自变量个数施加“惩罚”。

 

2、不同点

• BIC的惩罚项比AIC大，考虑了样本个数，样本数量多，可以防止模型精度过高造成的模型复杂度过高。
• AIC和BIC前半部分是一样的，BIC考虑了样本数量，样本数量过多时，可有效防止模型精度过高造成的模型复杂度过高。