RNN，LSTM
在DNN中，当前输出层的值只和当前输入值有关系。如果当前输出值不仅依赖当前输入值，也依赖于前面时刻的输入值，那么DNN就不适用了。因此也就有了RNN。
一、RNN
1、RNN结构
此RNN结构一共有T个时间序列，每个时间序列的输入为x，输出为y，流向下一个循环神经细胞的隐藏层状态为a。
2、RNN CELL单元以及前向传播
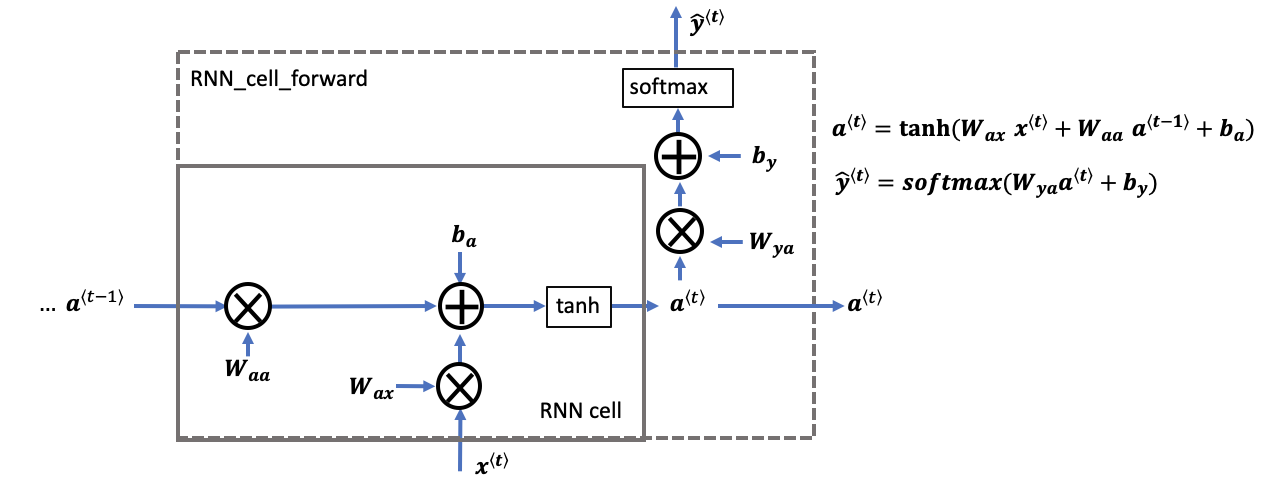
前向传播公式为上图右所示
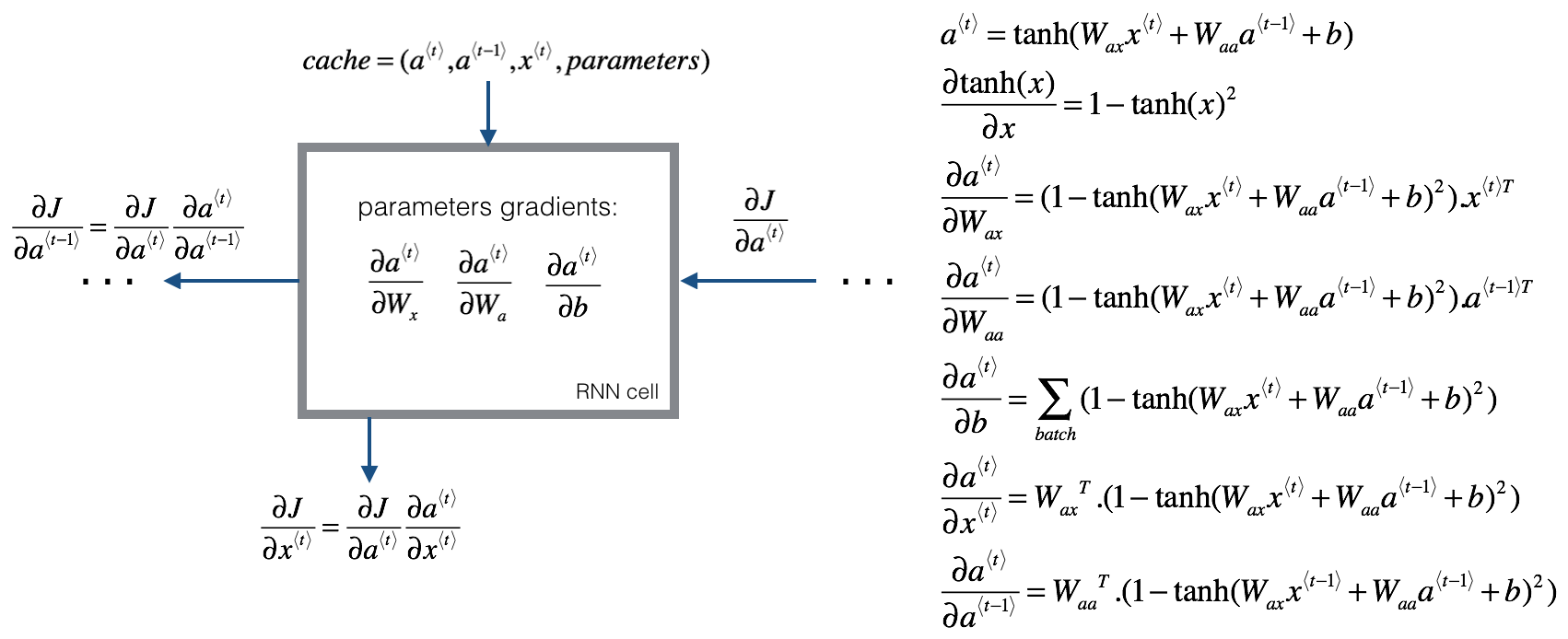
3、RNN反向传播
二、 LSTM
1、LSTM的结构
2、LSTM细胞单元
一共三个sigmoid激活函数，门控作用。两个tanh。
遗忘门（遗忘什么信息，因此使用sigmoid函数来控制，sigmoid的范围在0～1）：
$$\mathbf{\Gamma}_f^{\langle t \rangle} = \sigma(\mathbf{W}_f[\mathbf{a}^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_f) $$
更新门（什么信息用来更新细胞状态）：
$$\mathbf{\Gamma}_i^{\langle t \rangle} = \sigma(\mathbf{W}_i[a^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_i) $$
输出门（什么信息用来输出）：
$$ \mathbf{\Gamma}_o^{\langle t \rangle}= \sigma(\mathbf{W}_o[\mathbf{a}^{\langle t-1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_{o})$$
候选细胞状态
$$\mathbf{\tilde{c}}^{\langle t \rangle} = \tanh\left( \mathbf{W}_{c} [\mathbf{a}^{\langle t - 1 \rangle}, \mathbf{x}^{\langle t \rangle}] + \mathbf{b}_{c} \right) $$
最终细胞状态
$$ \mathbf{c}^{\langle t \rangle} = \mathbf{\Gamma}_f^{\langle t \rangle}* \mathbf{c}^{\langle t-1 \rangle} + \mathbf{\Gamma}_{i}^{\langle t \rangle} *\mathbf{\tilde{c}}^{\langle t \rangle} $$ （因此，根据遗忘门和更新门，不需要的信息当门控值为0或者很小时，求和的部分只取很小值，因为是求和操作，因此可以防止梯度消失）
隐藏细胞状态
$$ \mathbf{a}^{\langle t \rangle} = \mathbf{\Gamma}_o^{\langle t \rangle} * \tanh(\mathbf{c}^{\langle t \rangle})$$
输出
$$\mathbf{y}^{\langle t \rangle}_{pred} = \textrm{softmax}(\mathbf{W}_{y} \mathbf{a}^{\langle t \rangle} + \mathbf{b}_{y})$$
