深度学习中的激活函数
一、梯度消失与梯度爆炸
1、在DNN学习(二)反向传播中,观察公式三(3),为了求隐藏层参数的其中一步。根据链式法则,有

重新复习一下,J为损失函数。o为神经元的值,也是输入通过激励函数之后的值,z为上一层的神经元的线性变换的值。
2、那么下面上面式子中的这一步就是对激励函数的求导:

3、如果隐藏层数越来越多,那么公式将越来越长,对激励函数的求导会越来越多:
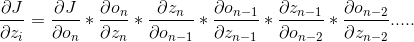
如果使用不恰当的激活函数则,由于乘积越来越多,则会造成梯度消失,或者梯度爆炸。
以sigmoid为例子:
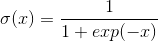
其导数
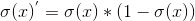
可以得到最大值为0.25。因此如果当其更小并且乘积项越来越多就会造成梯度消失,这样会影响优化效率,可能迭代了很多次,参数基本都没什么变化。
同理如果导数很大的话,乘积项很多则会造成梯度爆炸。参数一直在震荡,不利于调参数。
二、tanh
1、公式
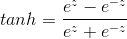
变换可得到:
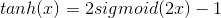
2、对其求导数,最大值为1,因此仍然会存在梯度消失的问题。
但是tanh是以0为中心的,这一点比sigmoid激活函数要好(这查了几篇文章,还是没有搞懂为什么)。
三、SOFTMAX
1、公式
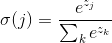
2、一般用于多分类问题。上述各个sigma(j)加起来为1。
四、RELU
1、公式:
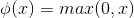
2、在x>0时候,其导数均为1,就不会存在优化的问题。
3、缺点:
当x<0时候,输入总是零,就会得到死神经元。因为反向传播时候,导数也是0,那么根据链式法则整个公式都是0,因此参数就不会得到更新。
五、LEAKY RELU
1、公式
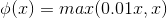
2、当x为负数时,导数依然有值,因此不会变为死神经元。
六、ELU
没有具体研究,只是看了下公式
1、公式:
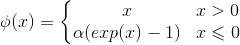
七、总结
sigmoid适合二分类的输出层,softmax适合多分类的输出层。
在隐藏层选取激活函数时,首先尝试RELU,然后可以用Leaky Relu 和Elu做对比。
谢谢!

