HashMap中的TreeNode，红黑树源码分析

在看HashMap的源码时候看到了TreeNode。因此需要对其进行一个了解。是一个红黑树。可以百度一下红黑树的数据结构。分析了下源码，还是比较枯燥的

红黑树的性质：本身是一个二叉查找树（所有左节点的值都比右节点的小）。另：

节点是红色或者黑色
根节点是黑色
每个叶节点（Nil节点，空节点）是黑色的
每个红节点对应的两个子节点都是黑色的（不可能有两个相连的红节点）。
从任意节点出发，到每个叶子节点都有相同的黑色节点。

这保证了红黑数是平衡的，从根到叶子的最长的可能路径不多于最短的可能路径的两倍长，因此插入、删除查找的最坏情况是有所保证的，与树的高度成正比。原因有两点：

最短的可能路径都是黑色节点。
最长的路径是红黑节点交替的路径。

因为从同一节点出发，到每一个叶子有相同的黑色节点，所以保证了最长路径是最短路径的两倍长。

一、成员变量与构造函数

 1  static final class TreeNode<K,V> extends LinkedHashMap.Entry<K,V> {
 2         //父节点
 3         HashMap.TreeNode<K,V> parent;  // red-black tree links
 4         //左节点
 5         HashMap.TreeNode<K,V> left;
 6         //右节点
 7         HashMap.TreeNode<K,V> right;
 8         //用来删除下一个节点用的，因此prev也就是上一个节点
 9         HashMap.TreeNode<K,V> prev;    // needed to unlink next upon deletion
10         //节点是否为红色
11         boolean red;
12         TreeNode(int hash, K key, V val, HashMap.Node<K,V> next) {
13             super(hash, key, val, next);
14         }
15 }

二、Function root

 1 /**
 2          * 返回包含此节点的树的根节点
 3          */
 4         final HashMap.TreeNode<K,V> root() {
 5             //定义两个TreeNode，一个是父节点指针，指向当前节点的parent，所以功能很明显了。就是遍历直到头节点
 6             for (HashMap.TreeNode<K,V> r = this, p;;) {
 7                 if ((p = r.parent) == null)
 8                     return r;
 9                 r = p;
10             }
11         }

三、Function checkInvariants

 1 /**
 2          * 不变性检查，保证红黑树的结构不改变。
 3          */
 4         static <K, V> boolean checkInvariants(HashMap.TreeNode<K, V> t) {
 5             HashMap.TreeNode<K, V> tp = t.parent, tl = t.left, tr = t.right,
 6                     tb = t.prev, tn = (HashMap.TreeNode<K, V>) t.next;
 7             if (tb != null && tb.next != t)
 8                 return false;
 9             if (tn != null && tn.prev != t)
10                 return false;
11             if (tp != null && t != tp.left && t != tp.right)
12                 return false;
13             if (tl != null && (tl.parent != t || tl.hash > t.hash))
14                 return false;
15             if (tr != null && (tr.parent != t || tr.hash < t.hash))
16                 return false;
17             if (t.red && tl != null && tl.red && tr != null && tr.red)
18                 return false;
19             if (tl != null && !checkInvariants(tl))
20                 return false;
21             if (tr != null && !checkInvariants(tr))
22                 return false;
23             return true;
24         }
25     }

四、Function moveRootToFront

 1 /**
 2          * 确保所给的root是第一个节点。也就是把所给的root移到第一个节点。确保桶的红黑树的跟节点是root
 3          */
 4         static <K, V> void moveRootToFront(HashMap.Node<K, V>[] tab, HashMap.TreeNode<K, V> root) {
 5             int n;
 6             if (root != null && tab != null && (n = tab.length) > 0) {
 7                 //根节点的位置
 8                 int index = (n - 1) & root.hash;
 9 
10                 //链表的操作，把root移到第一个节点。root的next指向原先的头节点，原先的头节点的prev指向root；
11                 //root的next的prev指向root的prev，root的prev指向root的next，即把root在prev和next中去掉
12                 HashMap.TreeNode<K, V> first = (HashMap.TreeNode<K, V>) tab[index];
13                 if (root != first) {
14                     HashMap.Node<K, V> rn;
15                     tab[index] = root;
16                     HashMap.TreeNode<K, V> rp = root.prev;
17                     if ((rn = root.next) != null)
18                         ((HashMap.TreeNode<K, V>) rn).prev = rp;
19                     if (rp != null)
20                         rp.next = rn;
21                     if (first != null)
22                         first.prev = root;
23                     root.next = first;
24                     root.prev = null;
25                 }
26                 //红黑树的一致性检查
27                 assert checkInvariants(root);
28             }
29         }

五、Function find

 1 /**
 2          * Finds the node starting at root p with the given hash and key.
 3          * The kc argument caches comparableClassFor(key) upon first use
 4          * comparing keys.
 5          */
 6         final HashMap.TreeNode<K, V> find(int h, Object k, Class<?> kc) {
 7             HashMap.TreeNode<K, V> p = this;
 8             do {
 9                 int ph, dir;
10                 K pk;
11                 HashMap.TreeNode<K, V> pl = p.left, pr = p.right, q;
12 
13                 //p的hash > 目标hash, 则查找左子树，否则右子树
14                 if ((ph = p.hash) > h)
15                     p = pl;
16                 else if (ph < h)
17                     p = pr;
18                 //找到则返回
19                 else if ((pk = p.key) == k || (k != null && k.equals(pk)))
20                     return p;
21                 //如果左节点是Null则找右子树，右节点是Null则找左子树
22                 else if (pl == null)
23                     p = pr;
24                 else if (pr == null)
25                     p = pl;
26                 //如果不按照hash比较，则按照比较器比较，查找左子树还是右子树
27                 else if ((kc != null ||
28                         (kc = comparableClassFor(k)) != null) &&
29                         (dir = compareComparables(kc, k, pk)) != 0)
30                     p = (dir < 0) ? pl : pr;
31                 //如果在右子树找到则直接返回
32                 else if ((q = pr.find(h, k, kc)) != null)
33                     return q;
34                 //否则在左子树查找
35                 else
36                     p = pl;
37             } while (p != null);
38             //否则返回Null
39             return null;
40         }

六、Function tieBreakOrder

 1 /**
 2          * 在像红黑树插入即节点的时候，为了确定相同hashCode的节点插入的顺序，
 3          * 设定了插入顺序的规则，结果一定是不想等的。非左即右。
 4          */
 5         static int tieBreakOrder(Object a, Object b) {
 6             int d;
 7 
 8             //会对两个类名相等的类进行比较
 9             if (a == null || b == null ||
10                     (d = a.getClass().getName().
11                             compareTo(b.getClass().getName())) == 0)
12                 //返回两个类内存地址的hashCode比较结果，小的或者相都是-1，否则1，并非是类的hashCode的比较
13                 d = (System.identityHashCode(a) <= System.identityHashCode(b) ?
14                         -1 : 1);
15             return d;
16         }

七、Function rotateLeft, 左旋

图片来源（https://blog.csdn.net/sun_tttt/article/details/65445754）

 1 static <K, V> HashMap.TreeNode<K, V> rotateLeft(HashMap.TreeNode<K, V> root,
 2                                                         HashMap.TreeNode<K, V> p) {
 3             //三个节点，右节点，parent的parent节点，右的左节点
 4             HashMap.TreeNode<K, V> r, pp, rl;
 5             //该节点不为null并且右节点不为null
 6             if (p != null && (r = p.right) != null) {
 7                 //因为是左旋，所以如果右节点的左节点如果不为null，则rl的根节点设为p
 8                 if ((rl = p.right = r.left) != null)
 9                     rl.parent = p;
10                 //如果左旋后的头节点为根节点，则根据红黑树的性质，颜色为黑色
11                 if ((pp = r.parent = p.parent) == null)
12                     (root = r).red = false;
13                 //因为是左旋，所以p的位置由pr取代，所以p的parent节点的p位置设为现在pr的位置。
14                 else if (pp.left == p)
15                     pp.left = r;
16                 else
17                     pp.right = r;
18                 //然后r的left是p，p的父节点是r
19                 r.left = p;
20                 p.parent = r;
21             }
22             return root;
23         }

八、Function rightRotate, 右旋

图片来源（https://blog.csdn.net/sun_tttt/article/details/65445754）

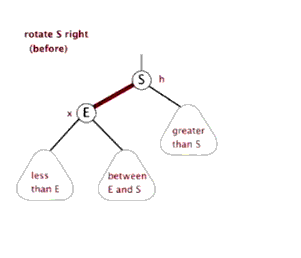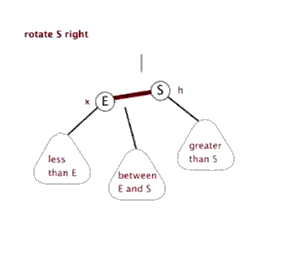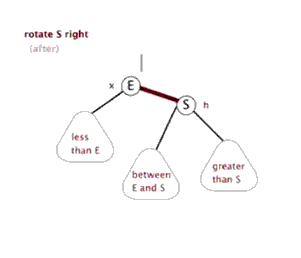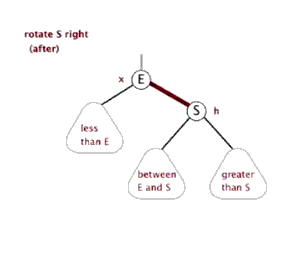
 1 static <K, V> HashMap.TreeNode<K, V> rotateRight(HashMap.TreeNode<K, V> root,
 2                                                          HashMap.TreeNode<K, V> p) {
 3             //定义3个节点，左节点，头节点的头节点，左节点的右节点
 4             HashMap.TreeNode<K, V> l, pp, lr;
 5             //要旋转的节点和左节点不为空时
 6             if (p != null && (l = p.left) != null) {
 7                 //根据右旋，（原）头节点的左节点为原先左节点的右节点，并且把其父节点设为原头节点，即p
 8                 if ((lr = p.left = l.right) != null)
 9                     lr.parent = p;
10                 //同样，如果现在的头节点为根节点的话，标记节点的颜色为黑色
11                 if ((pp = l.parent = p.parent) == null)
12                     (root = l).red = false;
13                     //头节点的头节点设定其自节点
14                 else if (pp.right == p)
15                     pp.right = l;
16                 else
17                     pp.left = l;
18                 //同样，根据右旋，指定现在的头节点的右节点为原先的头节点，原先的头节点的父节点为现在的头节点
19                 l.right = p;
20                 p.parent = l;
21             }
22             return root;
23         }

九、Function balanceInsertion 代码和图结合看很好理解过程，至于为什么会平衡还要分析。

图片来源https://blog.csdn.net/weixin_42340670/article/details/80550932

1.无旋转

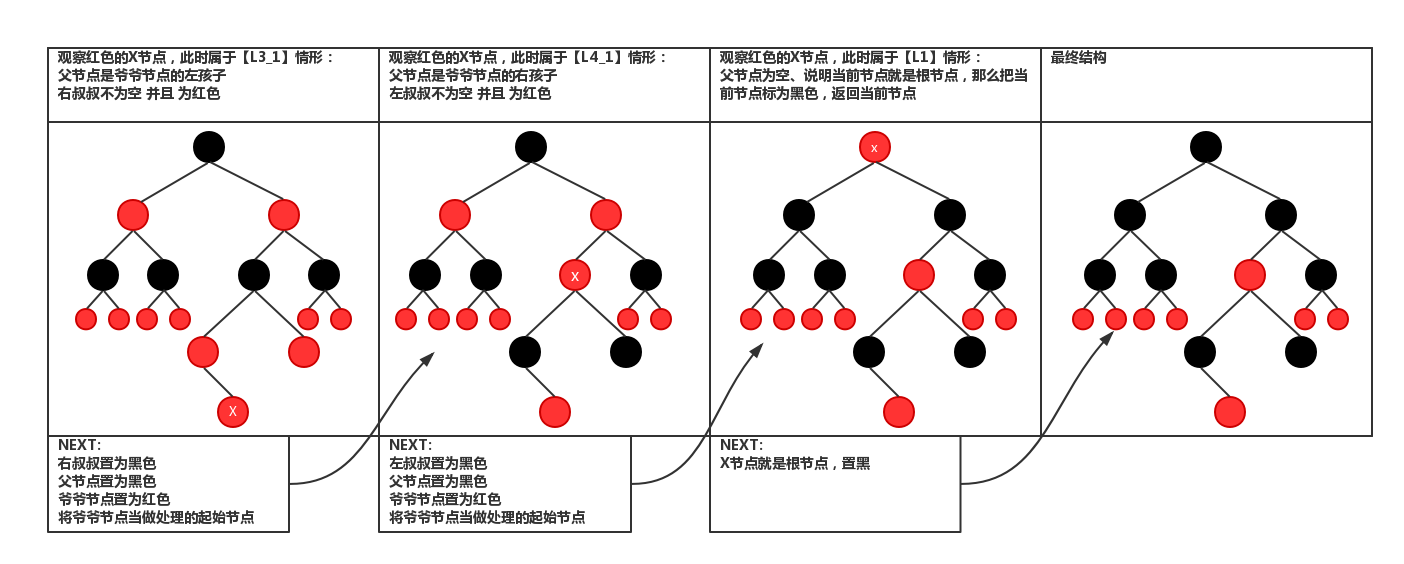
2.旋转情况1

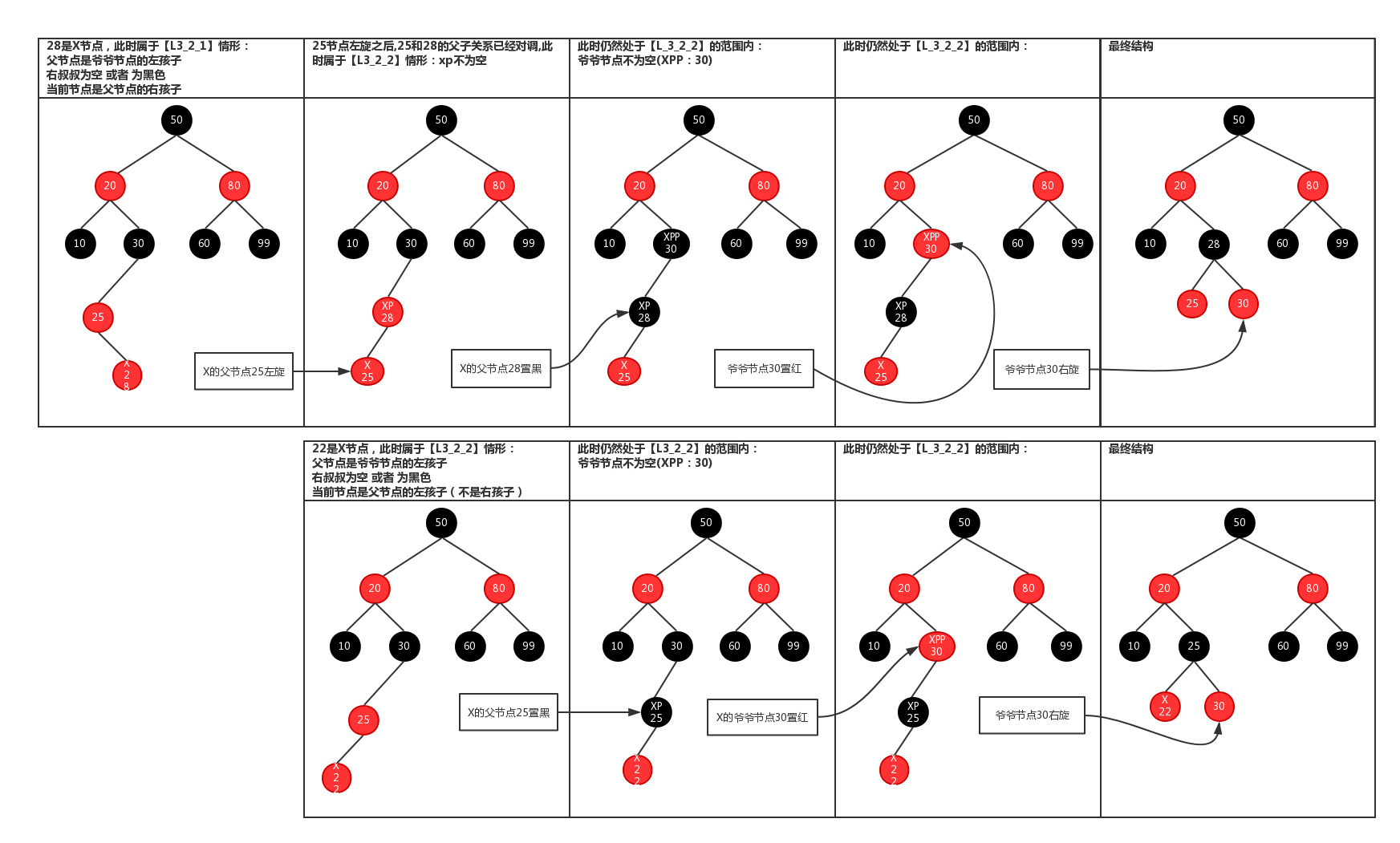
3.旋转情况2

 1 /*
 2         保证插入节点后，红黑树仍然是平衡的，代码很长，结合图看更好理解点，这样看太抽象了。但是虽然逻辑复杂，但是足以
 3         见证红黑树的高效性，因为更新树的话只是旋转操作，即改变下指针的位置，并且设置一下节点的位置就可以了
 4          */
 5         static <K, V> HashMap.TreeNode<K, V> balanceInsertion(HashMap.TreeNode<K, V> root,
 6                                                               HashMap.TreeNode<K, V> x) {
 7             //先把节点设为红色
 8             x.red = true;
 9             //定义四个节点
10             for (HashMap.TreeNode<K, V> xp, xpp, xppl, xppr; ; ) {
11                 //如果x是根节点，则把它设为黑色，并返回根节点
12                 if ((xp = x.parent) == null) {
13                     x.red = false;
14                     return x;
15                 }
16                 //如果x的父节点即xp是黑色，并且xp为根节点，则返回，什么也不做。
17                 else if (!xp.red || (xpp = xp.parent) == null)
18                     return root;
19                 //如果xp为xp父节点的左节点
20                 if (xp == (xppl = xpp.left)) {
21                     //如果xpp的右节点非空并且是红色的，那么把其设为黑色，xpp的左节点也设为黑色，xpp设为红色，并且x等于xpp
22                     if ((xppr = xpp.right) != null && xppr.red) {
23                         xppr.red = false;
24                         xp.red = false;
25                         xpp.red = true;
26                         x = xpp;
27                     }
28                     //如果xpp的右节点是空或者为黑色的话
29                     else {
30                         //如果x是xp的右节点，那么左旋xp节点，并且重新更新xp和xpp
31                         if (x == xp.right) {
32                             root = rotateLeft(root, x = xp);
33                             xpp = (xp = x.parent) == null ? null : xp.parent;
34                         }
35                         //如果x的父节点不为空，先把它设为黑色
36                         if (xp != null) {
37                             xp.red = false;
38                             //如果xp的父节点不为空，则先把xpp设为红色，然后再右旋
39                             if (xpp != null) {
40                                 xpp.red = true;
41                                 root = rotateRight(root, xpp);
42                             }
43                         }
44                     }
45                 } 
46                 //如果xp为xp父节点的右右节点
47                 else {
48                     //如果xpp的左节点非空并且是红色的话，把xppl设为黑色，xp设为黑色，xp的父节点设为红色
49                     if (xppl != null && xppl.red) {
50                         xppl.red = false;
51                         xp.red = false;
52                         xpp.red = true;
53                         x = xpp;
54                     } 
55                     //如果xpp的左节点是空或者是黑色的话
56                     else {
57                         //如果x为父节点的左节点，则右旋xp节点，并重新设置xp，xpp
58                         if (x == xp.left) {
59                             root = rotateRight(root, x = xp);
60                             xpp = (xp = x.parent) == null ? null : xp.parent;
61                         }
62                         //如果x的父节点为空，
63                         if (xp != null) {
64                             //先把其设为黑色
65                             xp.red = false;
66                             //如果xp的父节点不为空，则xpp设为红色，并左旋xpp节点
67                             if (xpp != null) {
68                                 xpp.red = true;
69                                 root = rotateLeft(root, xpp);
70                             }
71                         }
72                     }
73                 }
74             }
75         }

十、Function treeify

 1 /**
 2          * 把链表生成红黑树，返回头节点
 3          */
 4         final void treeify(HashMap.Node<K, V>[] tab) {
 5             HashMap.TreeNode<K, V> root = null;
 6 
 7             //两个指针，一个是链表的表头，一个是下一个指针
 8             for (HashMap.TreeNode<K, V> x = this, next; x != null; x = next) {
 9                 next = (HashMap.TreeNode<K, V>) x.next;
10                 x.left = x.right = null;
11 
12                 //先设定 root为头节点，parent为null，根节点为黑色，
13                 if (root == null) {
14                     x.parent = null;
15                     x.red = false;
16                     root = x;
17                 } else {
18                     K k = x.key;
19                     int h = x.hash;
20                     Class<?> kc = null;
21 
22                     //遍历红黑树
23                     for (HashMap.TreeNode<K, V> p = root; ; ) {
24                         int dir, ph;
25                         K pk = p.key;
26                         //如果当前树节点的hash > 链表节点的hash则dir值为-1
27                         if ((ph = p.hash) > h)
28                             dir = -1;
29                             //否则为1
30                         else if (ph < h)
31                             dir = 1;
32                             //如果不按照hash值比较的话，并且比较器不存在或者比较器比较的值是0的话，则把死结打开
33                         else if ((kc == null &&
34                                 (kc = comparableClassFor(k)) == null) ||
35                                 (dir = compareComparables(kc, k, pk)) == 0)
36                             dir = tieBreakOrder(k, pk);
37                         //设置一个红黑树的节点
38                         HashMap.TreeNode<K, V> xp = p;
39                         //设置节点的走向，如果dir <= 0则p为做节点，否则为右，也就是找到链表节点应该插入的位置
40                         if ((p = (dir <= 0) ? p.left : p.right) == null) {
41                             //设置链表节点的父节点
42                             x.parent = xp;
43                             if (dir <= 0)
44                                 xp.left = x;
45                             else
46                                 xp.right = x;
47                             //插入节点，并且不破坏红黑树的性质
48                             root = balanceInsertion(root, x);
49                             break;
50                         }
51                     }
52                 }
53             }
54             //设置头节点
55             moveRootToFront(tab, root);
56         }

十一、Function split

 1  /**
 2      * 树减枝，
 3      * 只有在resize的时候才调用该方法
 4      * @param map the map
 5      * @param tab 新的table
 6      * @param index 老的table的index
 7      * @param bit oldCap
 8      */
 9     final void split(HashMap<K,V> map, Node<K,V>[] tab, int index, int bit) {
10         TreeNode<K,V> b = this;
11         // Relink into lo and hi lists, preserving order
12         TreeNode<K,V> loHead = null, loTail = null;
13         TreeNode<K,V> hiHead = null, hiTail = null;
14         // 如果size很小的话则把树变成链表，用lc和hc来计数
15         int lc = 0, hc = 0;
16         // 遍历红黑树
17         for (TreeNode<K,V> e = b, next; e != null; e = next) {
18             next = (TreeNode<K,V>)e.next;
19             e.next = null;
20             // 判断将树的节点归为哪一部分
21             if ((e.hash & bit) == 0) {
22                 if ((e.prev = loTail) == null)
23                     loHead = e;
24                 else
25                     loTail.next = e;
26                 loTail = e;
27                 ++lc;
28             }
29             else {
30                 if ((e.prev = hiTail) == null)
31                     hiHead = e;
32                 else
33                     hiTail.next = e;
34                 hiTail = e;
35                 ++hc;
36             }
37         }
38 
39         //lo这部分树放入的位置，index即原先的位置
40         if (loHead != null) {
41             if (lc <= UNTREEIFY_THRESHOLD)
42                 tab[index] = loHead.untreeify(map);
43             else {
44                 tab[index] = loHead;
45                 if (hiHead != null) // (else is already treeified)
46                     loHead.treeify(tab);
47             }
48         }
49         //index+bit这部分改变了
50         if (hiHead != null) {
51             if (hc <= UNTREEIFY_THRESHOLD)
52                 tab[index + bit] = hiHead.untreeify(map);
53             else {
54                 tab[index + bit] = hiHead;
55                 if (loHead != null)
56                     hiHead.treeify(tab);
57             }
58         }
59     }

posted @ 2018-12-13 17:18 ylxn 阅读(1409) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

ylxn

时光旅客～