[bzoj1808][Ioi2007]training 训练路径——树形DP+状压DP

题目大意：

给定一个图，其中有一些铺设的边和没有铺设的边，其中铺设的边构成了一棵树，这棵树保证了每个点的度数\(\leq\) 10。未铺设的边有边权，现在要求你删去一些未铺设的边使得图中不存在偶环。

思路：

神仙题目。。。
首先可以发现如果铺设的边在树上形成了偶环，那么一定要删掉。
然后考虑放在树上会形成奇环的边。
画一画可以发现，如果两条边\((u_1,v_1)(u_2,v_2)\)它们对应的树上的路径有边相交，那么这两条边一定不能同时保留。
于是题目简化为了给一棵树添加一些边形成一颗仙人掌，并且使边权和最大。
考虑转化为有根树，把一条边挂在两个端点的lca上面，点u如果要选择一条未铺设的边\((u_0,v_0)\)，那么这条边将给\((u_0,v_0)\)在树上对应的路径打上标记，为了满足仙人掌的性质，一条边显然不可以被两条未铺设的边给标记。
于是设\(dp_{i,S}\)为第i个点集合\(S\)表示的儿子强制不考虑的最大代价。
转移的时候枚举子集，首先把那些没有强制不考虑的儿子的\(dp_{son,0}\)加入\(dp_{u,S}\)。
然后接下来我们要考虑把以这个点为lca的路径一条一条地加入，作一个类似于背包的dp。
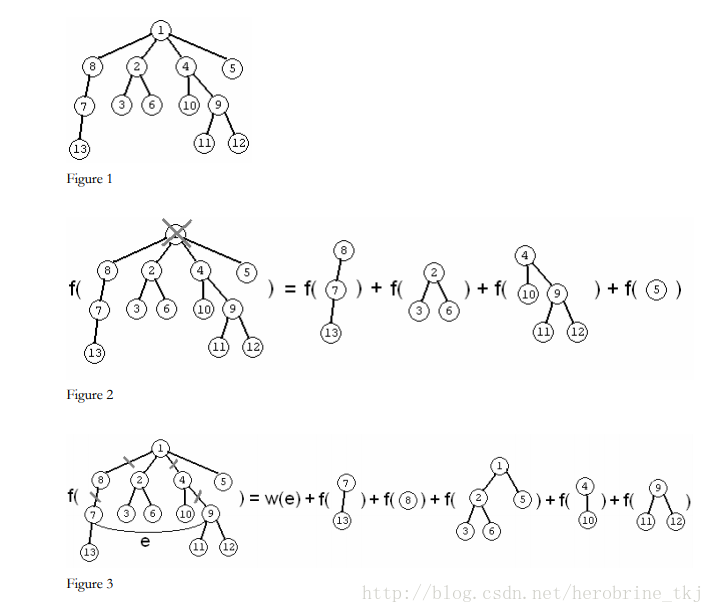
将一条路径加入时，为了保证边不被标记两次，所以我们要从这条路径不存在的状态转移过来，因为这条路径原本是不存在的，添加这条路径的同时还要加上这条路径周围的点的dp值，并且这些dp值中的边不能和这条路径有交，可以简化为将这条路径上的边全部都砍掉之后的状态。
这个图比较形象：

#include<bits/stdc++.h>

#define REP(i,a,b) for(int i=a,i##_end_=b;i<=i##_end_;++i)
#define DREP(i,a,b) for(int i=a,i##_end_=b;i>=i##_end_;--i)
#define pb push_back
typedef long long ll;

using namespace std;

void File(){
	freopen("bzoj1808.in","r",stdin);
	freopen("bzoj1808.out","w",stdout);
}

template<typename T>void read(T &_){
	T __=0,mul=1; char ch=getchar();
	while(!isdigit(ch)){
		if(ch=='-')mul=-1;
		ch=getchar();
	}
	while(isdigit(ch))__=(__<<1)+(__<<3)+(ch^'0'),ch=getchar();
	_=__*mul;
}

const int maxn=1000+10;
const int maxm=5000+10;
int n,m,st[maxn][15],dep[maxn],Log[maxn],dp[maxn][2100],id[maxn],ans;
int beg[maxn],to[maxn<<1],las[maxn<<1],cnte=1;
struct edge{
	int a,b,c;
}E[maxm];
vector<edge>G[maxn];

void add(int u,int v){
	las[++cnte]=beg[u]; beg[u]=cnte; to[cnte]=v;
	las[++cnte]=beg[v]; beg[v]=cnte; to[cnte]=u;
}

void find_ancestor(int u,int f){
	st[u][0]=f; dep[u]=dep[f]+1;
	for(int i=beg[u],v;v=to[i],i;i=las[i]){
		if(v==f)continue;
		find_ancestor(v,u);
	}
}

int lca(int x,int y){
	if(dep[x]<dep[y])swap(x,y);
	while(dep[x]>dep[y]){
		int d=Log[dep[x]-dep[y]];
		x=st[x][d];
	}
	if(x==y)return x;
	for(int d=11;d>=0;--d)
		if(st[x][d]!=st[y][d])
			x=st[x][d],y=st[y][d];
	return st[x][0];
}

void init(){
	read(n); read(m);
	REP(i,2,n)Log[i]=Log[i/2]+1;
	int u,v,w,cnt=0;
	REP(i,1,m){
		read(u); read(v); read(w);
		if(!w)add(u,v);
		else E[++cnt]=(edge){u,v,w},ans+=w;
	}
	find_ancestor(1,0);
	REP(j,1,10)REP(i,1,n)
		if((1<<j)<=dep[i]-1)
			st[i][j]=st[st[i][j-1]][j-1];
	REP(i,1,cnt){
		int an=lca(E[i].a,E[i].b);
		if((dep[E[i].a]+dep[E[i].b]-dep[an]*2)%2)continue;
		G[an].pb(E[i]);
	}
}

int sona,sonb;
int cost(int an,edge t){
	int ret=0;
	for(int u=t.a,s=0;u!=an;s=id[u],u=st[u][0])ret+=dp[u][s],sona=u;
	for(int u=t.b,s=0;u!=an;s=id[u],u=st[u][0])ret+=dp[u][s],sonb=u;
	return ret;
}

void dfs(int u,int f){
	int cnt=0;
	for(int i=beg[u],v;v=to[i],i;i=las[i]){
		if(v==f)continue;
		++cnt; id[v]=1<<(cnt-1);
		dfs(v,u);
	}
	REP(S,0,(1<<cnt)-1){
		int sum=0;
		for(int i=beg[u],v;v=to[i],i;i=las[i])
			if(!(id[v]&S))sum+=dp[v][0];
		dp[u][S]=sum;
	}
	REP(i,0,G[u].size()-1){
		sona=sonb=0;
		int c=G[u][i].c+cost(u,G[u][i]);
		DREP(S,(1<<cnt)-1,0)if(!(id[sona]&S) && !(id[sonb]&S))
			dp[u][S]=max(dp[u][S],dp[u][S|id[sona]|id[sonb]]+c);
	}
}

int main(){
	File();
	init();
	dfs(1,0);
	printf("%d\n",ans-dp[1][0]);
	return 0;
}