石子合并（区间DP）

设有N堆石子排成一排，其编号为1，2，3，…，N。

每堆石子有一定的质量，可以用一个整数来描述，现在要将这N堆石子合并成为一堆。

每次只能合并相邻的两堆，合并的代价为这两堆石子的质量之和，合并后与这两堆石子相邻的石子将和新堆相邻，合并时由于选择的顺序不同，合并的总代价也不相同。

例如有4堆石子分别为 1 3 5 2， 我们可以先合并1、2堆，代价为4，得到4 5 2， 又合并 1，2堆，代价为9，得到9 2 ，再合并得到11，总代价为4+9+11=24；

如果第二步是先合并2，3堆，则代价为7，得到4 7，最后一次合并代价为11，总代价为4+7+11=22。

问题是：找出一种合理的方法，使总的代价最小，输出最小代价。

输入格式

第一行一个数N表示石子的堆数N。

第二行N个数，表示每堆石子的质量(均不超过1000)。

输出格式

输出一个整数，表示最小代价。

数据范围

1≤N≤3001≤N≤300

输入样例：

4
1 3 5 2

输出样例：

22


题解：
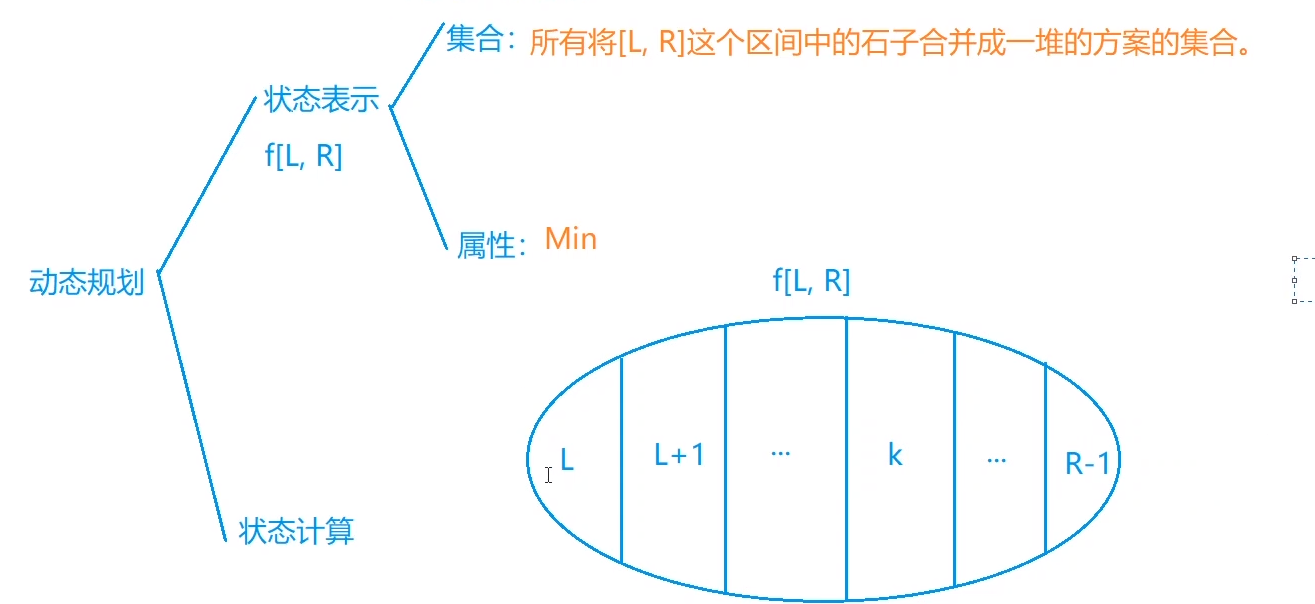
首先我们用f[L][R]来建立动态数组，该集合表示将[L,R]这个区间中的石子合并成一堆的方案集合，求出最小代价

 

 

任何一种方案都可这样表示成独立的三部分
假设L,R之间有一个值k，则该方案都可表示为左边最小+右边最小+合并两边
即L---K，K+1---R，S[R]-s[l-1]三部分

#include<bits/stdc++.h>
using namespace std;
int a[350];//最开始石子的个数
int b[350];//前缀和
int f[350][350]; //动态规划数组 
const int inf=1e9;
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
       cin>>a[i];
    for(int i=1;i<=n;i++)//前缀初始化 
       b[i]=b[i-1]+a[i]; 
    for(int len=2;len<=n;len++)//不用从1开始，为1的话就是一个集合
        for(int l=1;l+len-1<=n;l++)
        {
            int r=l+len-1;
            f[l][r]=inf;
            for(int k=l;k<r;k++)
               f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+b[r]-b[l-1]);
            
        }
    printf("%d\n",f[1][n]);     
    return 0;
}