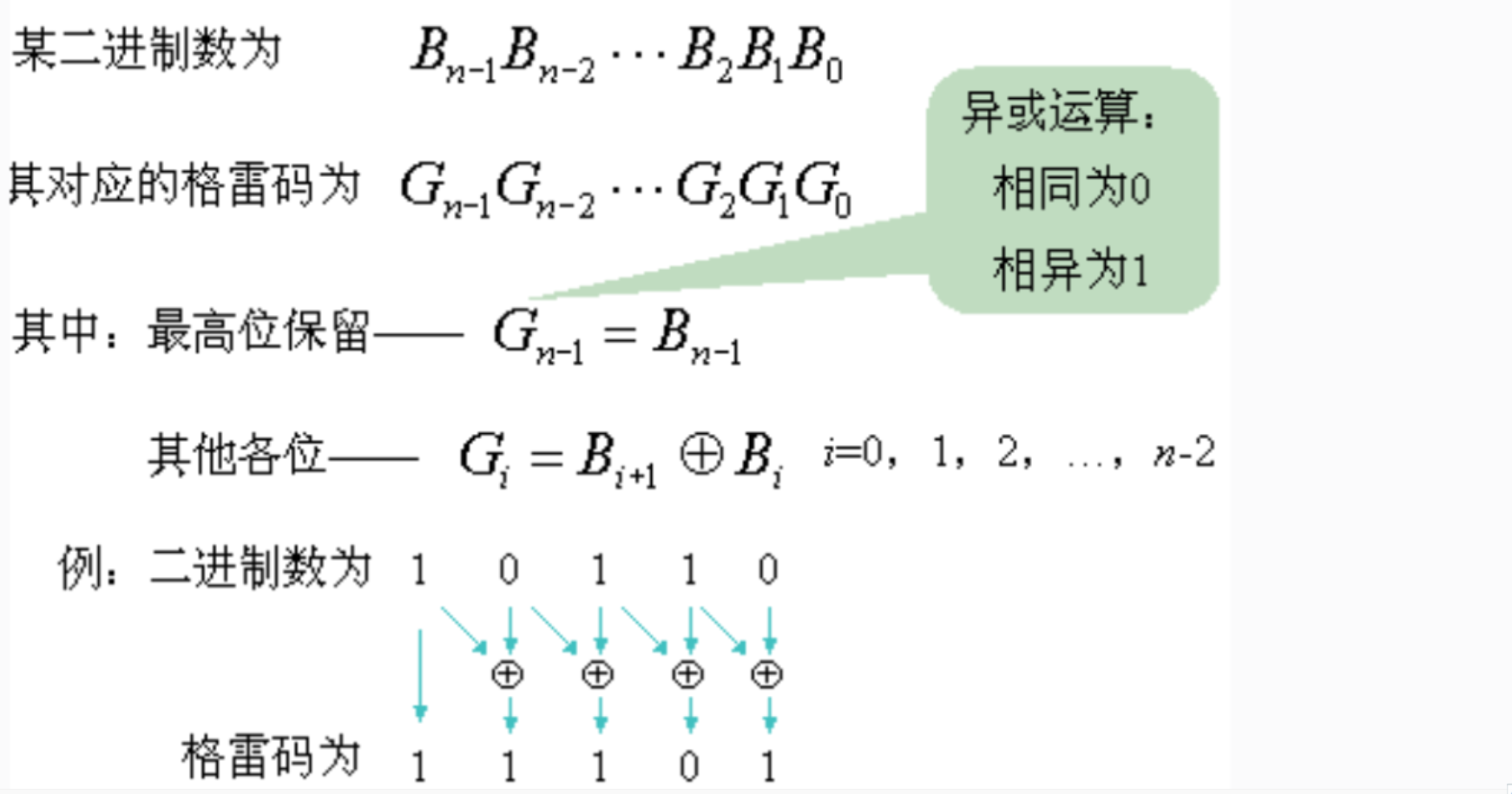
二进制格雷码与二进制自然码
---- # 二进制自然码和二进制格雷码转换以及格雷码计数器 ----
格雷码优点
格雷码的优点都来源于其固有特性:相邻两个数值之间只有1bit跳变:
- 抗干扰 ;
- 低功耗 ;
二进制自然码 -> 二进制格雷码
module bin2gry(Gry,Bin);
parameter length = 8; //以八位示例
output [length-1:0] Gry;
input [length-1:0] Bin;
reg [length-1:0] Gry;
integer i;
always @ (Bin) begin
for(i=0; i<length-1; i=i+1)
Gry[i] = Bin[i] ^ Bin[i+1];
Gry[i] = Bin[i];
end
/*另一种简单的实现方法如下:*/
// assign Gray = (Bin >> 1) ^ Bin;
endmodule
Python 获取格雷码
N = 4
binnum = [i for i in range(2**N)]
decnum = [i^(i>>1) for i in range(2**N)]
#
def get_bin (din, N):
relist = []
for n in din:
src_bin = bin(n).lstrip('0b')
len_bin = len(src_bin)
if(len_bin < N):
relist.append((N-len_bin)*'0' + src_bin)
else:
relist.append(src_bin)
return relist
#gray = []
#dbin = []
gray = get_bin(decnum, N)
dbin = get_bin(binnum, N)
#print(dbin)
#print(binnum)
#len_n = len(gray)
print ('-- gray | bin | dec --')
for i in range(0, 2**N):
print( gray[i] + ' // ' + dbin[i] + ' // ' + str(i))
#print(gray)
二进制格雷码 -> 二进制自然码

module gry2bin(Gry,Bin);
parameter length = 8;
input [length-1:0] Gry;
output [length-1:0] Bin;
reg [length-1:0] Bin;
integer i;
always @ (Gry) begin
Bin[length-1] = Gry[length-1];
for(i=length-2; i>=0; i=i-1)
Bin[i] = Bin[i+1] ^ Gry[i];
end
endmodule
可综合的格雷码计数器:
1. 通过二进制转换
下面这个例子是通过将格雷码转换为二进制,二进制再输入加法器,加法器结果再转换为格雷码。因为两次转换的组合逻辑的关系,所以如果综合器优化的不够好的话会限制计数器的速度。
当然,也可以像注释部分那样,先做一个二进制计数器再进行二进制转格雷码(滞后一个周期)。但是多消耗了1倍的寄存器数量,这在FPGA上这是可以接受的,在ASIC上就要考虑面积问题值不值得了。
如果计数器比较小,可以直接用格雷码状态机当格雷码计数器,你甚至可以画卡诺图搭一个电路。
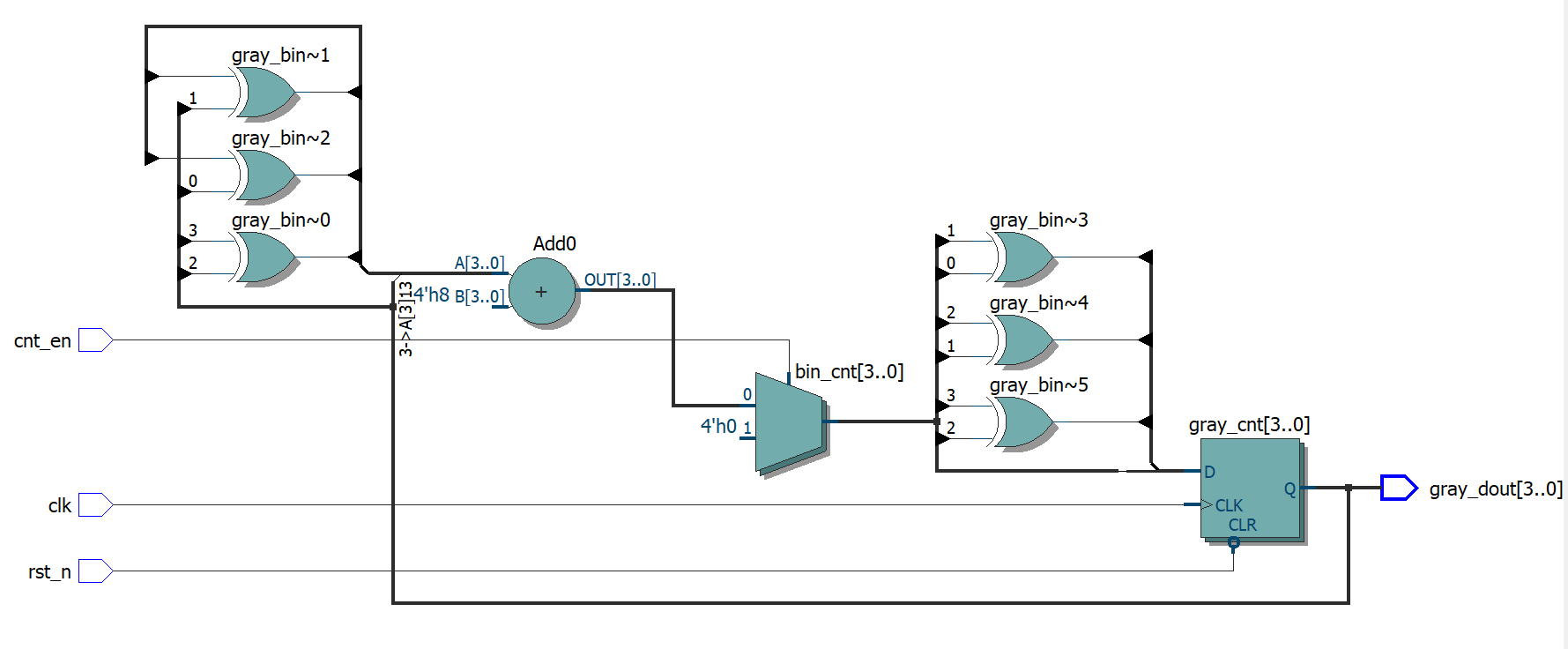
`timescale 1ns/1ps
module gray_bin_cnt #(
parameter GRAYWIDTH = 4 ,
parameter DLY = 0.5
)(
input clk ,
input rst_n ,
input cnt_en ,
//input cnt_rst ,
output wire [GRAYWIDTH-1 : 0] gray_dout
) ;
reg [GRAYWIDTH-1 : 0] gray_cnt ;
reg [GRAYWIDTH-1 : 0] bin_cnt ;
//wire [GRAYWIDTH-1 : 0] bin_cnt ;
// 十进制计数器
/*
always @(posedge clk or negedge rst_n) // 寄存器类型二进制计数器
if (rst_n == 1'b0)
bin_cnt <= #DLY{GRAYWIDTH-1{1'b0}} ;
else
bin_cnt <= #DLY bin_cnt + {{GRAYWIDTH-1{1'b0}}, 1'b1} ;
*/
//assign bin_cnt = gray_bin(1'b0, gray_cnt) + {{GRAYWIDTH-1{1'b0}}, 1'b1} ;
always @(*) begin // 组合逻辑(码制转换+加法器)
bin_cnt = {GRAYWIDTH{1'bx}} ; //@ loopback
if (cnt_en)
bin_cnt = {GRAYWIDTH{1'b0}} ;
else if (bin_cnt > {GRAYWIDTH{1'b1}} - {{GRAYWIDTH-1{1'b0}}, 1'b1}) //计数到 2^n -2
bin_cnt = {GRAYWIDTH{1'b0}} ;
else
bin_cnt = gray_bin(1'b0, gray_cnt) + {{GRAYWIDTH-1{1'b0}}, 1'b1} ; //加法器,格雷码转换二进制
end
// 格雷码计数器
always @(posedge clk or negedge rst_n)
if (rst_n == 1'b0)
gray_cnt <= #DLY 'd0 ;
else
gray_cnt <= #DLY gray_bin(1'b1, bin_cnt) ; // 二进制转换格雷码
assign gray_dout = gray_cnt ;
//function automatic [GRAYWIDTH-1:0] gray_bin (input option, input [GRAYWIDTH-1:0] din) ;
function automatic [GRAYWIDTH-1:0] gray_bin ;
input option ;
input [GRAYWIDTH-1:0] din ;
integer i ;
begin
if (option == 1'b1) //编码, 二进制->格雷码
gray_bin = (din >> 1) ^ din ;
else if (option == 1'b0) begin //解码, 格雷码->二进制
gray_bin[GRAYWIDTH-1] = din [GRAYWIDTH-1] ;
for (i = GRAYWIDTH-2; i >= 0; i = i-1)
gray_bin[i] = gray_bin[i+1] ^ din[i] ;
end
end
endfunction
endmodule
2. 通过状态机构造
状态机格雷码,注意在FPGA综合时取消优化,否则优化成了独热码,综合出来和实际编写不符。当计数器位数比较多的时候写起来比较繁琐。
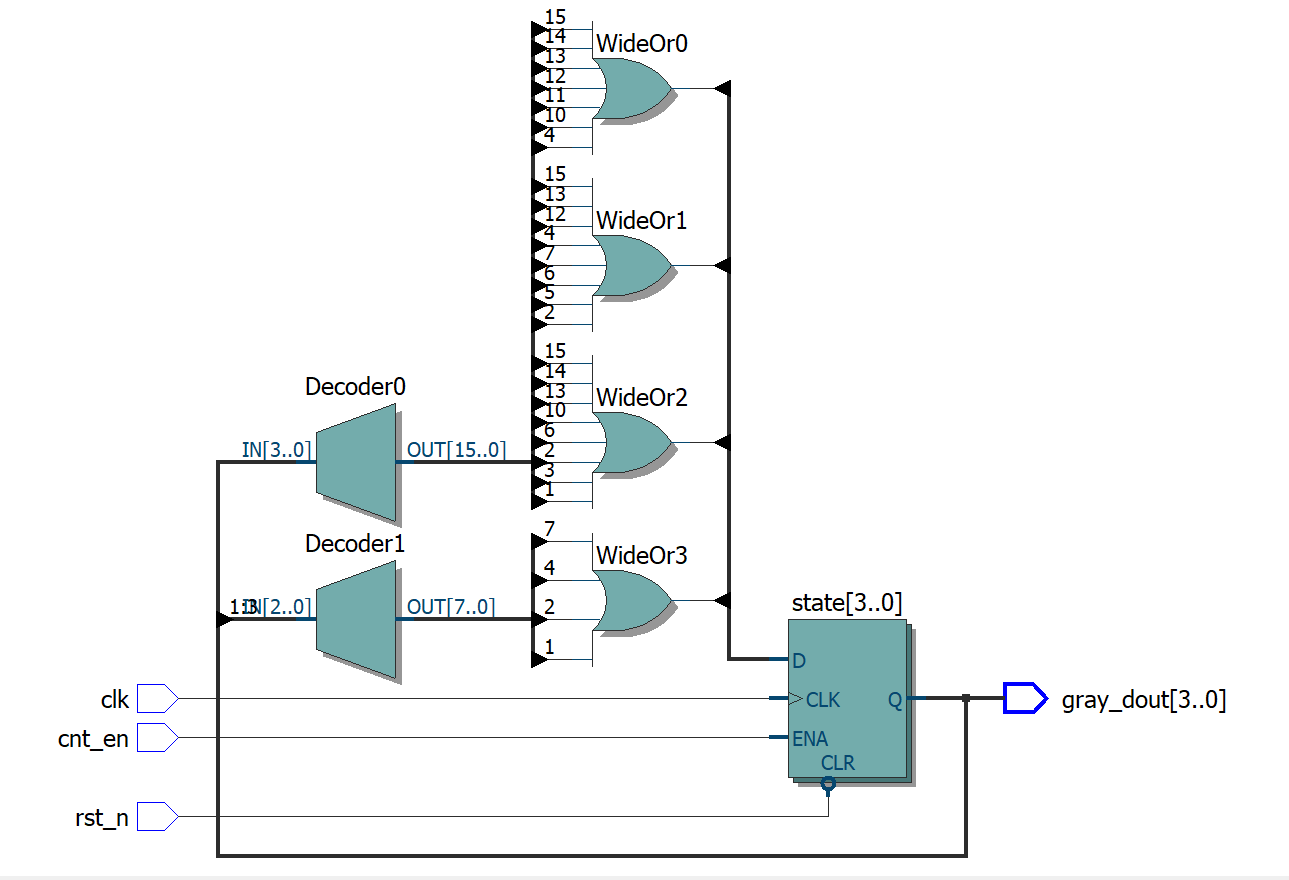
`timescale 1ns/1ps
module gray_bin_cnt #(
parameter GRAYWIDTH = 4 ,
parameter DLY = 0.5
)(
input clk ,
input rst_n ,
input cnt_en ,
//input cnt_rst ,
output wire [GRAYWIDTH-1 : 0] gray_dout
) ;
localparam [GRAYWIDTH-1 : 0]
//-- gray | bin | dec --
S0 = 4'b0000, // 0000 // 0
S1 = 4'b0001, // 0001 // 1
S2 = 4'b0011, // 0010 // 2
S3 = 4'b0010, // 0011 // 3
S4 = 4'b0110, // 0100 // 4
S5 = 4'b0111, // 0101 // 5
S6 = 4'b0101, // 0110 // 6
S7 = 4'b0100, // 0111 // 7
S8 = 4'b1100, // 1000 // 8
S9 = 4'b1101, // 1001 // 9
S10 = 4'b1111, // 1010 // 10
S11 = 4'b1110, // 1011 // 11
S12 = 4'b1010, // 1100 // 12
S13 = 4'b1011, // 1101 // 13
S14 = 4'b1001, // 1110 // 14
S15 = 4'b1000; // 1111 // 15
reg [GRAYWIDTH-1 : 0] state, next ;
always @(posedge clk or negedge rst_n)
if (rst_n == 1'b0) state <= #DLY S0 ;
else if(cnt_en) state <= #DLY next ;
always @(*) begin
next = 'bx ;
case (state)
S0 : next = S1 ;
S1 : next = S2 ;
S2 : next = S3 ;
S3 : next = S4 ;
S4 : next = S5 ;
S5 : next = S6 ;
S6 : next = S7 ;
S7 : next = S8 ;
S8 : next = S9 ;
S9 : next = S10 ;
S10 : next = S11 ;
S11 : next = S12 ;
S12 : next = S13 ;
S13 : next = S14 ;
S14 : next = S0 ;
S15 : next = S0 ;
default : next = S0 ;
endcase
end
assign gray_dout = state ;
3. 通过优化逻辑生成
参考:
(1) Quartus II, Edit -> Insert Template -> Verilog HDL -> Full Designs -> Arithmetic -> Counters -> Gray Counter
(2) 《第六届全国核仪器及其应用学术会议论文集 - 格雷码计数器的优化设计_陈晓磊,范如玉,李斌康》
二进制计数器的组合逻辑部分主要由加法器构成,一般情况下加法器是级联结构的(行波进位加法器)。基于同样的思路,格雷码应当也能有某种级联的组合逻辑构成。
如下表我们仔细观察格雷码,可以看出:
(1) 计数器最低位的翻转频率是计数时钟频率的 1/4;
(2) 当且仅当第 N 位为“1”,N-1 及以后的位都为“0”时,下一个时钟到来后第 N+1 位发生翻转 ;
基于以上两点,可以通过一个D触发器将时钟二分频,通过这个触发器和格雷码本身的触发器来组合出逻辑控制循环计数。假设格雷码计数器位数是5bit:gray [4:0] ,把时钟二分频作为辅助的最低位:gray[-1]。
可以得到如下等式:
注:gray[-1]异步置位,随时钟翻转,计数器最高位为了保证循环和次高位做了或运算逻辑。
- gray[0] = gray[0] ^ ( gray[-1] & 1'b1 )
- gray[1] = gray[1] ^ ( gray[0] & ~gray[-1] )
- gray[2] = gray[2] ^ ( gray[1] & ~gray[-1] & ~gray[0] )
- gray[3] = gray[3] ^ ( gray[2] & ~gray[-1] & ~gray[0] & ~gray[1] )
- gray[4] = gray[4] ^ ( (gray[3] | gray[4]) & ~gray[-1] & gray[0] & gray[1] & gray[2] )
| 格雷码 | 二进制 | 十进制 | 格雷码+时钟二分频 |
|---|---|---|---|
| 0 0 0 0 | 0000 | 0 | 0 0 0 0 - 1 |
| 0 0 0 1 | 0001 | 1 | 0 0 0 1 - 0 |
| 0 0 1 1 | 0010 | 2 | 0 0 1 1 - 1 |
| 0 0 1 0 | 0011 | 3 | 0 0 1 0 - 0 |
| 0 1 1 0 | 0100 | 4 | 0 1 1 0 - 1 |
| 0 1 1 1 | 0101 | 5 | 0 1 1 1 - 0 |
| 0 1 0 1 | 0110 | 6 | 0 1 0 1 - 1 |
| 0 1 0 0 | 0111 | 7 | 0 1 0 0 - 0 |
| 1 1 0 0 | 1000 | 8 | 1 1 0 0 - 1 |
| 1 1 0 1 | 1001 | 9 | 1 1 0 1 - 0 |
| 1 1 1 1 | 1010 | 10 | 1 1 1 1 - 1 |
| 1 1 1 0 | 1011 | 11 | 1 1 1 0 - 0 |
| 1 0 1 0 | 1100 | 12 | 1 0 1 0 - 1 |
| 1 0 1 1 | 1101 | 13 | 1 0 1 1 - 0 |
| 1 0 0 1 | 1110 | 14 | 1 0 0 1 - 1 |
| 1 0 0 0 | 1111 | 15 | 1 0 0 0 - 0 |
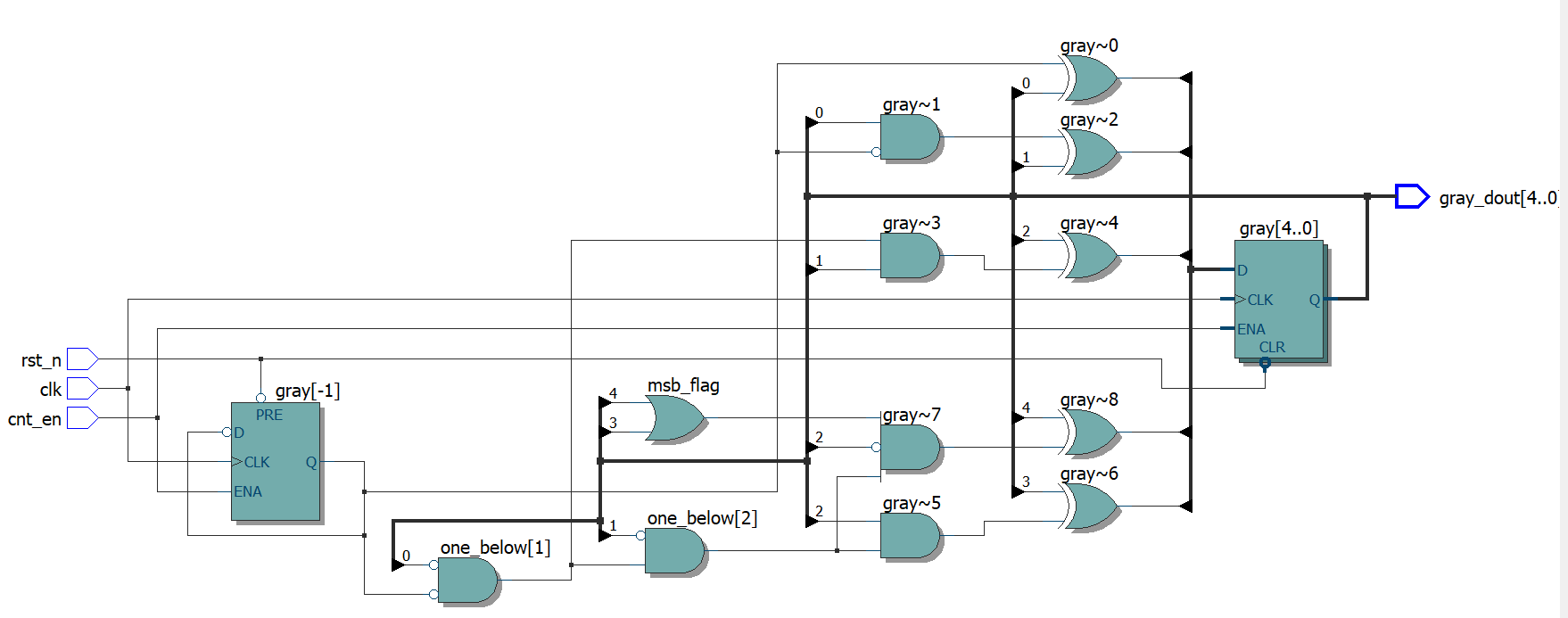 |
`timescale 1ns/1ps
module gray_bin_cnt #(
parameter GRAYWIDTH = 5 ,
parameter DLY = 0.5
)(
input clk ,
input rst_n ,
input cnt_en ,
//input cnt_rst ,
output wire [GRAYWIDTH-1 : 0] gray_dout
) ;
reg [GRAYWIDTH-1:-1] gray ;
reg [GRAYWIDTH-2:-1] one_below ;
wire msb_flag ;
integer i, j ;
//部分级联的组合逻辑
always @(*) begin
one_below[-1] = 1'b1 ;
for (j = 0; j <= GRAYWIDTH-2; j = j + 1)
one_below[j] = one_below[j-1] & ~gray[j-1] ;
end
assign msb_flag = gray[GRAYWIDTH-1] | gray[GRAYWIDTH-2];
always @(posedge clk or negedge rst_n)
if (rst_n == 1'b0)
gray <= {{GRAYWIDTH{1'b0}}, 1'b1} ;
else if (cnt_en) begin
gray[-1] <= ~gray[-1] ;
for (i = 0; i < GRAYWIDTH-1; i = i + 1)
gray[i] <= gray[i] ^ (gray[i-1] & one_below[i-1]) ;
gray[GRAYWIDTH-1] <= gray[GRAYWIDTH-1] ^ (msb_flag & one_below[GRAYWIDTH-2] ) ;
end
assign gray_dout = gray[GRAYWIDTH-1:0] ;
endmodule
4. 总结
一般为了简单推荐二进制转换的方式,不易出错。
尽管优化逻辑生成的格雷码计数器相对省资源和逻辑简单,但是当位数太大就不推荐此方式了,二进制转换的方式加法器部分可以用超前进位方式换取速度(感觉拆分行波进位加法器也可以)。
CDC书籍:
https://github.com/yllinux/blogPic/blob/master/doc/CummingsSNUG2008Boston_CDC.pdf
参考:https://blog.csdn.net/gordon_77/article/details/79489548
https://www.cnblogs.com/ZcsTech/p/3500207.html
https://zhuanlan.zhihu.com/p/130732799


 浙公网安备 33010602011771号
浙公网安备 33010602011771号