数据结构之红黑树-动图演示

红黑树是比较常见的数据结构之一，在Linux内核中的完全公平调度器、高精度计时器、多种语言的函数库(如,Java的TreeMap)等都有使用。

在学习红黑树之前，先来熟悉一下二叉查找树。

二叉查找树(Binary Search Tree)

二叉查找树，它有一个根节点，且每个节点下最多有只能有两个子节点，左子节点的值小于其父节点，右子节点的值大于其父节点。

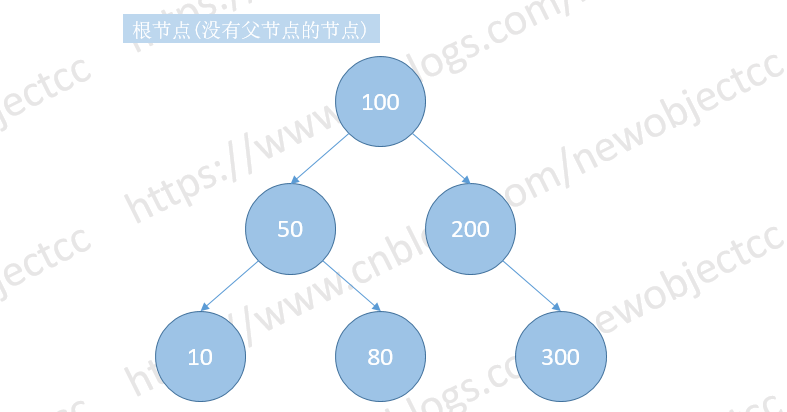
插入节点

从根节点向下查找，当新插入节点大于比较的节点时，新节点插入到比较节点的右侧，当小于比较的节点时，插入到比较节点的左侧，一直向下比较大小，找到要插入元素的位置并插入元素。

如图: 依次插入节点[100,50,200,80,300,10]

伪代码(来源Java TreeMap，有省略和修改):

void put(K key, V value) {
     if (root == null) {
        root = new Node<>(key, value, null); 
        return;
    }       
    Node<K,V> t = root; 
    int cmp; // 比较结果    
    Node<K,V> parent;  
    Comparable<? super K> k = (Comparable<? super K>) key;
    do {
        parent = t;
        cmp = k.compareTo(t.key);
        if (cmp < 0)
            t = t.left;
        else if (cmp > 0)
            t = t.right;
        else
            return; // 节点存在直接返回
    } while (t != null);
Node&lt;K,V&gt; e = <span class="hljs-keyword">new</span> Node&lt;&gt;(key, value, parent);
<span class="hljs-keyword">if</span> (cmp &lt; <span class="hljs-number">0</span>){
     parent.left = e;
}<span class="hljs-keyword">else</span>{
   parent.right = e;  
}  

}

查找节点

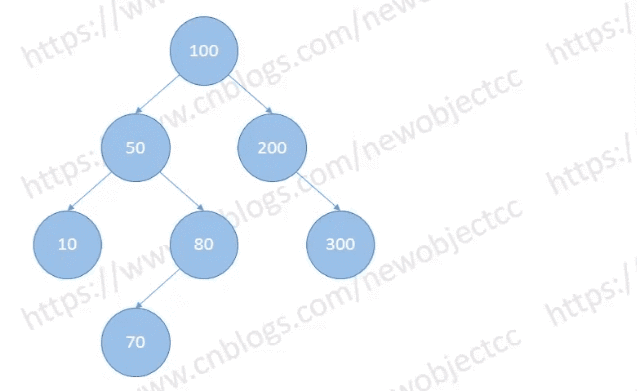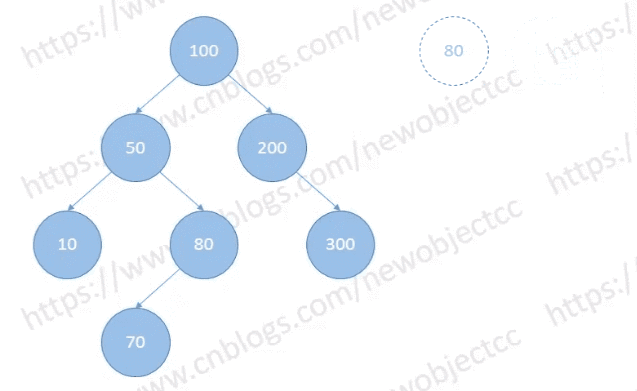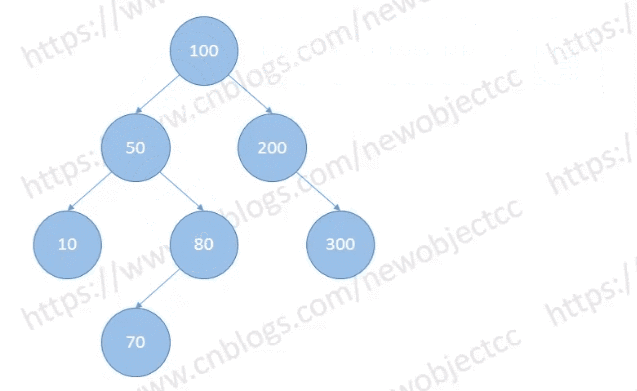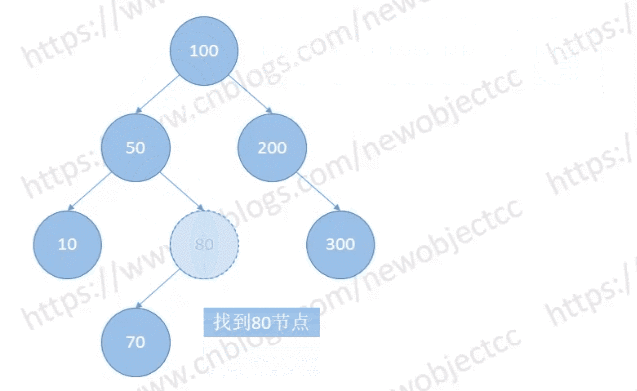
从根节点开始向下查找，当查找节点大于比较的节点时，向右查找，当小于当前比较节点时，就向左查找。一直向下查找，直到找到对应的节点或到终点查找结束。

如图: 查找节点[80]

伪代码(来源Java TreeMap，有省略和修改):

Node<K,V> getNode(Object key) {
    Comparable<? super K> k = (Comparable<? super K>) key;
    Node<K,V> p = root;
    while (p != null) {
        int cmp = k.compareTo(p.key);
        if (cmp < 0)
            p = p.left;
        else if (cmp > 0)
            p = p.right;
        else
            return p;
    }
    return null;
}

删除节点

删除节点首先要查找要删除的节点，找到后执行删除操作。

删除节点的节点有如下几种情况：

1. 删除的节点有两个子节点
2. 删除的节点有一个子节点
3. 删除的节点没有子节点

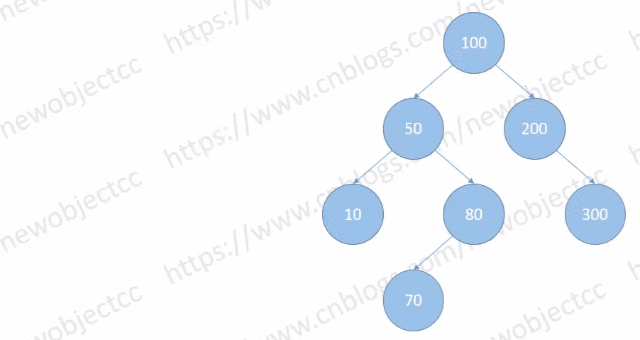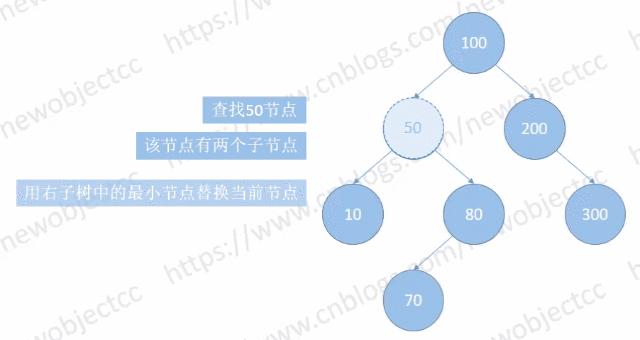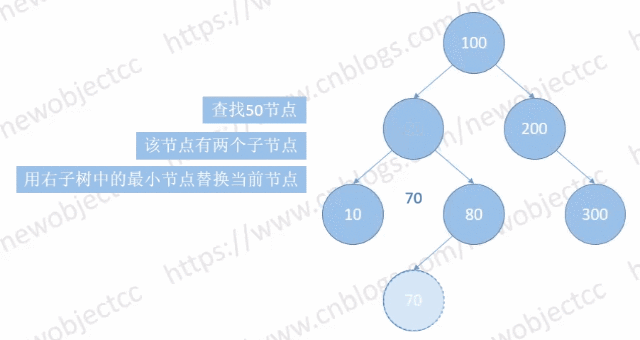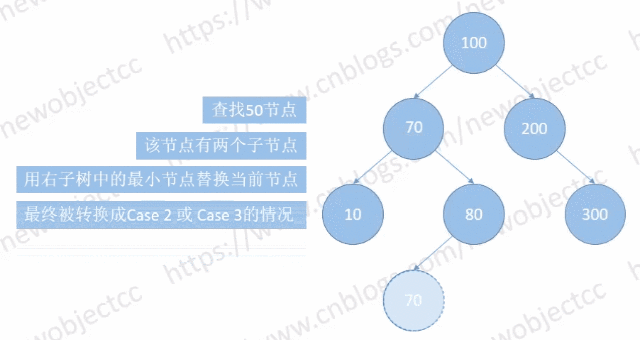
Case 1：

该种情况下，涉及到节点的“位置变换”，用右子树中的最小节点替换当前节点。从右子树一直 left 到 NULL。最后会被转换为 Case 2 或 Case 3 的情况。

所以对于删除有两个孩子的节点，删除的是其右子树的最小节点，最小节点的内容会替换要删除节点的内容。

如图:删除节点[50]

Case 2：

有一个子节点的情况下，将其父节点指向其子节点，然后删除该节点。

如图:删除节点[200]

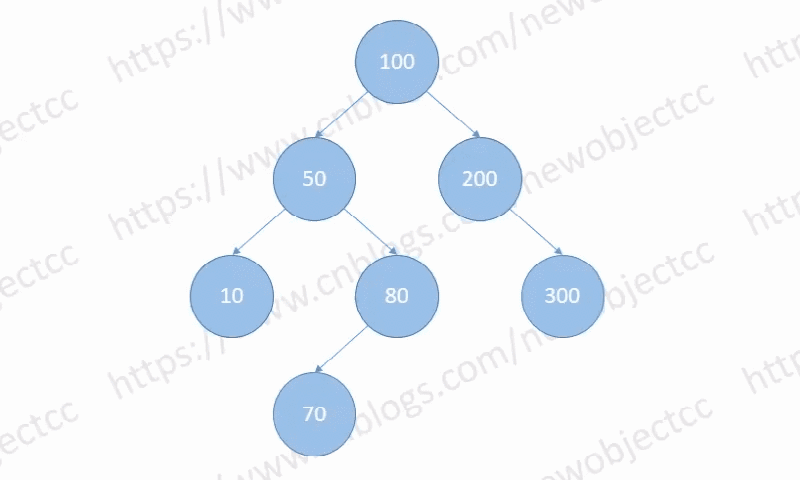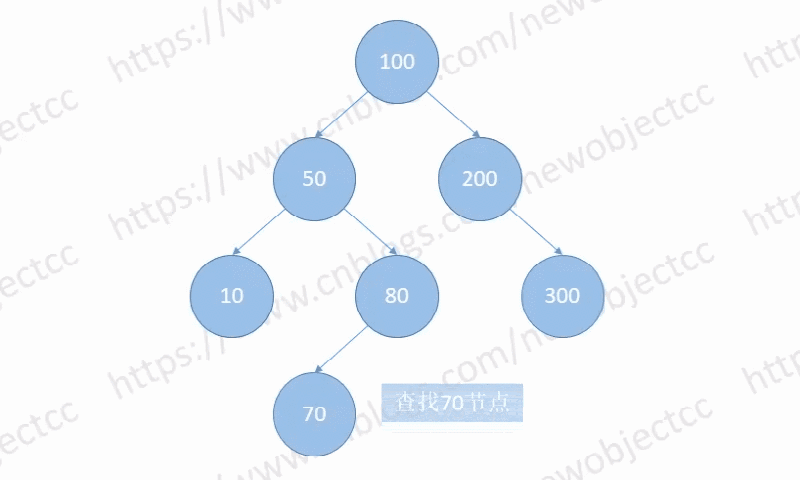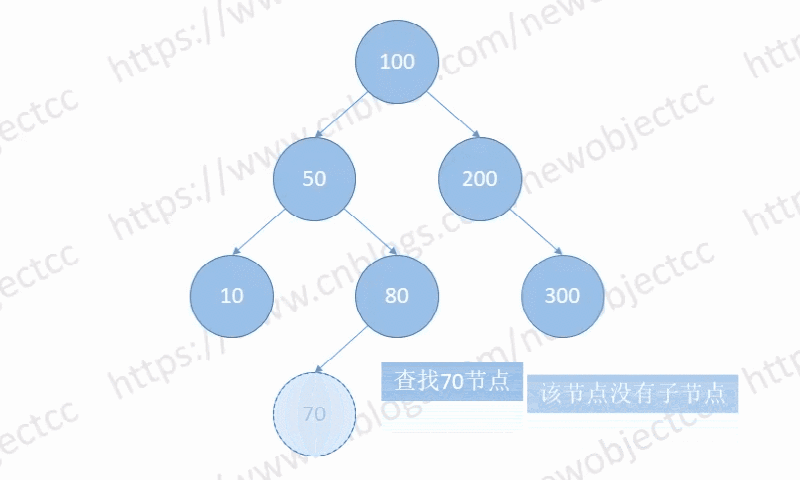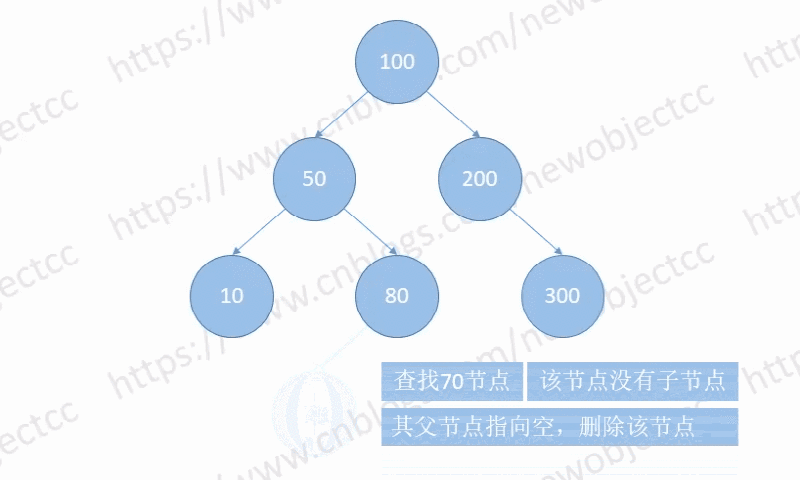
Case 3：

在没有子节点的情况，其父节点指向空，然后删除该节点。

如图:删除节点[70]

伪代码(来源Java TreeMap，有省略和修改):

Node remove(Object key) {
    // 查找节点(参考上面查找代码)
    Node<K,V> p = getNode(key); 
 <span class="hljs-comment">// 节点变换。 p 有两个子节点，将其转换为删除后继节点</span>
<span class="hljs-keyword">if</span> (p.left != <span class="hljs-keyword">null</span> &amp;&amp; p.right != <span class="hljs-keyword">null</span>) {
    Entry&lt;K,V&gt; s = t.right;
    <span class="hljs-keyword">while</span> (s.left != <span class="hljs-keyword">null</span>){
        s = s.left;
    }
    p.key = s.key;
    p.value = s.value;
    p = s;
} 

Entry&lt;K,V&gt; replacement = (p.left != <span class="hljs-keyword">null</span> ? p.left : p.right);
<span class="hljs-comment">// p 有一个子节点</span>
<span class="hljs-keyword">if</span> (replacement != <span class="hljs-keyword">null</span>) {
    replacement.parent = p.parent;
    <span class="hljs-keyword">if</span> (p.parent == <span class="hljs-keyword">null</span>){
        root = replacement;
    }  <span class="hljs-keyword">else</span> <span class="hljs-keyword">if</span> (p == p.parent.left){
        p.parent.left  = replacement;
    } <span class="hljs-keyword">else</span>{
        p.parent.right = replacement;
    }
    p.left = p.right = p.parent = <span class="hljs-keyword">null</span>;

} <span class="hljs-keyword">else</span> <span class="hljs-keyword">if</span> (p.parent == <span class="hljs-keyword">null</span>) { <span class="hljs-comment">// 根节点</span>
   
     root = <span class="hljs-keyword">null</span>;
} <span class="hljs-keyword">else</span> { <span class="hljs-comment">//  p 没有子节点</span>
   
     <span class="hljs-keyword">if</span> (p == p.parent.left){
        p.parent.left = <span class="hljs-keyword">null</span>;
    } <span class="hljs-keyword">else</span> <span class="hljs-keyword">if</span> (p == p.parent.right){
        p.parent.right = <span class="hljs-keyword">null</span>;
    }
    p.parent = <span class="hljs-keyword">null</span>;   
} 
<span class="hljs-keyword">return</span> p;

}

树的优势

我们知道，有序数组删除或插入数据较慢（向数组中插入数据时，涉及到插入位置前后数据移动的操作），但根据索引查找数据很快，可以快速定位到数据，适合查询。而链表正好相反，查找数据比较慢，插入或删除数据较快，只需要引用移动下就可以，适合增删。

而二叉树就是同时具有以上优势的数据结构。

该树缺点

上面的树是非平衡树，由于插入数据顺序原因，多个节点可能会倾向根的一侧。极限情况下所有元素都在一侧，此时就变成了一个相当于链表的结构。

如图:依次插入节点[100,150,170,300,450,520 ...]

这种不平衡将会使树的层级增多（树的高度增加），查找或插入元素效率变低。

那么只要当插入元素或删除元素时还能维持树的平衡，使元素不至于向一端严重倾斜，就可以避免这个问题。

到此，红黑树闪亮登场， 红黑树就是一种平衡二叉树。

红黑树（Red Black Tree）

红黑树是一种平衡二叉树，遵守如下规则来保证红黑树的平衡，保证每个节点在它左边的后代数目和在它右边的后代数目应该是大致相等（最长路径也不会超过最短路径的2倍）。

红黑树的规则

红黑树是在二叉查找树基础之上再遵循如下规则的树

1. 每个节点颜色不是黑色就是红色
2. 根节点一定为黑色
3. 两个红色节点不能相邻（红色节点的子节点一定是黑色）
4. 从任意节点到叶子节点的每条路径包含的黑色节点数目相同（黑色高度）
5. 每个叶子节点(NULL节点，空节点)是黑色

当插入或删除节点时，必须要遵守红黑树的规则，根据这些规则来决定是否需要改变树的结构或节点颜色，使其达到平衡。

查找节点并不影响树的平衡，所以红黑树的节点查找和二叉查找树的操作是一样的（请参考二叉查找树）。

如图: 红黑树 - 依次插入节点[100,200,300,400,500,600,700,800]

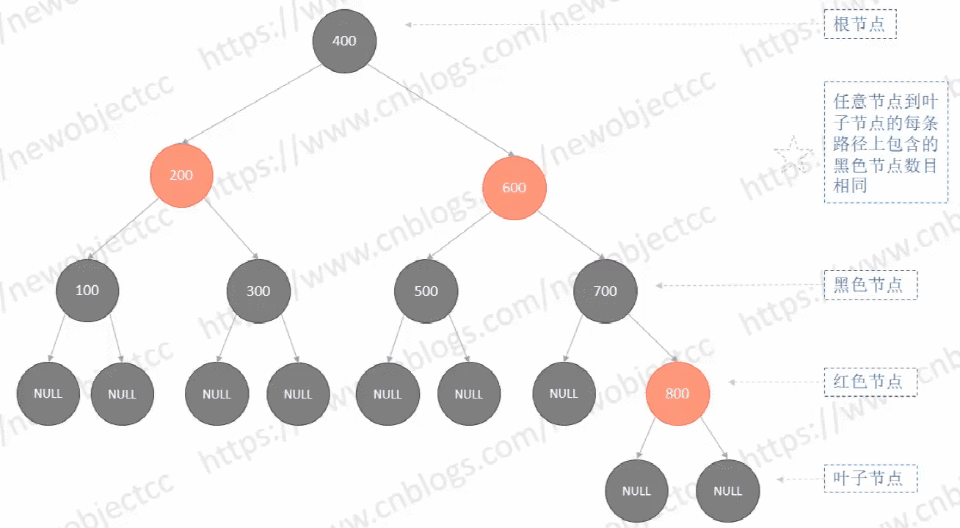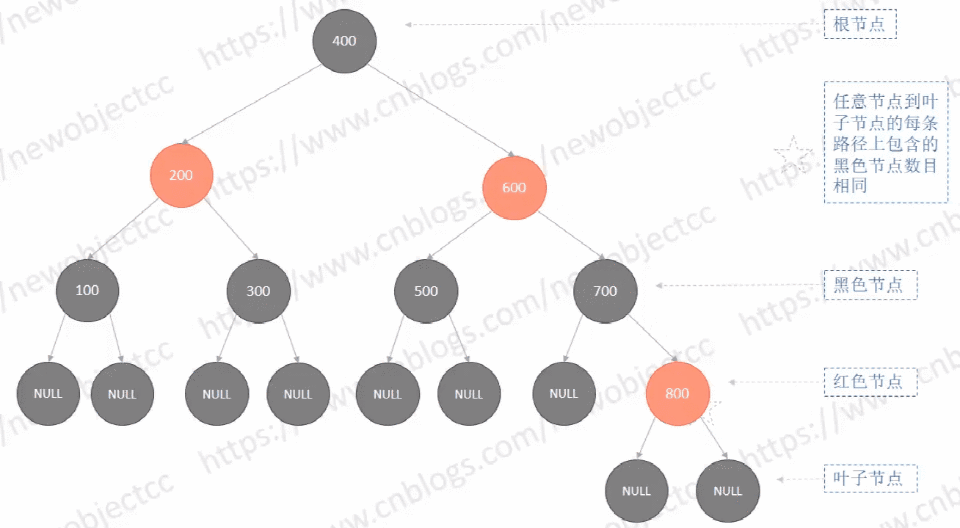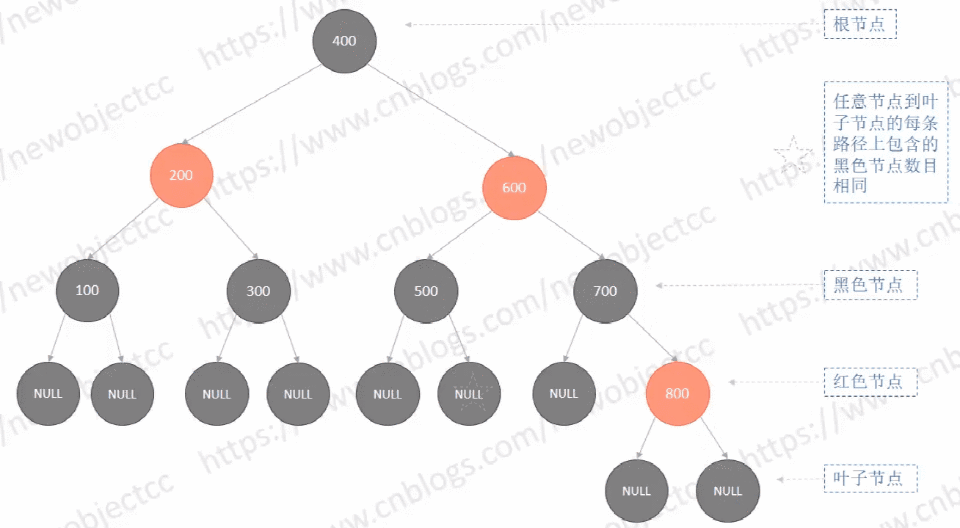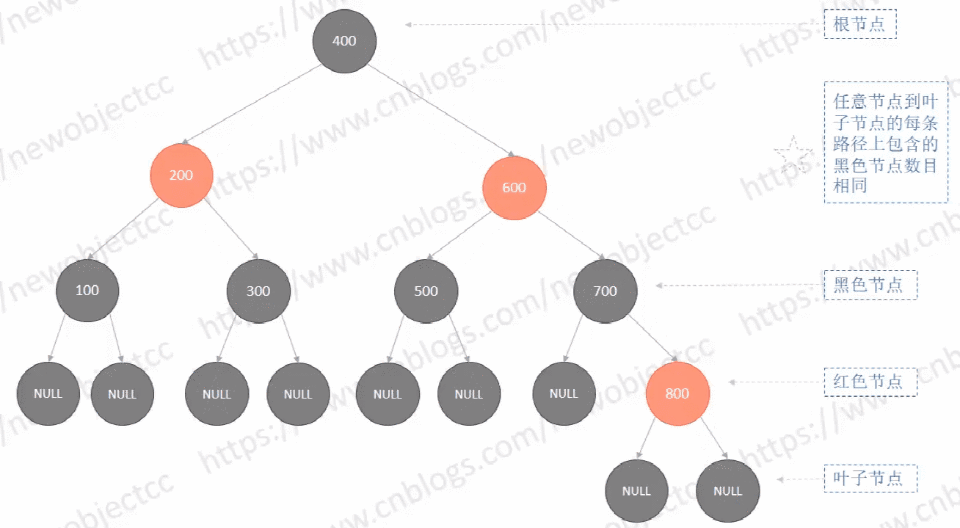
最终树的结构是大致平衡的，不像二叉查找树那样偏向一侧。

了解变色和旋转

如果新插入元素或删除元素后，红黑树的规则被破坏，这时需要对树进行调整来重新满足红黑树规则。调整有变色和旋转（左旋或右旋）两种方式，接下来分别了解这两种方式：

• 变色

通过改变节点颜色修正红黑树，节点由红变黑或黑变红

• 旋转

通过改变节点的位置关系修正红黑树

如图: 以右旋为例

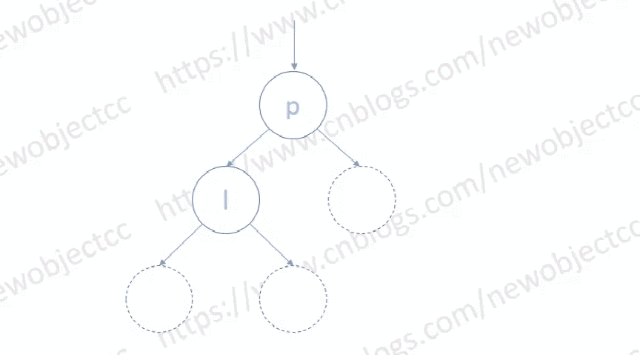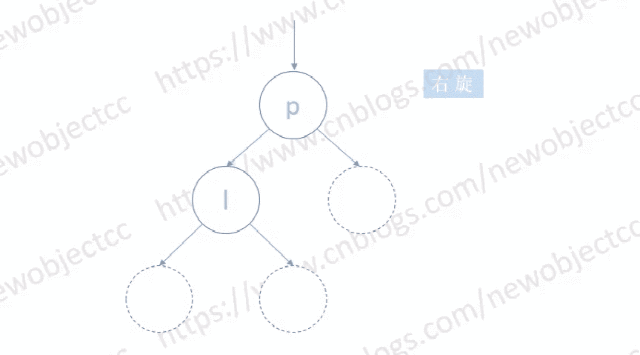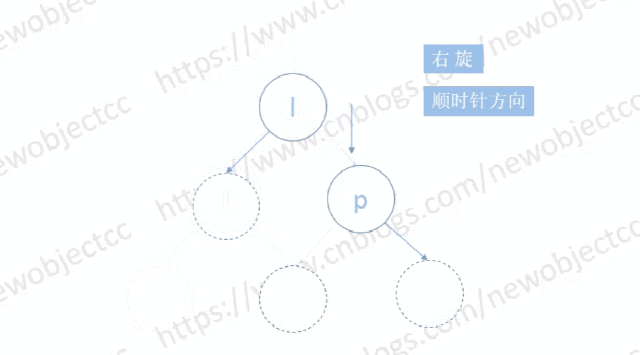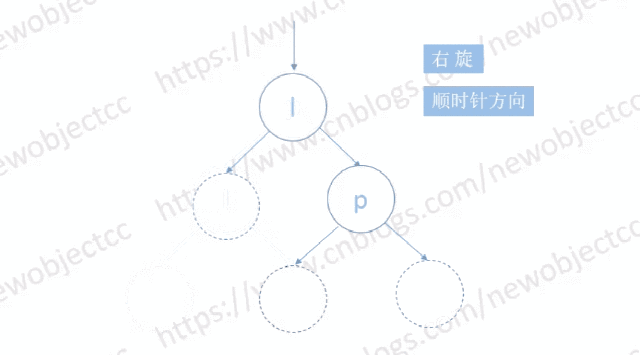
左旋则与右旋对称，为逆时针旋转。

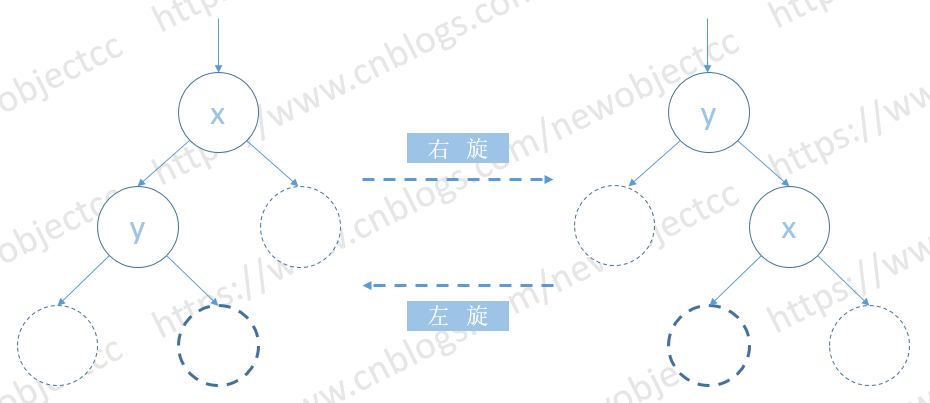
图中空节点位置可以是多个节点构成的子树，也可以是一个具体节点。

右旋(来源Java TreeMap):

private void rotateRight(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> l = p.left;
        p.left = l.right;
        if (l.right != null) 
            l.right.parent = p;
        l.parent = p.parent;
        if (p.parent == null)
            root = l;
        else if (p.parent.right == p)
            p.parent.right = l;
        else p.parent.left = l;
        l.right = p;
        p.parent = l;
    }
}

左旋(来源Java TreeMap):

private void rotateLeft(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> r = p.right;
        p.right = r.left;
        if (r.left != null)
            r.left.parent = p;
        r.parent = p.parent;
        if (p.parent == null)
            root = r;
        else if (p.parent.left == p)
            p.parent.left = r;
        else
            p.parent.right = r;
        r.left = p;
        p.parent = r;
    }
}

红黑树的插入和删除节点请看下一篇： 数据结构之红黑树-动图演示(下) - 更新中 ...