谈谈回文子串
引子
1. 先讲个歪果仁的故事,在庞贝古城的废墟中,有一座名为赫库兰尼姆的城市,在这个遗迹中人们发现一块石碑,石碑上写着一个非常有趣的拉丁串:sator arepo tenet opera rotas翻译到中文大概意思是:一个叫做arepo的耕作者,他用力地把着车轮。

这样排列一下,从上下左右读都是一样的,歪果仁挺会完的。
2. 让我印象更深刻的是高中老师给我们讲的一个故事,有一天宋代著名文学家苏轼和他的妹妹苏小妹正在荡舟湖上,欣赏着风景,忽然有人呈上秦少游捎来的一封书信。打开一看,原来是一首别出心裁的回文诗:
苏小妹看罢微微一笑,立即看出其中的奥秘,读出了这首叠字回文诗:
静思伊久阻归期,
久阻归期忆别离;
忆别离时闻漏转,
时闻漏转静思伊。
苏小妹被丈夫的一片痴情深深感到动,心中荡起无限相思之情。面对一望无际的西湖美景,便仿少游诗体,也作了一首回环诗,遥寄远方的亲人:
采莲人在绿杨津,
在绿杨津一阕新;
一阕新歌声漱玉,
歌声漱玉采莲人。
苏东坡在一旁深为小妹的过人才智暗暗高兴,他也不甘寂寞,略加沉吟,便提笔写了如下一首:
赏花归去马如飞,
去马如飞酒力微;
酒力微醒时已暮,
醒时已暮赏花归。
苏氏兄妹也派人将他们的诗作送与秦少游。
老师讲完这个故事我就感觉古人写诗都是开挂的,这些诗倒过来还是一首完整诗,都是叠字回文诗。
故事是好故事,可是本人不太会讲故事,关于回文的趣事还有很多,想看故事的可以自己去找。
正文
问题:给你一个字符串长度为n,现在让你求出这个字符串最长回文子串的长度。
解法一:
纯暴力,找出这个字符串的所有子串,然后判断每个子串是否是回文串,维护更新最大的长度即可。空间复杂度O(1),时间复杂度O(n^3)。
解法二:
解法一实在是太暴力了,换个思路暴力,长度为奇数的回文串以中间字符为对称轴成轴对称,长度为偶数的回文串以中间空隙为对称轴成轴对称。那么我们不就可以枚举对称轴,同时比较左右两边的字符,直到左右两边出现的字符不同或者达到边界。枚举的过程中维护更新最大长度即可。空间复杂度O(1),时间复杂度O(n^2)。虽然也很暴力,但是比解法一比起来就好太多了。
解法三:
上面的解法都有很多重复计算的地方,我们存储已计算的内容,之后直接使用,那么就能进一步优化时间复杂度,这是典型的空间换时间的思路。解法二有一些值得学习的地方,但是还存在问题,除了重复计算,还有就是分奇偶,相当于要进行两次处理。
1. 先解决分奇偶的问题
为了避免分奇偶讨论,我们可以对原字符串进行一些处理,在原字符串中插入一些字符:
abcba 转化为 #a#b#c#b#a#
abccba 转化为 #a#b#c#c#b#a#
进行上面的处理后整个字符串的长度肯定为奇数,而且,不改变原串的回文结构。要保证这点我们选择插入的字符一定要是原串中不存在的。
2. 避免重复计算
我们先来看看解法二中哪里就有重复计算了
a b a b a
0 1 2 3 4
以1为对称轴时,我们已经遍历了aba,当以2为对称轴的时候其实又遍历了一遍aba,左边的子串aba被遍历了两次。其实遍历过的部分只要提取出有用的部分保持下来就无需再遍历了。
回文半径:最左或最右位置的字符与其对称轴的距离。
现在申请一个数组LR,LR[i]表示以i为对称轴的回文半径。
| # | a | # | b | # | c | # | b | # | a | # | |
| i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| LR | 1 | 2 | 1 | 2 | 1 | 6 | 1 | 2 | 1 | 2 | 1 |
| LR-1 | 0 | 1 | 0 | 1 | 0 | 5 | 0 | 1 | 0 | 1 | 0 |
我们发现,max(LR-1)即时我们要求的结果。
现在问题就转化为:怎么快速的得到LR数组了。
现在再约定一个值MaxRight,MaxRight表示当前所遍历到的所有回文子串中,最靠右的索引。
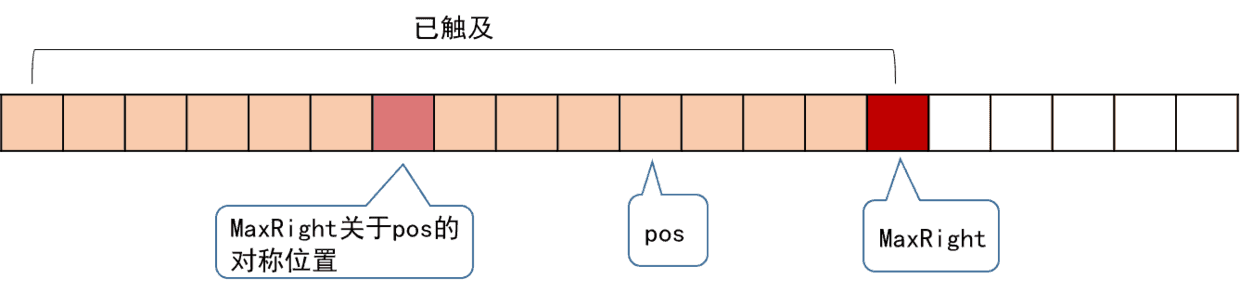
pos为对称轴,从左往右地遍历字符串来求RL,假设当前访问到的位置为i,即要求RL[i],在对应上图,i必然是在pos大(pos和pos前的已经求解完成)。但是i和MaxRight的相对关系并不确定。
1. i在MaxRight的左边
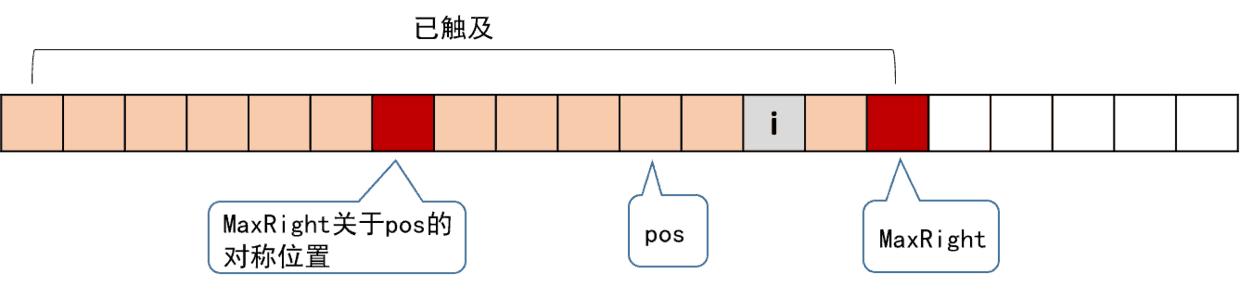
从图上观察,我们可以利用已知部分来初步确定下LR[i]的值,假设i关于pos的对称点时j,现在我们来梳理一下已知量:LR[j],MaxRight,pos,其中j = 2*pos - i.

假设LR[j]比较短,整体就包含在红色区间内,那么由于对称性LR[i]≥LR[j].

现在RL[j]不完全包含在红色区间内,上面JL等于JR关于j对称,IL等于JR、JL等于IR关于pos对称,那么IL等于IR,也就是说LR[i]≥MaxRight-i.
通过上面两种情况的讨论,求解LR[i]的使用利用了已知部分的信息,避免了重复遍历,我们可以得到LR[i] ≥ min(LR[j], MaxRight-i]),这个就很强。
对于后面还不确定的长度继续遍历即可,此时遍历的都是之前没有遍历过的。
2. i在MaxRight的右边
这种无需利用已知信息(也用不上),直接遍历未知部分,更新MaxRight和pos即可。
一句话总结一下,上面我们在干嘛,怎么就优化了复杂度:维护MaxRight和pos,在更新RL[i]时避免了重复计算。
code:
1 const int MAXN = 1000010; 2 char Ma[2*MAXN]; // 插入字符后的原数组 3 int LR[2*MAXN]; // LR 4 int MR = 0; // MaxRight 5 int pos = 0; // pos 6 7 void Manacher(char s[], int len) 8 { 9 int l = 0; 10 11 // 处理原数组 12 Ma[l++] = 'S'; 13 Ma[l++] = '#'; 14 for (int i = 0; i < len; ++i) { 15 Ma[l++] = s[i]; 16 Ma[l++] = '#'; 17 } 18 Ma[l] = 0; 19 20 for (int i = 0; i < l; ++i) { 21 22 // 利用已知信息,避免重复计算 23 LR[i] = MR > i ? min(LR[2*pos-i], MR-i) : 1; 24 25 // 继续找 26 while (Ma[i+LR[i]] == Ma[i-LR[i]]) { 27 ++LR[i]; 28 } 29 30 // 更新MaxRight pos 31 if (i + LR[i] > MR) { 32 MR = i +LR[i]; 33 pos = i; 34 } 35 } 36 }
算法空间复杂度O(n),时间复杂度O(n),这个稍微解释下,虽然代码里面是两重循环,由于内层的循环只对尚未遍历的部分进行,因此对于每一个字符而言,只会进行访问一次。


