面试题9：斐波那契数列

题目链接：http://ac.jobdu.com/problem.php?pid=1387

思路：下面是斐波那契额数列的数学公式

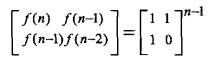
利用上面的公式和矩阵快速幂可以在logn的时间复杂度内解决问题。

注：具体矩阵快速幂的思想是怎么样的，可以自己搜索，网上资料很多。

这题当然可以暴力，然后将所有的结果存下来，毕竟只有70组数据，不过这样未免！！！

code:

// 斐波那契额数列

#include <cstdio>
#include <cstring>
using namespace std;
const int M = 2;
const int MOD = 1000000007;
typedef long long LL;
LL ans[M][M];
LL tmp[M][M];

// 矩阵乘法
void matrixMul(LL mat1[M][M], LL mat2[M][M])
{
    LL mat3[M][M];
    for (int i = 0; i < M; ++i)
    {
        for (int j = 0; j < M; ++j)
        {
            mat3[i][j] = 0;
            for (int k = 0; k < M; ++k)
                mat3[i][j] += mat1[i][k] * mat2[k][j];
        }
    }
    memcpy(mat1, mat3, sizeof(mat3));
}

// 矩阵快速幂
void matrixQuickMod(int n)
{
    tmp[0][0] = 1;
    tmp[0][1] = 1;
    tmp[1][0] = 1;
    tmp[1][1] = 0;

    // 将ans处理成单位矩阵
    memset(ans, 0, sizeof(ans));
    for (int i = 0; i < M; ++i) ans[i][i] = 1;

    while (n)
    {
        if (n & 1) matrixMul(ans, tmp);        // 当n为奇数时，跟新ans
        n >>= 1;
        matrixMul(tmp, tmp);    // 当n为偶数时跟新tmp
    }
}

int main()
{
    int n;
    while (scanf("%d", &n) != EOF)
    {
        matrixQuickMod(n - 1);    
        printf("%lld\n", ans[0][0]);
    }
    return 0;
}