回归分析 | R语言回归算法、模型诊断
一、回归算法
1.1 一元线性回归
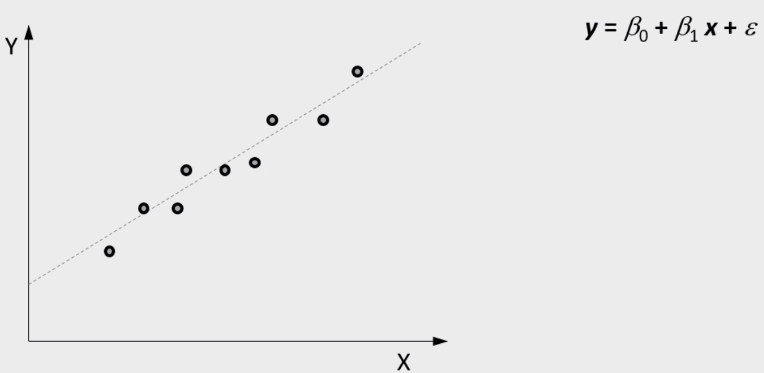
最小二乘法：
通过使因变量的真实值和估计值之间的离差平方和达到最小来求 β0 和 β1
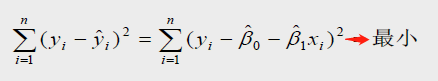
1.2 多元回归（今天先略过）
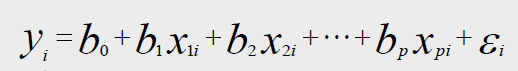
通过矩阵来求解最小二乘法
二、回归算法相关函数
使用 R 自带的 women 数据集
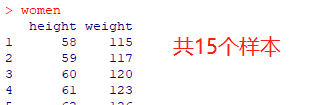
一元线性回归
# 模型创建 fit1 = lm(weight~.,data=women)
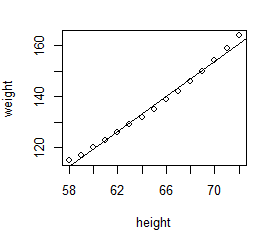
# 查看拟合结果 plot(women) abline(fit1)
发现点有些弯曲，可能存在二次关系
去除截距项的方法
# 除去截距项 fit2 = lm(weight~-1+height,data=women)
一元二次回归
# 模型创建 fit3 = lm(weight~.+I(height^2),data=women)
使用 summary 查看回归模型的信息
summary(fit3)
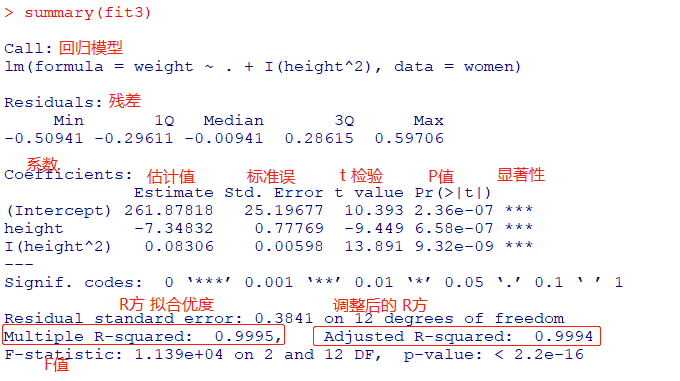
Tip：
R方：（决定系数、拟合优度）拟合出来的结果解释了多少数据点中的信息（代表拟合程度，越接近1越好）：可以用来评估模型拟合的好不好
F值：所有的参数是否为零（是否接受0假设），越小越拒绝0假设，检验模型整体指标的值
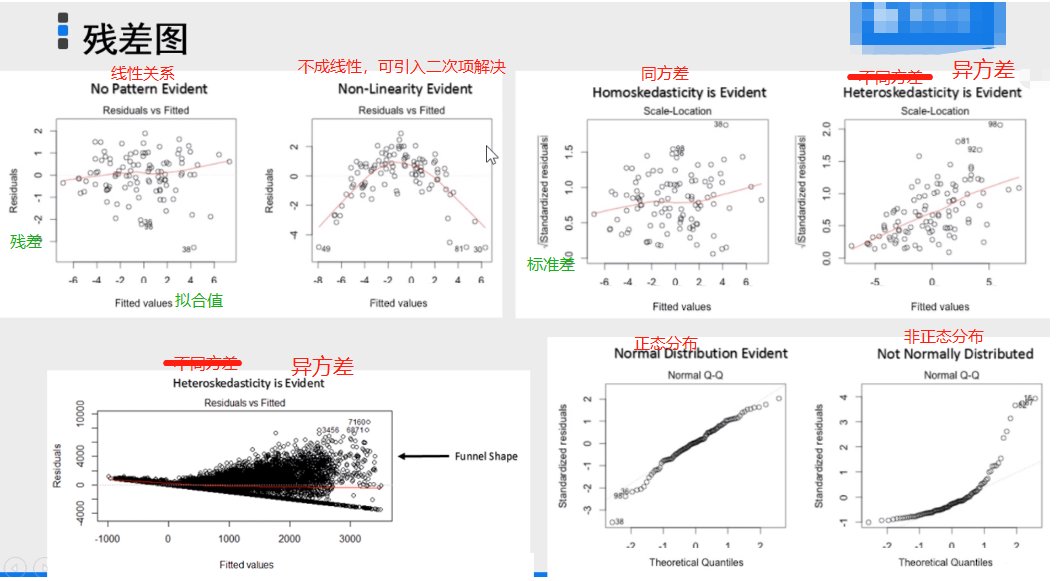
模型诊断
par(mfrow=c(2,2)) # par设置图片格式的函数（2*2的版式） plot(fit3)
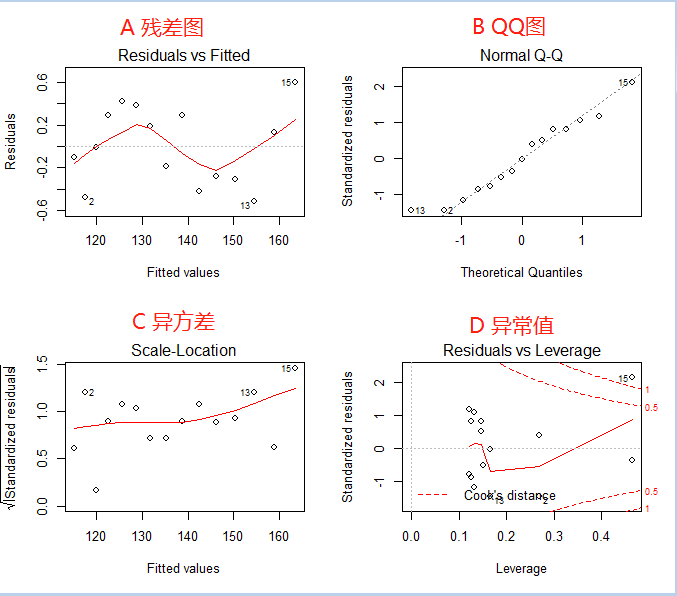
Tip：
A ：检查整体的拟合情况
B ：点越呈对角线分布，说明数据越呈正态分布
C ：曲线波动越明显，越可能异方差
D ：落在虚线外的点为异常值、离群值
回归的预测函数
lm.pred = predict(fit3, women)
如需预测区间：
interval ：给出相应的预测区间
level：置信水平
lm.pred = predict(fit3, women, interval="prediction", level=0.95) lm.pred
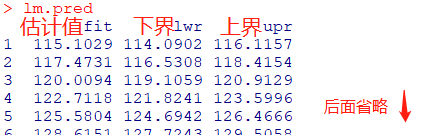
三、模型选择
指标：AIC信息准则即Akaike information criterion，又称赤池信息量准则。
AIC = 2k - 2ln(L)
方法：逐步回归（step）
AIC 可以权衡所估计模型的复杂度和此模型拟合数据的优良性。增加自由参数的数目提高拟合的优良性，为了尽量避免出现过度拟合(Overfitting)的情况。优先考虑AIC值最小的模型。
k：自变量的个数，
L 最大似然函数：越大，模型效果越好
# 导入数据集
state = read.csv("data_files/state.csv")
head(state)
# 设置行第一列为state的rownames
rownames(state) = state[,1]
# 删除第一列数据
state = state[,-1]
fit4 = lm(Murder~.,data= state)
par(mfrow=c(2,2))
plot(fit4)
summary(fit4)
# 通过pairs查看因变量和自变量的关系（散点图）
pairs(state)
fit5 = lm(Murder~.+ I(Income^2),data= state)
summary(fit5)
fit6 = lm(Murder~.+ I(Income^2)-Frost,data= state)
summary(fit6)
fit7 = lm(Murder~.+ I(Income^2)-Frost-Income,data= state)
summary(fit7)
fit8 = lm(Murder~.-Frost-Income,data= state)
summary(fit8)
fit9 = lm(Murder~.+ I(Income^2)+ I(Frost^2),data= state)
summary(fit9)
# 以默认的backword逐步回归（复杂到简单）
step(fit9)
也可以通过直接比较AIC的方法，找到AIC最小的模型
AIC(fit4,fit5,fit6,fit7,fit8,fit9)
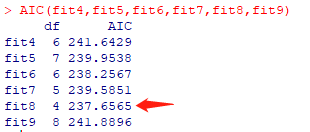
四、回归诊断
好的模型具备
无偏性：误差比较小
有效性：方差小
一致性：在大样本也会呈现同样的规律
不好的模型：
异方差
多重共线性
序列相关（自相关）
4.1 自相关性检验
DW检验：检验自相关性，
0 假设：自相关系数为0（不自相关）
备择假设：自相关系数比零大（自相关）
是不自相关，P值越大，越认为不相关
install.packages("car")
install.packages("lmtest")
library("car")
library("lmtest")
# dw 检验
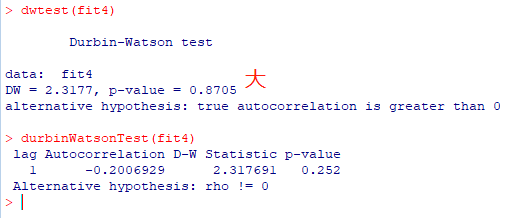
dwtest(fit4)
# 杜宾沃森检验
durbinWatsonTest(fit4)
P值很大，接收零假设，不存在自相关（而且DW值也很接近2）
4.1 异方差检验
零假设：同方差
备择假设：异方差
# 异方差 bptest(fit4) # 0 假设是同方差 ncvTest(fit4) # 0 假设是方差不变
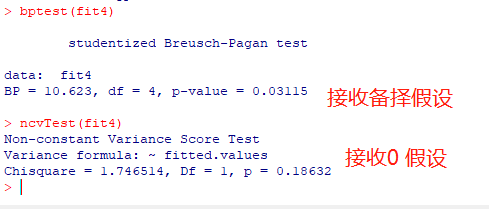
（该模型未通过同方差检验）
4.3 多重共线性
vif ：方差膨胀因子，0-10 说明不存在多重共线性
vif(fit4)
均不存在多重共线性的问题
如果存在多重共线性，解决方法可以参考 简化模型
即去掉存在共线的自变量（具体根据业务）
仅用于学习
