聚类分析 | 概述、 k均值聚类算法 KMeans 处理数据及可视化

一 概述

• 聚类分析目的
  • 将大量数据集中具有“相似”特征的数据点或样本划分为一个类别
• 常见应用场景
  • 在没有做先验经验的背景下做的探索性分析
  • 样本量较大情况下的数据预处理工作
  • 将数值类的特征分成几个类别
• 聚类分析能解决的问题包括
  • 数据集可以分为几类
  • 每个类别有多少样本量
  • 不同类别中各个变量的强弱关系如何
  • 不同类别的典型特征是什么
• k均值聚类算法 KMeans
• 注意事项
  • 需要处理异常值
  • 如果建模的特征中，量纲差距比较大，需要做归一化/标准化
• 创建KMeans对象 建模
• n_cluster 聚类个数
• init='k-means++' 在选点的时候，找距离初始点比较远的点
• random_state  随机种子数
• kmeans.inertia_ 簇内误差平方和
• 轮廓系数 metrics.silhouette_score()
• kmeans_model.cluster_centers_ 聚类中心点
• kmeans_model.labels_ 聚类之后的标签

二 案例

1 数据准备

import pandas as pd
df = pd.read_csv('data.csv')

# 使用最后两列作为分群依据
x = df.iloc[:,3:].values

 

 2 创建 KMeans 模型，进行聚类【核心代码】

# 导包
from sklearn.cluster import KMeans

# 模型创建
kmeans_model = KMeans(n_clusters=5, init='k-means++', random_state= 11)

# 进行聚类处理
y_kmeans = kmeans_model.fit_predict(x)

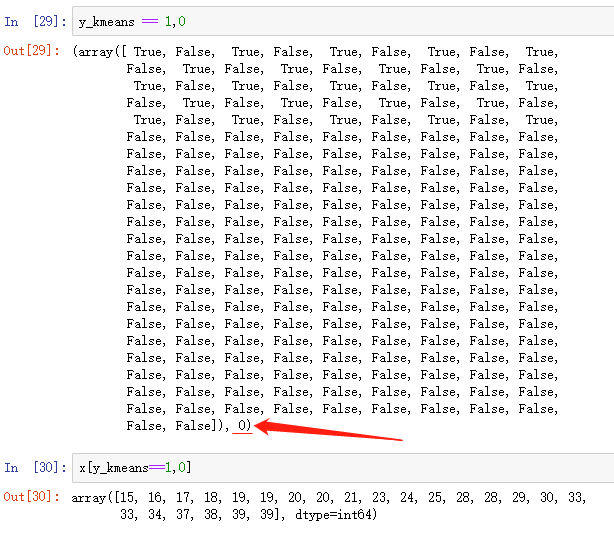
 此时已经将数据 分成了5类，将标签加入数据中

 

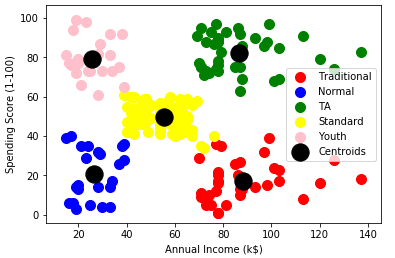
 3 聚类结果可视化

# 导入可视化工具包
import matplotlib.pyplot as plt
%matplotlib inline

# 颜色和标签列表
colors_list = ['red', 'blue', 'green','yellow','pink']
labels_list = ['Traditional','Normal','TA','Standard','Youth']

# 需要将DataFrame转成ndarray,才能进行 x[y_kmeans==i,0]
x = x.values

for i in range(5):
    plt.scatter(x[y_kmeans==i,0], x[y_kmeans== i,1], s=100,c=colors_list[i],label=labels_list[i])

# 聚类中心点
plt.scatter(kmeans_model.cluster_centers_[:,0],kmeans_model.cluster_centers_[:,1], s=300,c='black',label='Centroids')

plt.legend()
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.show()

 

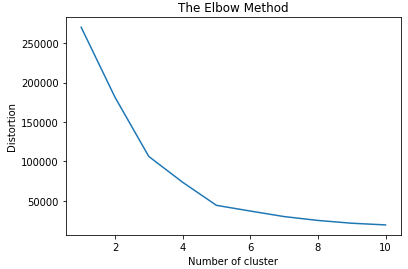
4 评估聚类个数

# 用于盛放簇内误差平方和的列表
distortion = []

for i in range(1,11):
    kmeans = KMeans(n_clusters=i,init='k-means++', random_state=11)
    kmeans.fit(x)
    distortion.append(kmeans.inertia_)
    
plt.plot(range(1,11), distortion)

plt.title('The Elbow Method')
plt.xlabel('Number of cluster')
plt.ylabel('Distortion')
plt.show()

 

完成辣！

附几个变量说明，便于复习

 

========================

 

 

========================

 

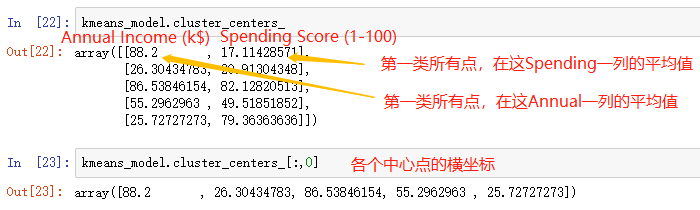
 本文仅用于学习