浅谈多种方法求LCA(最近公共祖先)
LCA
首先来看下例题
洛谷 P3379 点这里看题目
相信求LCA是每位Oier学习算法的必经之路
那么啥是LCA呢?
引用OI wiki的定义——

那么步入正题 如何求LCA呢?
第一种方法·朴素求法
我们选择深度最深的点往上跳 最后两点一定会相遇 相遇的位置即是我们要的LCA
dfs整棵树是O(n)的,单次查询复杂度为O(n),但实际是log(n)的(随机树高)
第二种方法·倍增求LCA
首先 啥是倍增呢?(应该没有人不知道) 如果不知道的话请看这

参考代码:
#include<bits/stdc++.h> using namespace std; const int maxn=500010; int dep[maxn],head[maxn],n,m,s,cnt=0,fa[maxn][23]; int Log[maxn]; inline int read() { char ch; int res,sign=1; while((ch=getchar())<'0'||ch>'9') if(ch=='-') sign=-1; res=ch^48; while((ch=getchar())>='0'&&ch<='9') res=(res<<1)+(res<<3)+(ch^48); return res*sign; } struct edge{ int next,to; }e[maxn<<1]; inline void add(int u,int v) { e[++cnt].to=v; e[cnt].next=head[u]; head[u]=cnt; } inline void dfs(int now,int father) { fa[now][0]=father; dep[now]=dep[father]+1; for(register int i=1;i<=Log[dep[now]];++i) { fa[now][i]=fa[fa[now][i-1]][i-1]; } for(int i=head[now];i;i=e[i].next) { int v=e[i].to; if(v!=father) { dfs(v,now); } } } inline int lca(int x,int y) { if(dep[x]<dep[y]) swap(x,y); while(dep[x]>dep[y]) { x=fa[x][Log[dep[x]-dep[y]]-1]; } if(x==y) return x; for(register int k=Log[dep[x]];k>=0;k--) { if(fa[x][k]!=fa[y][k]) { x=fa[x][k]; y=fa[y][k]; } } return fa[x][0]; } int main() { n=read(),m=read(),s=read(); for(register int i=1;i<=n-1;++i) { int x,y; x=read(),y=read(); add(x,y); add(y,x); } for(register int i=1;i<=n;++i) { Log[i]=Log[i-1]+(1<<Log[i-1]==i); } dfs(s,0); for(register int i=1;i<=m;++i) { int x,y; x=read(),y=read(); printf("%d\n",lca(x,y)); } return 0; }
第三种方法·Tarjan
待更新
第四种方法·树链剖分
由树链剖分的性质可知
我们每次求LCA(x,y)的时候可以先判断两点是否在同一链上
如果两点在同一条链上我们只要找到这两点中深度较小的点输出就行了
如果两点不在同一条链上
那就找到深度较大的点令它等于它所在的重链链端的父节点即为x=fa[top[x]]
直到两点到达同一条链上,输出两点中深度较小的点
inline int lca(int u, int v) { while (top[u] != top[v]) { if (dep[top[u]] > dep[top[v]]) u = fa[top[u]]; else v = fa[top[v]]; } return dep[u] > dep[v] ? v : u; }
程序code:
#include<cstdio> #include<iostream> #define ri register using namespace std; int nxt[1000005],to[1000005]; int n,m,s,ecnt=0,head[500005],dep[500005],siz[500005],son[500005],top[500005],fa[500005]; void add(int x,int y) { to[++ecnt]=y; nxt[ecnt]=head[x]; head[x]=ecnt; } inline int read() { char ch; int res,sign=1; while((ch=getchar())<'0'||ch>'9') if(ch=='-') sign=-1; res=ch^48; while((ch=getchar())>='0'&&ch<='9') res=(res<<1)+(res<<3)+(ch^48); return sign*res; } inline void dfs1(int p) { siz[p]=1; dep[p]=dep[fa[p]]+1; for(register int i=head[p];i;i=nxt[i]) { int dd=to[i]; if(dd==fa[p])continue; fa[dd]=p; dfs1(dd); siz[p]+=siz[dd]; if(!son[p]||siz[son[p]]<siz[dd]) son[p]=dd; } } void dfs2(int x,int tv) { top[x]=tv; if(son[x])dfs2(son[x],tv); for(ri int i=head[x];i;i=nxt[i]) { int dd=to[i]; if(dd==fa[x]||dd==son[x])continue; dfs2(dd,dd); } } inline void init(int root) { dfs1(root),dfs2(root,root); } inline int lca(int u, int v) { while (top[u] != top[v]) { if (dep[top[u]] > dep[top[v]]) u = fa[top[u]]; else v = fa[top[v]]; } return dep[u] > dep[v] ? v : u; } int main() { n=read(),m=read(),s=read(); for(ri int i=1;i<n;++i) { int x,y; x=read(),y=read(); add(x,y); add(y,x); } init(s); for(ri int i=1;i<=m;++i) { int x,y; x=read(),y=read(); printf("%d\n",lca(x,y)); } }
第五种方法·RMQ求LCA
重点讲一下RMQ!
其实很简单啦 我们可以先通过dfs求出长度为2n-1的欧拉序列
用一个fir数组记录每个i第一次出现的位置
有了欧拉序列 我们就可以在线性时间内把求LCA转换成RMQ问题,也就是
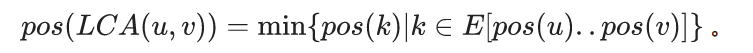
这个式子很好理解,由于dfs我们可以知道对于两点u和v从u走到v一定会经过LCA并且不会经过lca(u,v)的祖先,所以从u走到v深度最小的节点必然是lca(u,v),所以我们可以用ST表来处理出各区间之间深度的RMQ,对于每个询问O(1)就能输出答案,并且预处理也只用O(nlogn)
参考代码:
#include<bits/stdc++.h> using namespace std; int n,m,s,cnt=0,tot=0; const int maxn=1000010; int head[maxn],f[maxn][25],Log[maxn],rec[maxn][25]; int fir[maxn],ver[maxn],r[maxn];//fir[i] is the first position of i //ver[i]欧拉序;r[i]是ver[i]所处深度 struct edge { int next,to; }e[maxn<<1]; inline void add(int x,int y) { e[++cnt].to=y; e[cnt].next=head[x]; head[x]=cnt; } inline int read() { char ch; int res,sign=1; while((ch=getchar())<'0'||ch>'9') if(ch=='-') sign=-1; res=ch^48; while((ch=getchar())>='0'&&ch<='9') res=(res<<1)+(res<<3)+(ch^48); return res*sign; } inline void dfs(int u,int dep) { fir[u]=++tot,ver[tot]=u,r[tot]=dep; for(int i=head[u];i!=-1;i=e[i].next) { int v=e[i].to; if(!fir[v]) { dfs(v,dep+1); ver[++tot]=u,r[tot]=dep; } } }int main() { memset(head,-1,sizeof(head)); n=read(),m=read(),s=read(); for(int i=1;i<n;i++) { int x,y; x=read(),y=read(); add(x,y); add(y,x); } dfs(s,1); //pre(); for(register int i=1;i<=tot;++i) { f[i][0]=r[i],rec[i][0]=ver[i]; } for(register int j=1;j<=log(tot)/log(2);++j) for(register int i=1;i+(1<<j)-1<=tot;++i) { if(f[i][j-1]<f[i+(1<<(j-1))][j-1]) { f[i][j]=f[i][j-1],rec[i][j]=rec[i][j-1]; } else { f[i][j]=f[i+(1<<(j-1))][j-1],rec[i][j]=rec[i+(1<<(j-1))][j-1]; } } for(int i=1;i<=m;i++) { int l,r; l=read(),r=read(); l=fir[l],r=fir[r]; if(l>r) swap(l,r); int k=0; while((1<<k)<=r-l+1) k++; k--; if(f[l][k]<f[r-(1<<k)+1][k]) printf("%d\n",rec[l][k]); else printf("%d\n",rec[r-(1<<k)+1][k]); } return 0; }}
理论上是这样 然而事实是:
树剖做法

RMQ做法

倍增法

惊了!!!
以上就是全部内容!!!后续会更新一些题目和算法~

