【软工】结对项目作业
| 项目 | 内容 |
|---|---|
| 作业所属的课程 | 2020春季计算机学院软件工程(罗杰 任健) |
| 作业的要求 | 结对项目作业 |
| 我在这门课程的目标是 | 学会使用软件工程的设计思想和方法,能够设计出高效并且可用性、可维护性、可拓展性较高的软件。 |
| 这个作业在哪些方面帮助我实现目标 | 体验结对编程,学习结对同学的设计思路与编码习惯,学会交流与适应。 |
| 参考资料 | 《构建之法:现代软件工程(邹欣 著)》等。 |
| 教学班级 | 005 |
| 项目地址 | https://github.com/CookieLau/intersection.git |
PSP表格记录
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| · Estimate | · 估计这个任务需要多少时间 | 40 | 40 |
| Development | 开发 | ||
| · Analysis | · 需求分析 (包括学习新技术) | 300 | 360 |
| · Design Spec | · 生成设计文档 | 100 | 100 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 60 | 60 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 30 |
| · Design | · 具体设计 | 180 | 200 |
| · Coding | · 具体编码 | 300 | 320 |
| · Code Review | · 代码复审 | 180 | 180 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 180 | 180 |
| Reporting | 报告 | ||
| · Test Report | · 测试报告 | 100 | 80 |
| · Size Measurement | · 计算工作量 | 30 | 20 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 20 | 10 |
| 合计 | 1620 | 1680 |
这次除了编码之外,在进行需求分析学习新技术的时候也花费了很多时间,特别是因为之前没有GUI的编程经验,在考虑使用的方法和模块是在查找上花费了很多时间。同时由于是结对编程,在代码复审上也花费了不少的时间,我的合结对伙伴在构思和编码能力上都要比我强好多,所以最开始进行扩展基本是基于结对伙伴的代码,对于其中一些设计思想的理解花费了一些时间。
Information Hiding、Interface Design与Loose Coupling
Information hiding is part of the foundation of both structured design and object-oriented design. In structured design, the notion of “black boxes” comes from information hiding. In object-oriented design, it gives rise to the concepts of encapsulation and modularity, and it is associated with the concept of abstraction.
选自Code Complete Section 5.3
所谓Information Hiding即在不同的功能模块进行封装,并提供其他模块调用时使用的接口,使得其他模块在调用时能够屏蔽掉其内部实现的细节,同时也能够限制调用者对于被调用者内部的修改,提高其安全性。我们对程序的core部分进行了封装,使各种图形Shape类对调用者不可见。这样避免了调用者对于Shape类的直接操作,将其能够进行的操作进行了限制,保证了内部核心的实现的安全性。
同时,对于核心模块对外的接口,即Interaction类,该类提供了一系列方法供调用者使用,例如读取文件中的点,求解交点个数等函数。命令行的main函数以及GUI都通过调用此接口完成一系列功能。
对于Loose Coupling松解耦,指的是尽可能使不同模块之间的调用通过各个模块提供的接口实现,而避免一个模块对于另一个模块内部其他功能的依赖,这样在进行扩展或重构时,能够防止因模块之间的耦合而造成的修改的困难与相互影响。在我们的项目中,通过使用Interaction类提供接口,同时向下屏蔽图形类中的具体实现细节,来实现减少命令行的主函数以及GUI对于核心模块的耦合。
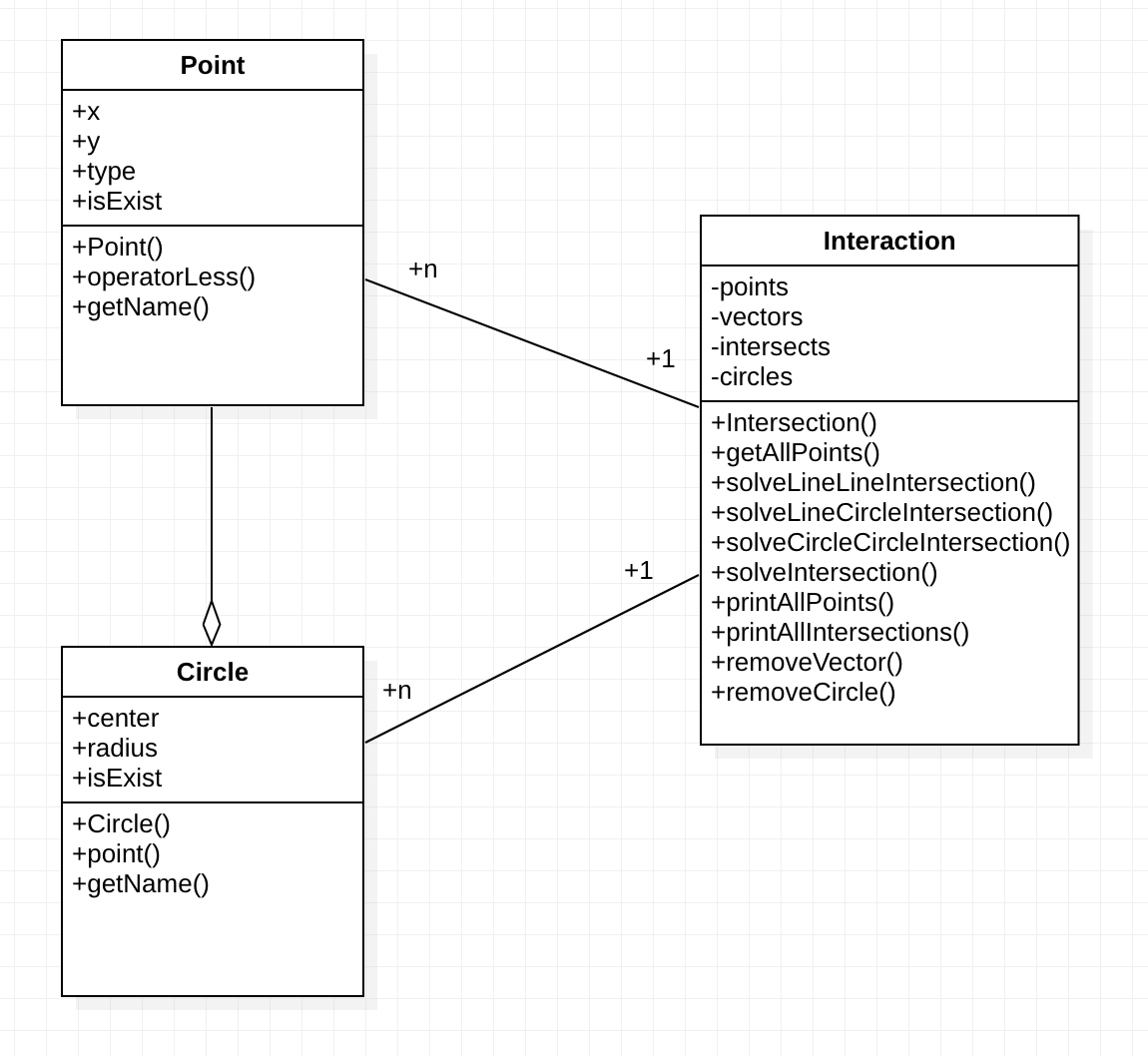
计算模块接口的设计与实现过程
计算模块主要包括三个类,分别是两个图形类(向量类、圆类)以及一个Interaction类,将其用作计算模块向外的接口,提供读入数据以及求解的方法。整体关系上,在Interaction类中通过读入文件创建向量类和圆类的对象实例,同时在求解时调用其相关的方法。
-
Shape
- Point(Vector)
- 构造方法
- 重写运算符:< + - * / ==
- 求解向量长度:double Length(Vector A)
- 求解内积:double Dot(Vector A, Vector B)
- 求解外积:double Cross(Vector A, Vector B)
- 求向量夹角:double Angle(Vector A, Vector B)
- 其他相关函数
- Circle
- 构造方法
- 求解圆上一点坐标:Point Circle::point(double angle)
- 其他用于在求解交点时计算相关边长的函数
- Point(Vector)
-
Interaction
-
读取文件:int Intersection::getAllPoints(ifstream& in)
- 对于线,保存第一个点的坐标,由第一个点指向第二个点的向量,以及其类型(线段、射线、直线)
- 对于圆,保存圆心坐标以及半径长度
-
求解两条线的交点:void Intersection::solveLineLineIntersection()
-
求解线和圆的交点:void Intersection::solveLineCircleIntersection()
-
求解圆和圆的交点:void Intersection::solveCircleCircleIntersection()
-
上述三个方法整体的思路与之前个人项目中的思路相似,不同在于这次增加了射线和线段,因此在求解线和线、线和圆,求解出交点后,要判断其是否同时在两个图形上。根据上文我们对于图形保存方式的介绍,设计算出的一个点为M,确定一条线段、射线、直线的第一个点为P,第二个点为Q,记t=PM·P q/PQ·PQ,这样,对于直线,此交点一定在直线上,对于射线,需要t>=0,对于线段,需要0<=t<=1。通过这种方式,不需要对之前的代码进行太多的修改,只要对求解出的可能的交点进行一下合法性的判断即可。做到了在很大程度上复用之前的代码。
bool LineIsValid(char type, double t) { switch (type) { case 'L': return true; case 'R': return dcmp(t) >= 0; case 'S': return dcmp(t - 1.0) <= 0 && dcmp(t) >= 0; default: return false; } }
-
UML图
计算模块接口部分的性能改进
这次开始进行结对时基于的是对方同学的代码,首先,在之前个人项目中,我使用的是set对求出的交点进行去重,但是在进行性能分析是如下图所示,主要花费的时间在于对set进行insert操作。因为在使用set时内部维护了一个红黑树,而每次进行插入时都会花费时间对其进行维护,因此这样效率比较低。
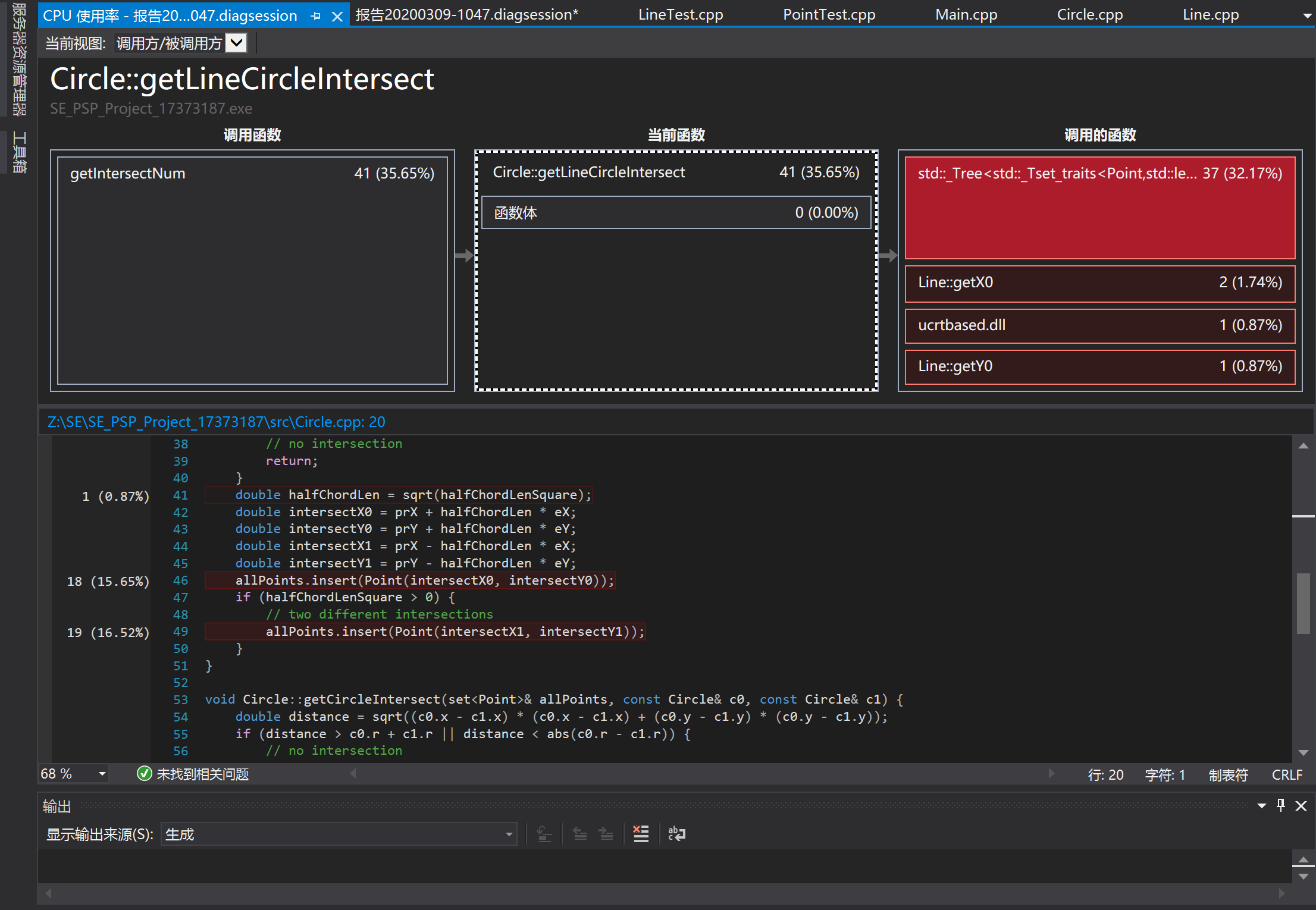
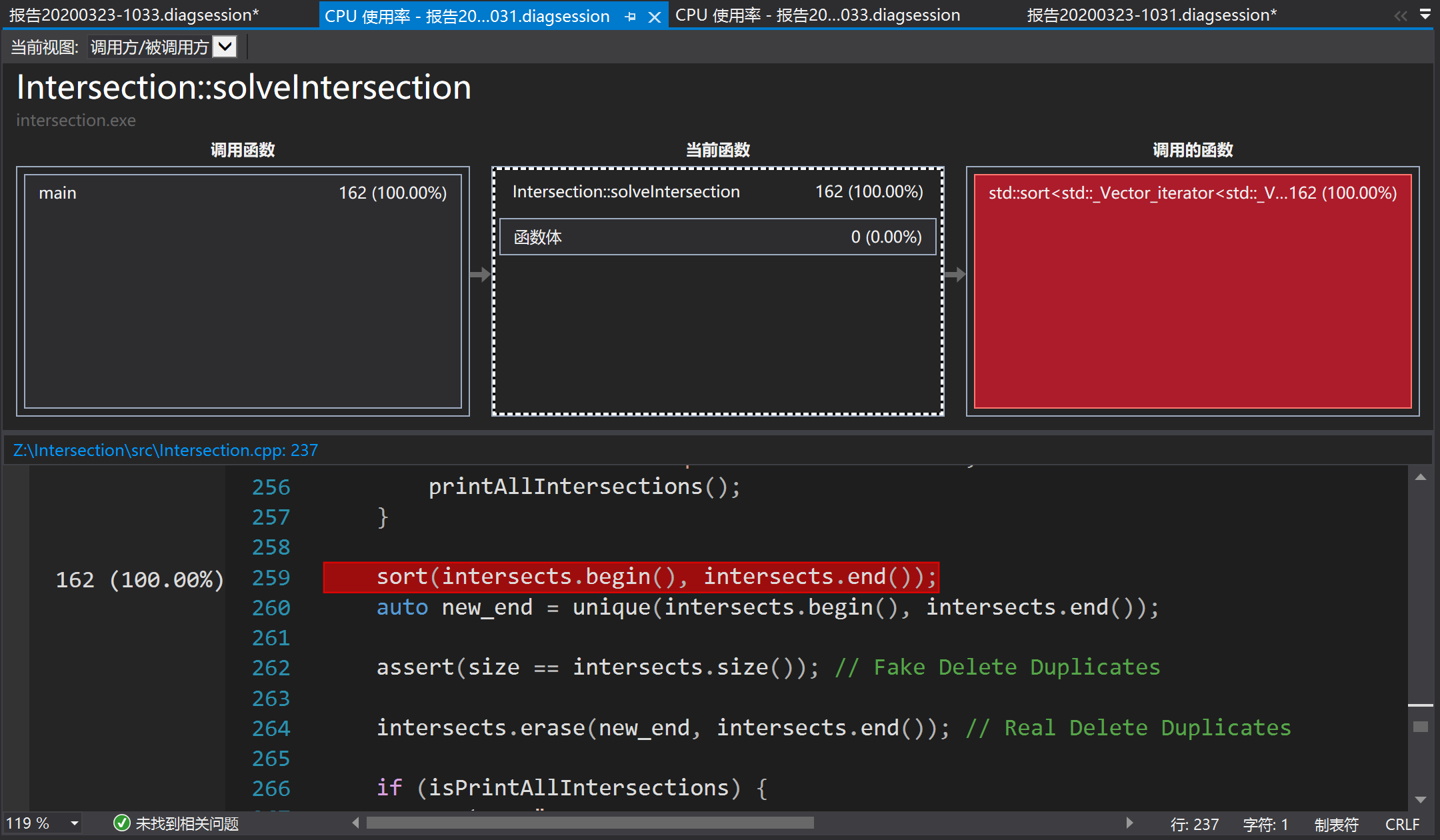
在结对同学的代码中使用的是vector,在插入时时间的消耗是非常小的,同时只要在最后进行去重,花费的时间每次都要对红黑树进行维护的时间要少很多。即:
sort(intersects.begin(), intersects.end());
auto new_end = unique(intersects.begin(), intersects.end());
intersects.erase(new_end, intersects.end()); // Real Delete Duplicates
这样,在使用同样的大小进行测试时,在原来的程序中对于长度为40000的数据而言,执行时间超过了一分钟,而在使用vector,最后进行去重,使用的时间约为37秒。如下图所示:

这一次对于时间消耗最大的方法在用上述的sort操作,而对于vector的push_back操作所占的时间则很少。
计算模块部分单元测试展示
我们针对计算部分,分别准备了10余个综合测试用例,并且每一个方法都准备了相应的单元测试用例。
计算模块部分异常处理说明
异常处理分为两部分,分别是对于读取输入时的异常处理以及在对图形进行处理时的异常处理。
-
输入时的异常包括
-
出现值错误,无法读入:包括出现非法字符等
-
构成线段、射线或直线的两点重合
-
出现超范围的数据
-
圆的半径应大于0
-
-
处理过程中的异常主要包括直线、射线和线段之前有重合导致出现了无数多交点的情况。具体判别方法和代码如下。在共线情况下:
-
只要出现直线,就一定会出现无穷多交点的情况
-
如果是两个射线,先对其方向向量进行点乘
- 若为正,则必有无穷多交点
- 否则,根据射线起点组成的向量与射线方向向量的内积进行确定,具体见下方代码中注释
// 对方向向量进行点乘,如果同向则error double judge = Dot(vectors[i], vectors[j]); if (dcmp(judge) > 0) { throw string("射线与射线重合"); } // 不同向,用射线起点组成的向量与其中一个方向向量点乘 Point ppv = points[j] - points[i]; // 从i指向j judge = Dot(ppv, vectors[i]); // ppv 与i的方向向量内积 if (dcmp(judge) > 0) { throw string("射线与射线重合"); } else if (dcmp(judge) == 0) { // 有一个交点,即射线起点 intersects.push_back(points[i]); } else { continue; } -
如果是射线和直线的情况,那么需要根据由射线的起点与线段的两个端点构成的向量进行判断,请见下方代码。其中,我们使用一个点point和其方向向量vector表示线。
Point rsv0 = points[j] - points[i]; Point rsv1 = vectors[j] + points[j] - points[i]; double judge0 = Dot(vectors[i], rsv0); double judge1 = Dot(vectors[i], rsv1); if (dcmp(judge0) < 0 && dcmp(judge1) < 0) { continue; } else if ((dcmp(judge0) < 0 && dcmp(judge1) == 0) || (dcmp(judge0) == 0 && dcmp(judge1) < 0)) { // 此时有唯一焦点为射线起点 intersects.push_back(points[i]); } else { throw string("射线与线段重合"); } -
如果是两个线段,因为我们是在已知共线的条件下进行判定的,因此利用这一条件,我们可以使用其在x轴上的投影点的坐标进行判定(如果平行于y轴,则使用在y轴的投影点的坐标)。
Point iSmall = (dcmp(vectors[i].x) > 0) ? points[i] : (points[i] + vectors[i]); Point iLarge = (dcmp(vectors[i].x) > 0) ? (points[i] + vectors[i]) : points[i]; Point jSmall = (dcmp(vectors[j].x) > 0) ? points[j] : (points[j] + vectors[j]); Point jLarge = (dcmp(vectors[j].x) > 0) ? (points[j] + vectors[j]) : points[j]; if (dcmp(vectors[i].x) == 0) { // 与y轴平行,用纵坐标 // ... } else { // 用横坐标 if (iSmall.x > jLarge.x || jSmall.x > iLarge.x) { continue; } else if (iSmall.x == jLarge.x || jSmall.x == iLarge.x) { // 一个的小等于另一个的大,有一个重合的点 if (iSmall.x == jLarge.x) { intersects.push_back(iSmall); } else { intersects.push_back(jSmall); } } else { throw string("线段与线段重合"); } }
-
在对错误处理进行单元测试时,基本通过在文件中写用例,然后加载文件,判断其是否抛出了指定的错误。对于以上介绍的错误,每一项举一个例子:
TEST_METHOD(INPUT_0)
{
try {
ifstream in("../test/errortestcase/0.txt");
Intersection* intersect = new Intersection();
intersect->getAllPoints(in);
Assert::IsTrue(false);
}
catch (string msg) {
Assert::AreEqual(string("在第2行,出现未识别符号"), msg);
}
}
2
L 1 1 1 0
P 1 2 3 4
TEST_METHOD(LL_0)
{
try {
ifstream in("../test/errortestcase/5.txt");
Intersection* intersect = new Intersection();
intersect->getAllPoints(in);
intersect->solveIntersection();
Assert::IsTrue(false);
}
catch (string msg) {
Assert::AreEqual(string("直线与直线或线段重合"), msg);
}
}
2
L 1 1 2 2
L -1 -1 0 0
TEST_METHOD(LR_0)
{
try {
ifstream in("../test/errortestcase/6.txt");
Intersection* intersect = new Intersection();
intersect->getAllPoints(in);
intersect->solveIntersection();
Assert::IsTrue(false);
}
catch (string msg) {
Assert::AreEqual(string("直线与直线或线段重合"), msg);
}
}
2
L 1 1 2 2
R -1 -1 0 0
TEST_METHOD(RR_0)
{
try {
ifstream in("../test/errortestcase/7.txt");
Intersection* intersect = new Intersection();
intersect->getAllPoints(in);
int ret = intersect->solveIntersection();
Assert::AreEqual(ret, 0);
}
catch (string msg) {
Assert::IsTrue(false);
Assert::AreEqual(string("直线与直线或线段重合"), msg);
}
}
2
R 1 1 2 2
R 0 0 -1 -1
我们针对错误处理的每种情况,一共准备了约20个用例进行测试。
界面模块的详细设计过程
-
UI
- 图形绘制与展示,使用QWidget,使用QPainter在其上进行绘图。
- 一些按钮,例如打开文件,求解等,使用PushButton,将其clicked()信号与相关槽函数进行绑定。
- 显示导入的所有图形和坐标,使用ListWidget。
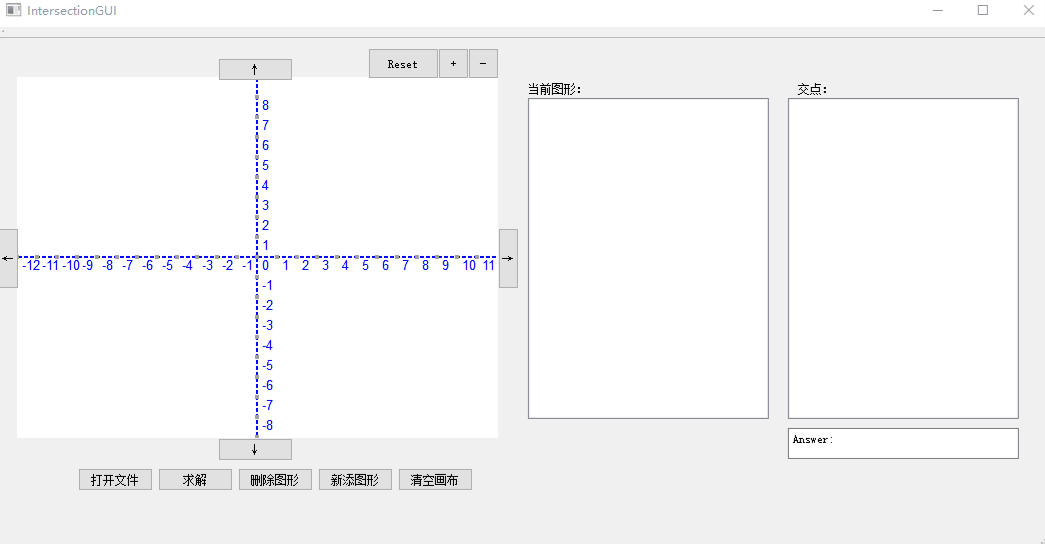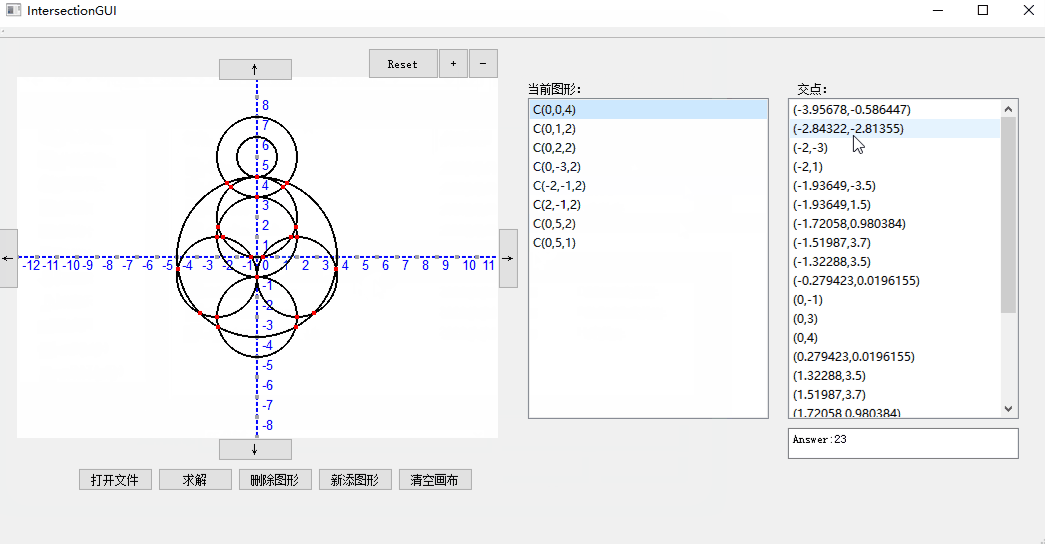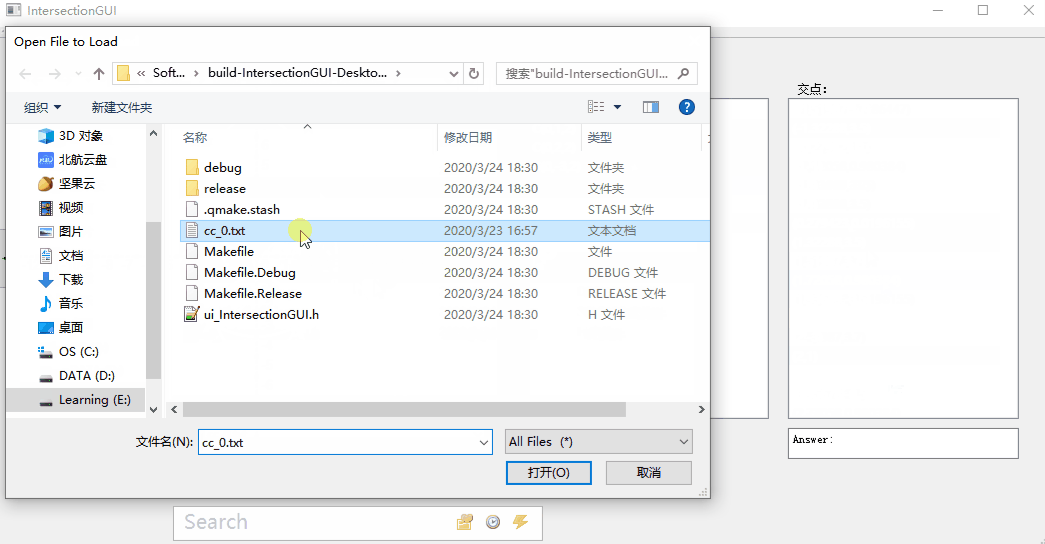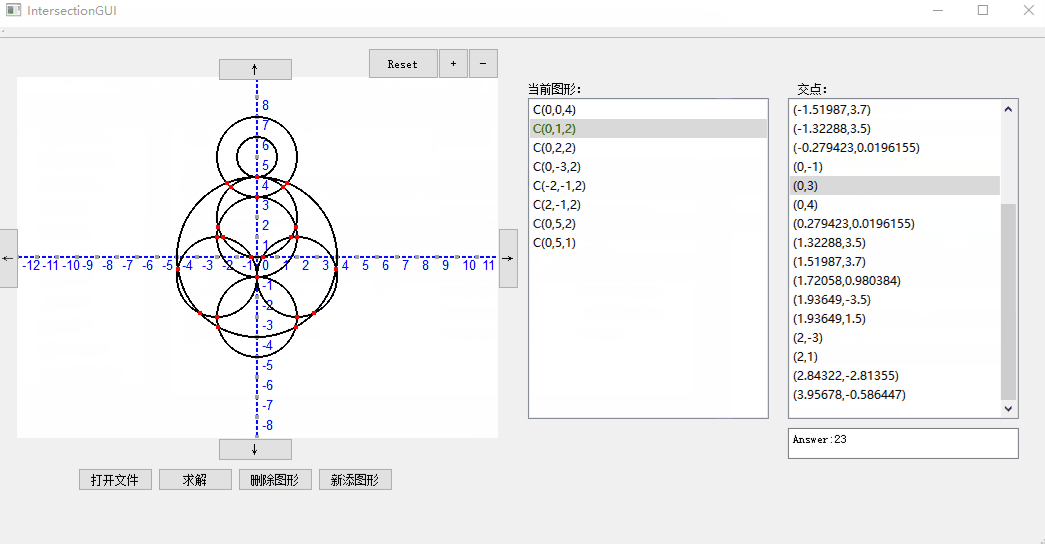
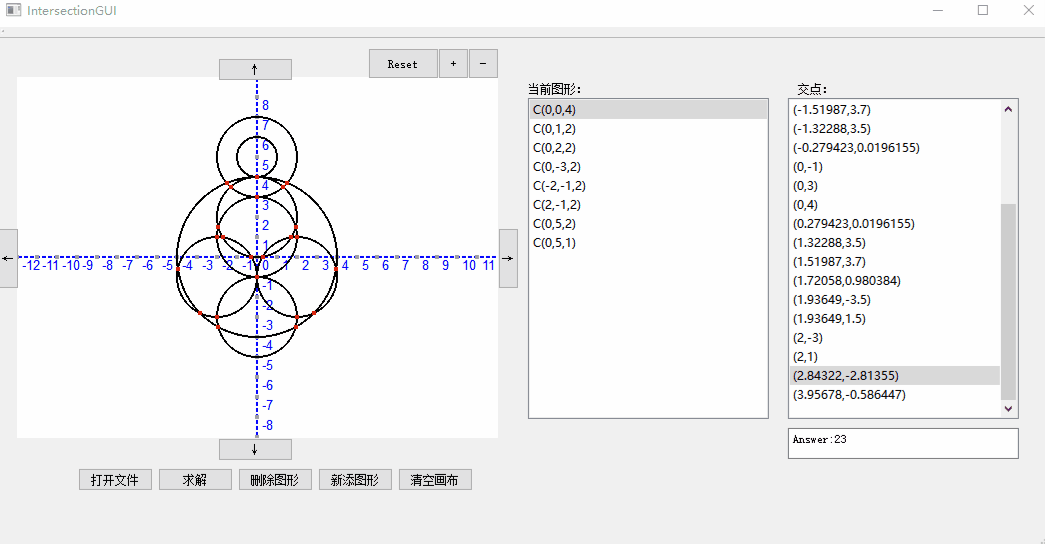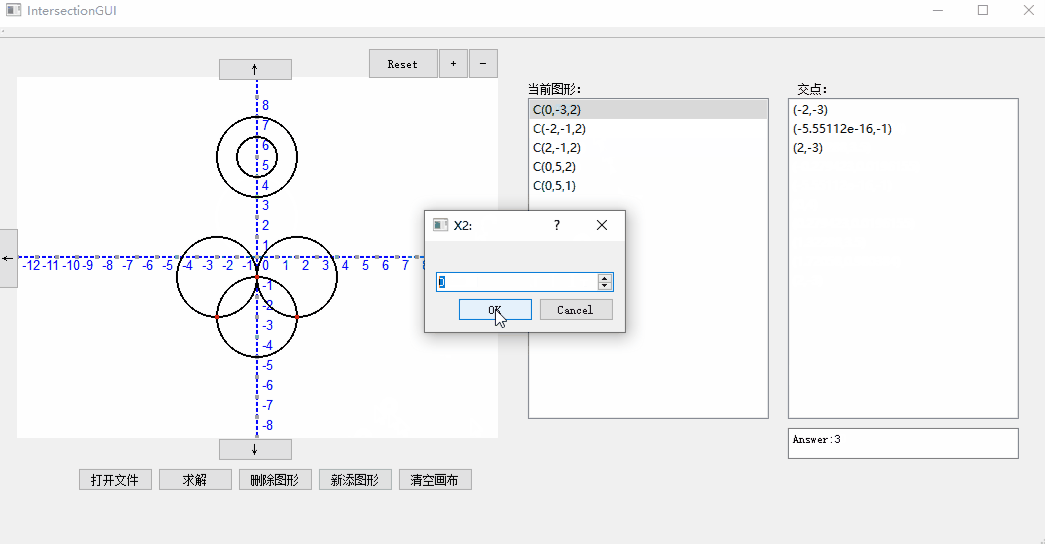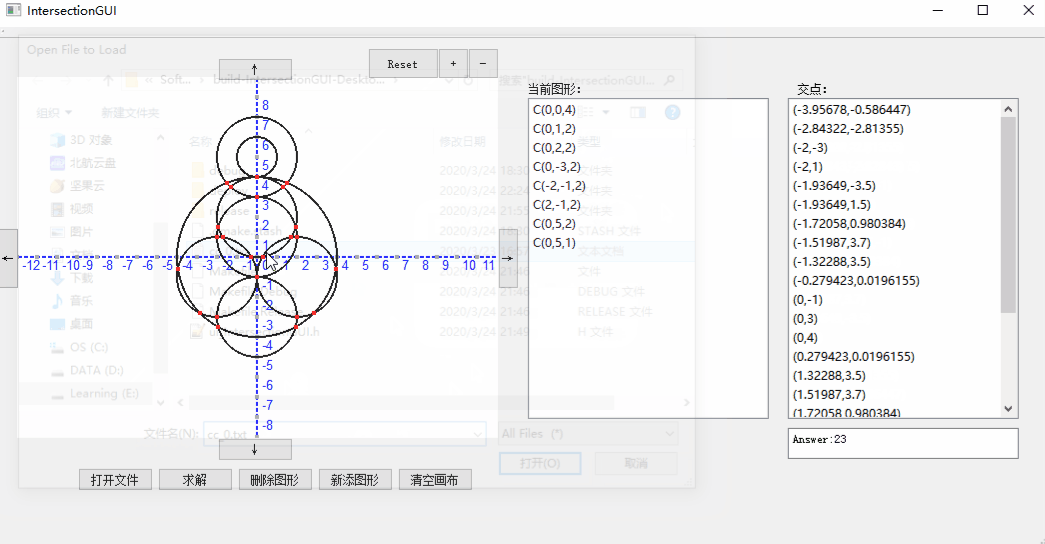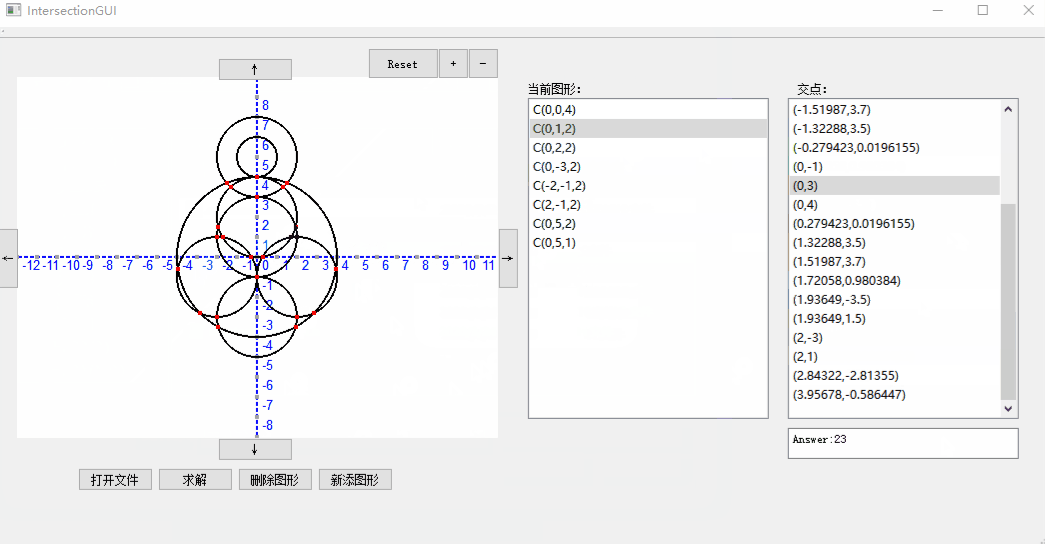
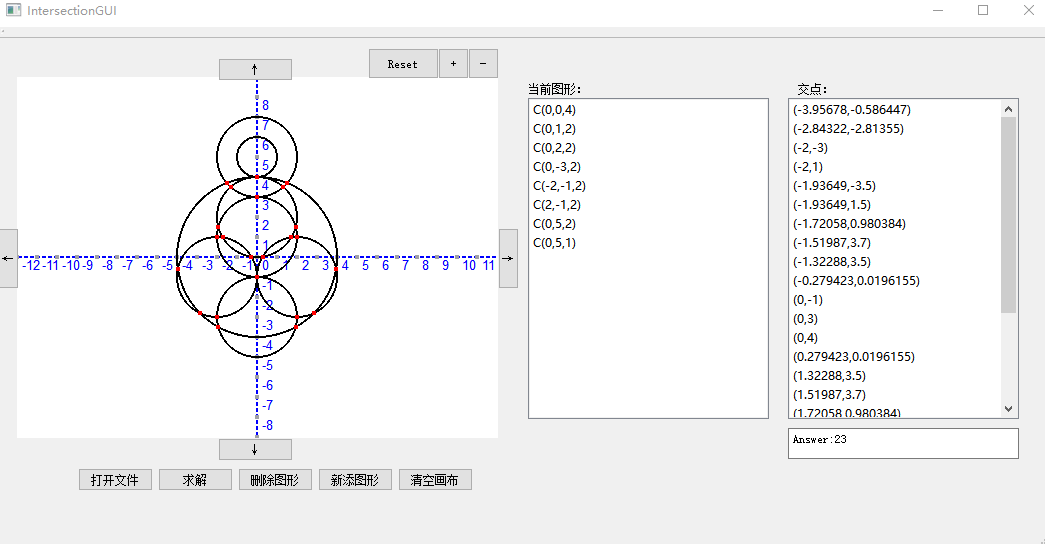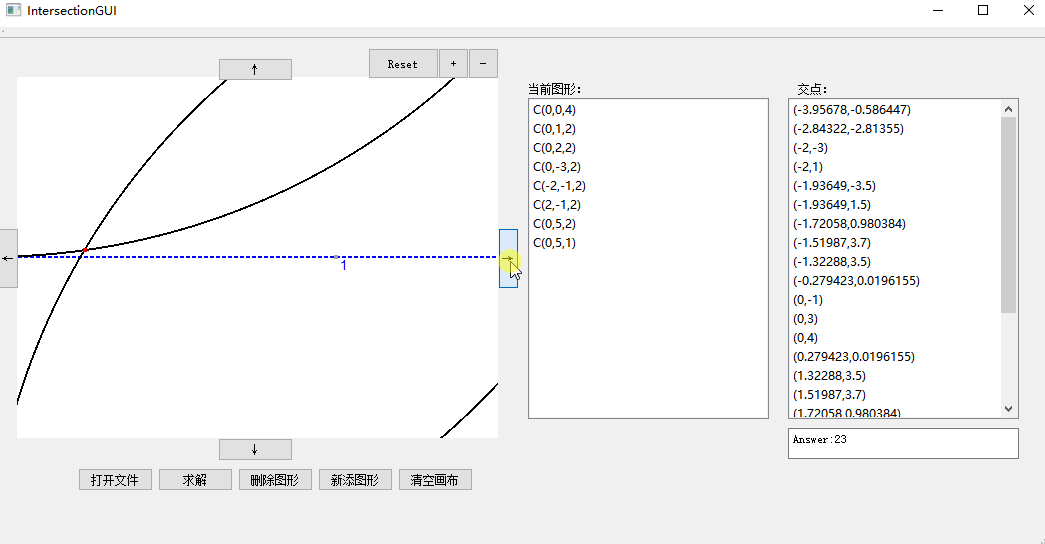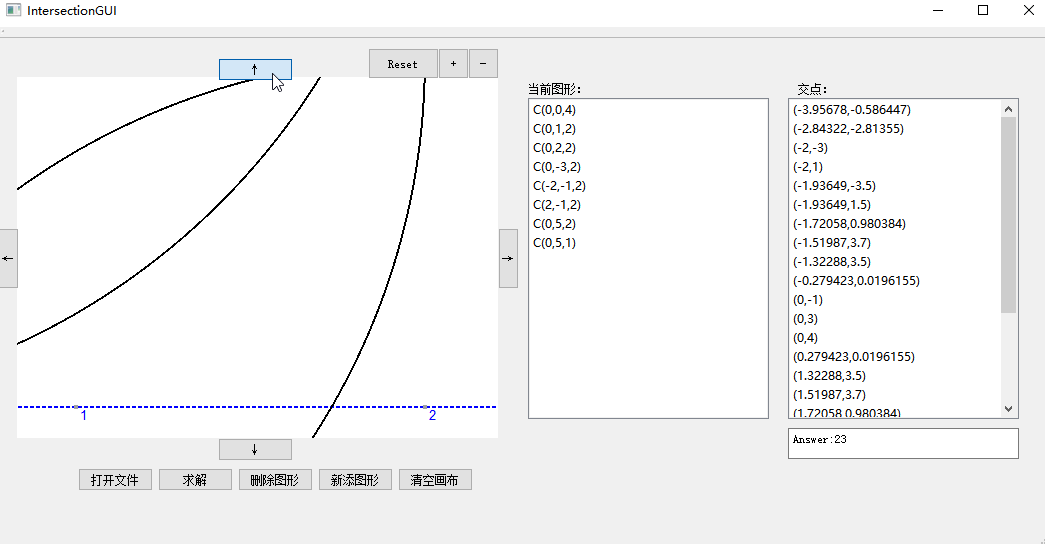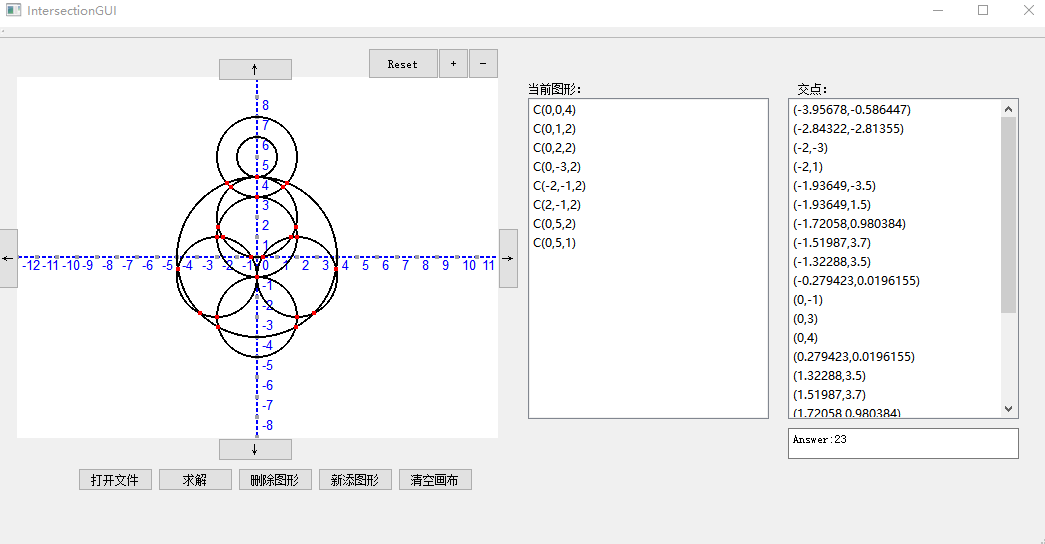
- 界面如下所示:
![]()
-
相关的函数
关于打开文件、求解等函数,由于设计到与core进行交互的内容,所以放到下一小节进行介绍,这里主要介绍一下与绘图相关的函数。在绘图中最主要的是paintEvent()函数。主要思路就是针对每一种图形进行遍历来绘制,具体细节请见代码注释。
void ShowPic::paintEvent(QPaintEvent *event) { QPainter painter(this); //painter.setPen(Qt::blue); QPen pp; pp.setWidth(2); pp.setColor(Qt::blue); pp.setStyle(Qt::DotLine); painter.setPen(pp); QLineF axis_X(0, y_offset, x_offset*2, y_offset); QLineF axis_Y(x_offset, 0, x_offset, y_offset*2); painter.drawLine(axis_X); painter.drawLine(axis_Y); pp.setColor(Qt::black); pp.setStyle(Qt::SolidLine); painter.setPen(pp); // 因为是左上角为基准点,所以要加上偏移量 double multipleSize = 1e9; double x1, y1; // x1, y1 point double v1, v2; double radius; QLineF line; QRectF circle; // 画基本图形 int type; // 遍历基本图形 if (intersection == nullptr) { return; } std::vector<Point> linePoints = intersection->getPoints(); std::vector<Vector> vectors = intersection->getVectors(); for (int i = 0; i < linePoints.size(); ++i) { if (!linePoints[i].isExist) { continue; } type = linePoints[i].type; x1 = linePoints[i].x; y1 = linePoints[i].y; v1 = vectors[i].x; v2 = vectors[i].y; switch (type) { case 'L': // get x1, x2, v1, x2 line.setLine(x_offset + (x1 + multipleSize * v1)*zoom, y_offset - (y1 + multipleSize * v2)*zoom, x_offset + (x1 - multipleSize * v1)*zoom, y_offset - (y1 - multipleSize * v1)*zoom); painter.drawLine(line); break; case 'R': // get x1, x2, v1, x2 line.setLine(x_offset + (x1 + multipleSize * v1)*zoom, y_offset - (y1 + multipleSize * v2)*zoom, x_offset + x1*zoom, y_offset - y1*zoom); painter.drawLine(line); break; case 'S': // get x1, x2, v1, x2 line.setLine(x_offset + (x1 + v1)*zoom, y_offset - (y1 + v2)*zoom, x_offset + x1*zoom, y_offset - y1*zoom); painter.drawLine(line); break; default: break; } } for (Circle item : intersection->getCircles()) { if (!item.isExist) { continue; } x1 = item.center.x; y1 = item.center.y; radius = item.radius; circle.setRect(x_offset + (x1 - radius)*zoom, y_offset - (y1 + radius)*zoom, 2*radius*zoom, 2*radius*zoom); painter.drawEllipse(circle); } // 画交点 QPen dotPen; dotPen.setWidth(4); dotPen.setColor(Qt::red); painter.setPen(dotPen); // 遍历交点 for (Point p : intersection->getIntersects()) { x1 = p.x; y1 = p.y; QPointF point(x_offset + x1*zoom, y_offset - y1*zoom); painter.drawPoint(point); } } -
功能展示
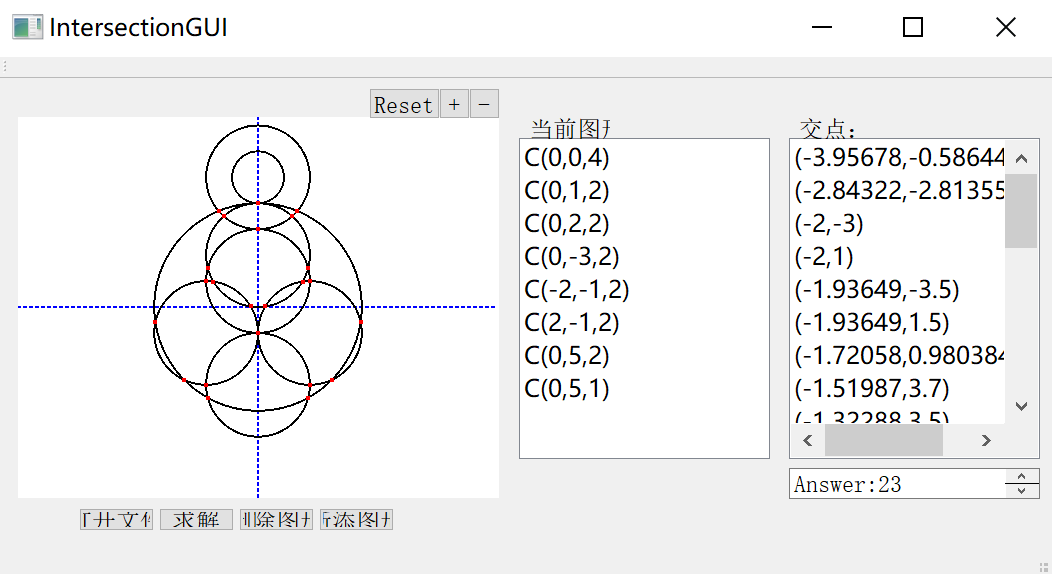
我们的GUI支持从文件导入、求解以及删除图形,同时还支持对于显示窗口的缩放,可以点击+-按钮进行zoom in和zoom out,reset可以恢复默认比例。
![]()
从文件中加载图形信息:
![openFile.gif]()
增加删除元素:
![addAndDel.gif]()
鼠标滚轮放大缩小与移动:
![zoom.gif]()
界面模块与计算模块的对接
如前文所述,我们整个的工程可以分为三个主要部分:
- Intersection:这一部分封装了核心core。
- IntersectionCLI:将core与命令行结合,提供命令行输入输出。
- IntersectionGUI:将core与GUI结合,提供GUI使用。
在GUI中,首先构造一个Intersection类的对象实例,然后通过调用其各种方法来实现相关功能。
ui.setupUi(this);
Intersection* intersection = new Intersection();
然后在打开文件时,我们使用其getAllPoint()方法,结合QFileDialog,弹出窗口进行文件读取:
void IntersectionGUI::openFile(void) {
QString filePath = QFileDialog::getOpenFileName(this, "Open File to Load", "./");
QFileInfo fileInfo = QFileInfo(filePath);
string file_path = fileInfo.absoluteFilePath().toStdString();
ifstream in(file_path);
intersection->getAllPoints(in);
QStringList strList;
loadShape(strList);
ui.allShapes->addItems(strList);
}
类似地,在获取结果是也是同样,调用solveIntersection()方法。
void IntersectionGUI::getResult(void) {
int res = intersection->solveIntersection();
ui.pointNumResult->setText(QString::number(res, 10));
}
我们在绘图时直接使用QPainter,并将其与QW控件进行连接。其中在进行显示时使用Intersection类中的get方法,获取各个图形集合并进行绘制。
完成上述内容后,将各个控件的信号与槽函数进行连接。
connect(ui.openFileButton, SIGNAL(clicked()), this, SLOT(openFile()));
connect(ui.getResult, SIGNAL(clicked()), this, SLOT(getResult()));
connect(ui.deleteShape, SIGNAL(clicked()), this, SLOT(deleteItem()));
connect(ui.draw, SIGNAL(clicked()), this, SLOT(paintItems(ui.canvas)));
描述结对的过程
我们主要使用VS的Live Share以及微信语音进行结对编程。
结对编程的优点和缺点
- 优点
- 结对编程时,双方能够实时对代码进行复核,在调试中出现bug的几率比单人编程或者合作式编程概率要低。而且因为我们是共同设计的,所以不存在一个人只了解一部分代码的情况,两个人对整个程序的代码都比较清楚,在找bug时也能快很多。
- 结对编程是一个学习的好机会。在这次结对时,我也学习了结对对方的设计思路,学习了如何通过改进设计提高运行效率,同时也学会了一些GUI的设计。
- 缺点
- 因为即使一个人不编码做“领航员”也要时刻检查“驾驶员”的代码,因此对于每个人而言可能会花费更多的时间。
- 结对时如果遇到一个人在查资料的时候,可能会造成另一方的时间浪费。所以要想进行高效的结对编程,应当是两个人对一个问题的思路比较清楚,同时对于其实现方法也要能够大体掌握。伙伴
结对双方的优点和缺点
- 结对伙伴
- 优点
- 设计、编码能力都很强
- 工作效率很高
- 能够进行比较有效的沟通
- 缺点
- 有时候会肝得比较晚(捂脸)
- 优点
- 我
- 优点
- 能够根据需要查找资料
- 喜欢学习一些新的东西
- 能够进行比较有效的沟通
- 缺点
- 缺乏行动力
- 写代码的速度比较慢
- 优点



 浙公网安备 33010602011771号
浙公网安备 33010602011771号