【Tensorflow深度学习】线性回归——梯度下降法

线性模型实战——玩具样例（Toy Example）

对于已知真实模型的玩具样例(Toy Example)，我们直接从指定的𝑤 = 1.477 , 𝑏 = 0.089 的真实模型中直接采样：

y=1.477x+0.089

 

1、采样数据

data = []# 保存样本集的列表
for i in range(100): # 循环采样 100 个点
    x = np.random.uniform(-10., 10.) # 随机采样输入 x
    # 采样高斯噪声
    eps = np.random.normal(0., 0.01)
     # 得到模型的输出
    y = 1.477 * x + 0.089 + eps
    data.append([x, y]) # 保存样本点
data = np.array(data)

2、计算误差

def mse(b, w, points):
     # 根据当前的 w,b 参数计算均方差损失
     totalError = 0
     for i in range(0, len(points)): # 循环迭代所有点
         x = points[i, 0] # 获得 i 号点的输入 x
         y = points[i, 1] # 获得 i 号点的输出 y
         # 计算差的平方，并累加
         totalError += (y - (w * x + b)) ** 2
         # 将累加的误差求平均，得到均方差
     return totalError / float(len(points))

3、计算梯度

数学推导：

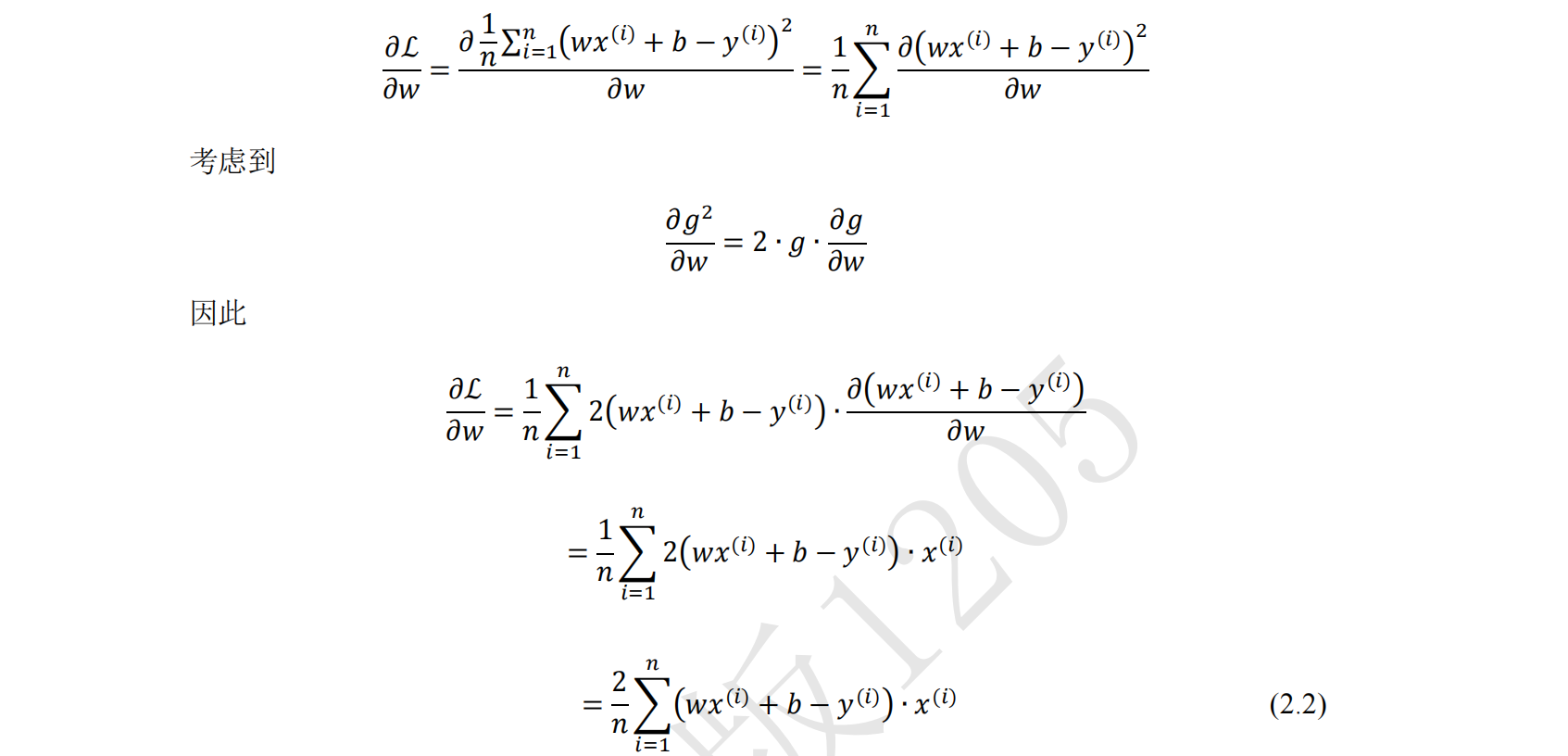
def step_gradient(b_current, w_current, points, lr):
     # 计算误差函数在所有点上的导数，并更新 w,b
     b_gradient = 0
     w_gradient = 0
     M = float(len(points)) # 总样本数
     for i in range(0, len(points)):
         x = points[i, 0]
         y = points[i, 1]
         # 误差函数对 b 的导数：grad_b = 2(wx+b-y)，参考公式(2.3)
         b_gradient += (2/M) * ((w_current * x + b_current) - y)
         # 误差函数对 w 的导数：grad_w = 2(wx+b-y)*x，参考公式(2.2)
         w_gradient += (2/M) * x * ((w_current * x + b_current) - y)
     # 根据梯度下降算法更新 w',b',其中 lr 为学习率
     new_b = b_current - (lr * b_gradient)
     new_w = w_current - (lr * w_gradient)
     return [new_b,new_w]

4、梯度更新

def gradient_descent(points, starting_b, starting_w, lr, num_iterations):
     # 循环更新 w,b 多次
     b = starting_b # b 的初始值
     w = starting_w # w 的初始值
     # 根据梯度下降算法更新多次
    for step in range(num_iterations):
         # 计算梯度并更新一次
         b, w = step_gradient(b, w, np.array(points), lr)
         loss = mse(b, w, points) # 计算当前的均方差，用于监控训练进度
         if step%50 == 0: # 打印误差和实时的 w,b 值
             print(f"iteration:{step}, loss:{loss}, w:{w}, b:{b}")
    return [b, w] # 返回最后一次的 w,b

5、主函数训练如下：

def main():
    # 加载训练集数据，这些数据是通过真实模型添加观测误差采样得到的
    lr = 0.01 # 学习率
    initial_b = 0 # 初始化 b 为 0
    initial_w = 0 # 初始化 w 为 0
    num_iterations = 1000
    # 训练优化 1000 次，返回最优 w*,b*和训练 Loss 的下降过程
    [b, w]= gradient_descent(data, initial_b, initial_w, lr, num_iterations)
    loss = mse(b, w, data) # 计算最优数值解 w,b 上的均方差
    print(f'Final loss:{loss}, w:{w}, b:{b}')