进制表示-03 浮点数-随笔
未来可期
昨天看了很多软考心得,有些博主让我钦佩不已,同时也体现出这一段路不好走,
对于软考架构也有了一定的了解\(\Longrightarrow\)程序员(初级)\(\Longrightarrow\)软件设计师(中级)\(\Longrightarrow\)系统架构设计师(高级)
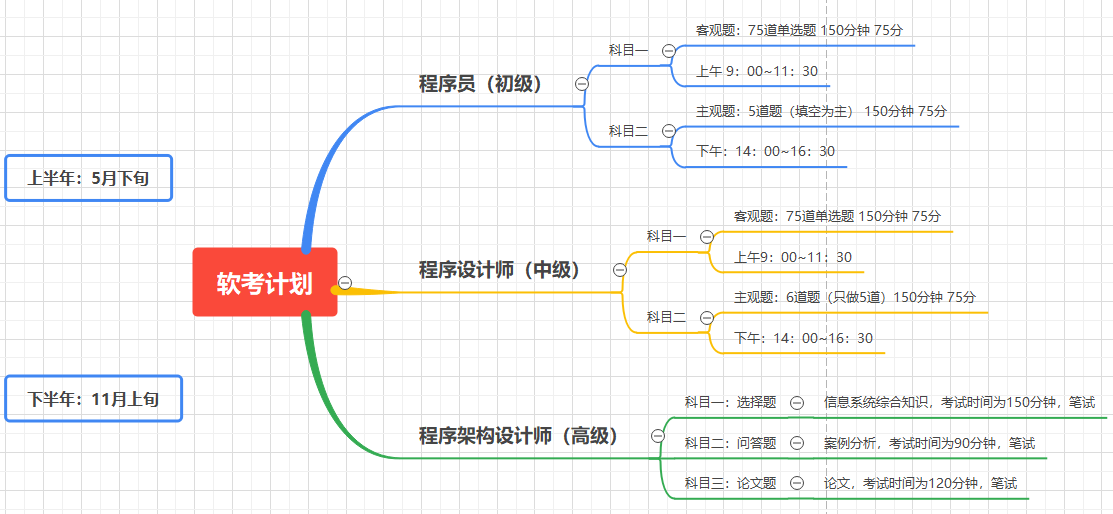
思维导图
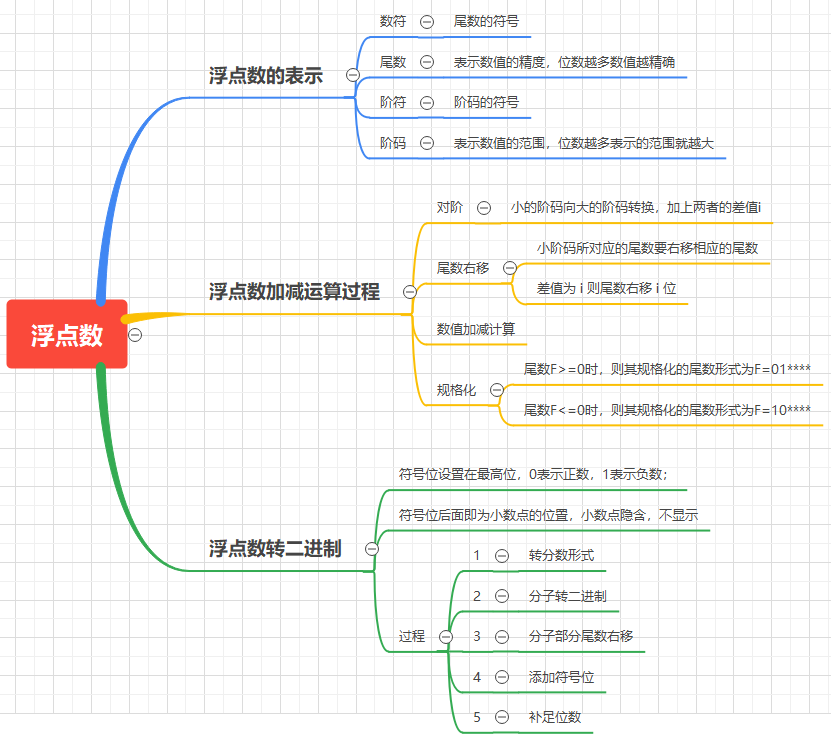
浮点数
- 特点:
1、阶码的位数决定数的表示范围,位数越多范围越大
2、位数的位数决定数的有效精度,位数越多精度越高 - 两浮点数加减运算过程
1、对阶
2、尾数计算
3、结果格式化
注意
1、对阶时,小数向大数看齐(统一规范)
2、对接是通过较小数的尾数右移实现的
软考真题
- 一、-37/64采用8位定点机器码表示
注意步骤:
1、转分数形式
2、分子转二进制
3、分子部分尾数右移
4、添加符号位
5、补足位数
答:
1、-37/\(2^6\)
2、\((2^5 + 2^2 + 2^0) \times2 ^{-6}\)
3、100101\(2 ^{-6}\)
4、1.1001010(1是符号位,结尾不够8位补了0)
- 二、以下关于浮点数表示的叙述中,正确的是(A)。32位浮点数,若阶码采用补码表示,为8为(含1位阶符),尾数采用原码表示,为24位(含1位数符),不考虑格式化,阶码的最大值为(C)
| A、255 | B、256 | C、127 | D、128 |
|---|
- 三、对于浮点数x=\(m^*2^i\) 和y=\(w^*2^j\);已知i>j,那么进行x+y运算时,首先应该对阶,即 (D),使其阶相同
思路:1、对阶:小数->大数;2、j变成i,增加了i-j个
- 四、已知X=-79/128,若采用8位定点机器码表示,则[X]补= (C)
答:
X=-79/\(2^7\)
=\((2^6 + 2^3 + 2^2 + 2^1 +2^0) \times 2^{-7}\)
=1001111\(\times 2^{-7}\)
=.1001111\(\times 2^0\)
=1.1001111(补符号,刚好8位不用补位数);还没完呢,注意看题目,要求补码,咱们现在是原码;转换补码需要的步骤是 原码->反码->补码
=1.0110000 (现在等于反码->再+1就等于补码啦!)
=1.0110001


