深度SVG路径path的贝塞尔曲线指令
贝塞尔曲线
贝塞尔曲线就是这样的一条曲线,它是依据四个位置任意的点坐标绘制出的一条光滑曲线;可以绘制任何曲线,自然包括直线。包括了很多种类型:线性贝塞尔曲线、二次方贝塞尔曲线、三次方贝塞尔曲线、四次方贝塞尔曲线、五次方贝塞尔曲线、……。
直观感受:
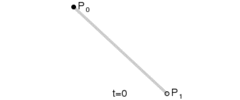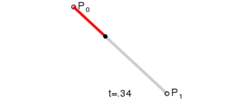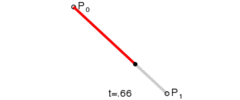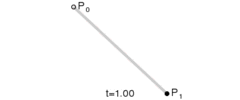
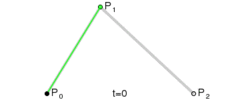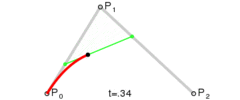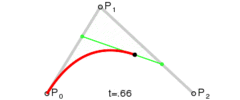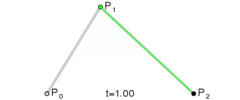
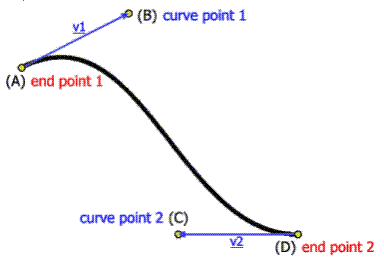
一个标准的3次贝塞尔曲线需要4个点:起始点、终止点(也称锚点)以及两个相互分离的中间点。
三次贝塞尔曲线指令对应指令C,S【厕所】。
- C = curveto
- S = smooth curveto
三次贝塞尔曲线指令:C x1 y1, x2 y2, x y两个控制点(x1,y1)和(x2,y2),(x,y)代表曲线的终点。字母C表示特定动作与行为,这里需要大写,表示标准三次方贝塞尔曲线。
Eg:
1 2 3 4 5 6 7 8 9 10 11 | <svg width="190px" height="160px"> <path d="M10 10 C 20 20, 40 20, 50 10" stroke="3" fill="none"/> <path d="M70 10 C 70 20, 120 20, 120 10" stroke="3" fill="none"/> <path d="M130 10 C 120 20, 180 20, 170 10" stroke="3" fill="none"/> <path d="M10 60 C 20 80, 40 80, 50 60" stroke="3" fill="none"/> <path d="M70 60 C 70 80, 110 80, 110 60" stroke="3" fill="none"/> <path d="M130 60 C 120 80, 180 80, 170 60" stroke="3" fill="none"/> <path d="M10 110 C 20 140, 40 140, 50 110" stroke="3" fill="none"/> <path d="M70 110 C 70 140, 110 140, 110 110" stroke="3" fill="none"/> <path d="M130 110 C 120 140, 180 140, 170 110" stroke="3" fill="none"/></svg> |
图形效果类似:

可以看到M后面的起点,加C后面3个点,构成了贝赛尔曲线的4个点。
C指令有三个坐标参数,而S指令自动对称一个控制点,因此,跟在C指令之后的S指令,只需要2个参数哦,如下:
1 | S x2 y2, x y |

二次贝塞尔曲线指令对应了Q,T【切图】。
- Q = quadratic Belzier curve
- T = smooth quadratic Belzier curveto
二次贝塞尔曲线指令和三次贝塞尔曲线相比,就是2个控制点合为1个。

参考:
贝塞尔曲线百度百科:
http://baike.baidu.com/link?url=GJdFZM4ZYyML_KeohngfW40eKL85UTpTSmi4UYyLG1mBluQq3U8ZskDHu-k_gK_hD1Mk86xRFuvKQJ6QOE3wWa
深度SVG路径path的贝塞尔曲线指令
http://www.zhangxinxu.com/wordpress/2014/06/deep-understand-svg-path-bezier-curves-command/
贝塞尔曲线初探
http://www.cnblogs.com/jay-dong/archive/2012/09/26/2704188.html
Animated Bézier Curves
https://www.jasondavies.com/animated-bezier/



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 深入理解 Mybatis 分库分表执行原理
· 如何打造一个高并发系统?
· .NET Core GC压缩(compact_phase)底层原理浅谈
· 现代计算机视觉入门之:什么是图片特征编码
· .NET 9 new features-C#13新的锁类型和语义
· Sdcb Chats 技术博客:数据库 ID 选型的曲折之路 - 从 Guid 到自增 ID,再到
· 语音处理 开源项目 EchoSharp
· 《HelloGitHub》第 106 期
· Spring AI + Ollama 实现 deepseek-r1 的API服务和调用
· 使用 Dify + LLM 构建精确任务处理应用