函数
一、函数声明:
(1)函数声明由函数返回类型、函数名和形参列表组成,这三个元素被称为函数原型;
(2)如果函数定义和函数声明只有返回类型不一致,编译器会出错,属于同一声明;
(3)函数声明中的形参名会被忽略;
(4)函数一般在头文件中声明,然后在源文件中进行定义;
(5)如果声明两个函数void fun(inta)与void fun(const int a),会发生编译错误,认为是重复声明,因为这两个函数可以传递的实参类型完全一样;
二、函数返回:
(1)函数必须指定返回类型,函数不能返回另一个函数或者内置数组类型,但是可以返回函数指针和指向数组元素的指针;
(2)返回类型不是void的函数必须返回(return)一个值,一个特例就是:容许主函数main没有return语句就结束,默认返回0。如果在if语句里进行函数返回,并不需要每个分支都有return返回,只要有return语句就可以通过编译;
三、函数的参数传递:
(1)值传递是指发生函数调用时,给形参分配内存空间,并用实参来初始化形参。这一过程是参数值单向传递的过程,一旦形参获得了值便与实参脱离了关系,此后无论形参发生了怎样的改变,都不会影响实参。
(2)引用传递:引用是一种特殊类型的变量,可以被认为是另一个变量的别名,通过引用名和通过被引用的变量名访问变量效果是一样的。
注:声明一个引用时,必须同时对它进行初始化,使它指向一个已存在的对象;一旦一个引用被初始化后,就不能改为指向其他对象。
四、函数重载:
(1)两个以上的函数,具有相同的函数名,但是形参的个数或者类型不同,编译器根据实参和形参的类型及个数的最佳匹配,自动确定调用哪一个函数,这就是函数的重载。
(2)重载函数的形参必须不同,个数或类型不同,编译程序进行最佳匹配,来选择调用哪一个函数。如果函数名相同,形参类型也相同,在编译时会被认为是语法错误。
五、其它注意点:
(1)内联函数不是在调用时发生控制转移,而是在编译时将函数嵌入在每一个调用处。通常使用于简单且常被调用的函数,类似于C语言的宏定义。
(2)函数在定义时可以预先声明默认的形参值。有默认值的形参必须在形参列表的最后。在相同的作用域内,不允许在同一个函数的多个声明中对同一个参数的默认值重复定义,即前后定义的值相同也不行。
六、例题练习。
1.例3-2 输入一个8位二进制数,将其转换为十进制数输出。
分析:将二进制数转换为十进制数的过程包括求2的N次方和与权值相乘并求和的过程,通过power函数来求2的N次方,power函数定义位于调用之后因此要事先声明。
Code:
#include<iostream>
using namespace std;
double power(double x,int n);
int main(){
int value=0;
cout<<"Enter an 8 bit binary number: ";
for(int i=7;i>=0;i--){
char ch;
cin>>ch;
if(ch=='1')
value+=static_cast<int>(power(2,i));
}
cout<<"Decimal value is "<<value<<endl;
return 0;
}
double power(double x,int n){
double val=1.0;
while(n--)
val*=x;
return val;
}
运行结果:

2编写程序求π值,公式如下。
π=16arctan(1/5)-4arctan(1/239)
其中arctan用如下形式的级数计算:
Arctanx=x-x^3/3+x^5/5-x^7/7+…
分析:在该例中,公式均已经给出,代码仅需要实现arctan级数计算,再代入公式即可,观察arctan的形式,发现每一项正负交错,系数为奇数依次递增,即每个数比前一个数大2,而x得次数也是以2次递增,因此设定了sqr为x*x,i+=2,而正负号得变化通过判定实现,容易发现4作为条件可以对半依次区分出正负号。
Code:
#include<iostream>
using namespace std;
double arctan(double x){
double sqr=x*x;
double e=x;
double r=0;
int i=1;
while(e/i>1e-15){
double f=e/i;
r=(i%4==1)?r+f:r-f;
e=e*sqr;
i+=2;
}
return r;
}
int main(){
double a=16.0*arctan(1/5.0);
double b=4.0*arctan(1/239.0);
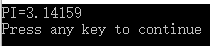
cout<<"PI="<<a-b<<endl;
return 0;
}
运行结果:
3例3-10 汉诺塔问题
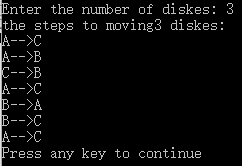
有三根针A,B,C。A针上有n个盘子,盘子大小不等,大的在下,小的在上。要求把这n个盘子从A针移到C针,在移动过程中可借助B针,每次只允许动一个盘,且在移动过程中在三根针上都保持大盘在下,小盘在上。
分析:将n个盘子从A针移动到C针分为3个步骤,首先将A上n-1个盘子通过C针移动到B针,再把A针最后一个盘子移动到C,最后将B上的n-1个盘子通过A针移动到C针。通过hanoi函数的递归实现。
Code:
#include<iostream>
using namespace std;
void move(char src,char dest){
cout<<src<<"-->"<<dest<<endl;
}
void hanoi(int n,char src, char medium, char dest){
if(n==1)
move(src,dest);
else{
hanoi(n-1,src,dest,medium);
move(src,dest);
hanoi(n-1,medium,src,dest);
}
}
int main(){
int m;
cout<<"Enter the number of diskes: ";
cin>>m;
cout<<"the steps to moving"<<m<<" diskes:"<<endl;
hanoi(m,'A','B','C');
return 0;
}
运行结果:
4.例3-16 重载函数应用举例。
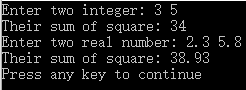
编写两个名为sumOfSquare的重载函数,分别求两整数的平方和及两实数的平方和。
Code:
#include<iostream>
using namespace std;
int sumOfSquare(int a,int b){
return a*a+b*b;
}
double sumOfSquare(double a,double b){
return a*a+b*b;
}
int main(){
int m,n;
cout<<"Enter two integer: ";
cin>>m>>n;
cout<<"Their sum of square: "<<sumOfSquare(m,n)<<endl;
double x,y;
cout<<"Enter two real number: ";
cin>>x>>y;
cout<<"Their sum of square: "<<sumOfSquare(x,y)<<endl;
return 0;
}
运行结果: