对《禁忌搜索(Tabu Search)算法及python实现》的修改
这个算法是在听北大人工智能mooc的时候,老师讲的一种局部搜索算法,可是举得例子不太明白。搜索网页后,发现《禁忌搜索(Tabu Search)算法及python实现》(https://blog.csdn.net/adkjb/article/details/81712969) 已经做了好详细的介绍,仔细看了下很有收获。于是想泡泡代码,看前面还好,后边的代码有些看不懂了,而且在函数里定义函数,这种做法少见,并且把函数有当作类来用,为什么不直接用类呢。还有就是,可能对禁忌搜索不太了解,可能具体算法在代码里有问题,欢迎提出。
import random class Tabu: def __init__(self,tabulen=100,preparelen=200): self.tabulen=tabulen self.preparelen=preparelen self.city,self.cityids,self.stid=self.loadcity2() #我直接把他的数据放到代码里了 self.route=self.randomroute() self.tabu=[] self.prepare=[] self.curroute=self.route.copy() self.bestcost=self.costroad(self.route) self.bestroute=self.route def loadcity(self,f="d:/Documents/code/aiclass/tsp.txt",stid=1): city = {} cityid=[] for line in open(f): place,lon,lat = line.strip().split(" ") city[int(place)]=float(lon),float(lat) #导入城市的坐标 cityid.append(int(place)) return city,cityid,stid def loadcity2(self,stid=1): city={1: (1150.0, 1760.0), 2: (630.0, 1660.0), 3: (40.0, 2090.0), 4: (750.0, 1100.0), 5: (750.0, 2030.0), 6: (1030.0, 2070.0), 7: (1650.0, 650.0), 8: (1490.0, 1630.0), 9: (790.0, 2260.0), 10: (710.0, 1310.0), 11: (840.0, 550.0), 12: (1170.0, 2300.0), 13: (970.0, 1340.0), 14: (510.0, 700.0), 15: (750.0, 900.0), 16: (1280.0, 1200.0), 17: (230.0, 590.0), 18: (460.0, 860.0), 19: (1040.0, 950.0), 20: (590.0, 1390.0), 21: (830.0, 1770.0), 22: (490.0, 500.0), 23: (1840.0, 1240.0), 24: (1260.0, 1500.0), 25: (1280.0, 790.0), 26: (490.0, 2130.0), 27: (1460.0, 1420.0), 28: (1260.0, 1910.0), 29: (360.0, 1980.0)} #原博客里的数据 cityid=list(city.keys()) return city,cityid,stid def costroad(self,road): #计算当前路径的长度 与原博客里的函数功能相同 d=-1 st=0,0 cur=0,0 city=self.city for v in road: if d==-1: st=city[v] cur=st d=0 else: d+=((cur[0]-city[v][0])**2+(cur[1]-city[v][1])**2)**0.5 #计算所求解的距离,这里为了简单,视作二位平面上的点,使用了欧式距离 cur=city[v] d+=((cur[0]-st[0])**2+(cur[1]-st[1])**2)**0.5 return d def randomroute(self): #产生一条随机的路 stid=self.stid rt=self.cityids.copy() random.shuffle(rt) rt.pop(rt.index(stid)) rt.insert(0,stid) return rt def randomswap2(self,route): #随机交换路径的两个节点 route=route.copy() while True: a=random.choice(route) b=random.choice(route) if a==b or a==1 or b==1: continue ia=route.index(a) ib=route.index(b) route[ia]=b route[ib]=a return route def step(self): #搜索一步路找出当前下应该搜寻的下一条路 rt=self.curroute i=0 while i<self.preparelen: #产生候选路径 prt=self.randomswap2(rt) if int(self.costroad(prt)) not in self.tabu: #产生不在禁忌表中的路径 self.prepare.append(prt.copy()) i+=1 c=[] for r in self.prepare: c.append(self.costroad(r)) mc=min(c) mrt=self.prepare[c.index(mc)] #选出候选路径里最好的一条 if mc<self.bestcost: self.bestcost=mc self.bestroute=mrt.copy() #如果他比最好的还要好,那么记录下来 self.tabu.append(mc)#int(mrt)) #这里本来要加 mrt的 ,可是mrt是路径,要对比起来麻烦,这里假设每条路是由长度决定的 #也就是说 每个路径和他的长度是一一对应,这样比对起来速度快点,当然这样可能出问题,更好的有待研究 self.curroute=mrt #用候选里最好的做下次搜索的起点 self.prepare=[] if len(self.tabu)>self.tabulen: self.tabu.pop(0)
下面跑跑看:
import timeit
t=Tabu()print('ok') print(t.city) print(t.route) print(t.bestcost) print(t.curroute) for i in range(1000): t.step() if i%50==0: print(t.bestcost) print(t.bestroute) print(t.curroute) print('ok') #print(timeit.timeit(stmt="t.step()", number=1000,globals=globals())) print('ok')
ok
{1: (1150.0, 1760.0), 2: (630.0, 1660.0), 3: (40.0, 2090.0), 4: (750.0, 1100.0), 5: (750.0, 2030.0), 6: (1030.0, 2070.0), 7: (1650.0, 650.0), 8: (1490.0, 1630.0), 9: (790.0, 2260.0), 10: (710.0, 1310.0), 11: (840.0, 550.0), 12: (1170.0, 2300.0), 13: (970.0, 1340.0), 14: (510.0, 700.0), 15: (750.0, 900.0), 16: (1280.0, 1200.0), 17: (230.0, 590.0), 18: (460.0, 860.0), 19: (1040.0, 950.0), 20: (590.0, 1390.0), 21: (830.0, 1770.0), 22: (490.0, 500.0), 23: (1840.0, 1240.0), 24: (1260.0, 1500.0), 25: (1280.0, 790.0), 26: (490.0, 2130.0), 27: (1460.0, 1420.0), 28: (1260.0, 1910.0), 29: (360.0, 1980.0)}
[1, 6, 2, 12, 9, 28, 15, 21, 8, 22, 29, 19, 26, 24, 20, 18, 17, 7, 4, 16, 27, 11, 14, 25, 10, 3, 13, 23, 5]
24651.706120672443
[1, 6, 2, 12, 9, 28, 15, 21, 8, 22, 29, 19, 26, 24, 20, 18, 17, 7, 4, 16, 27, 11, 14, 25, 10, 3, 13, 23, 5]
21567.36269967159
[1, 6, 2, 12, 9, 28, 15, 21, 8, 22, 29, 3, 26, 24, 20, 18, 17, 7, 4, 16, 27, 11, 14, 25, 10, 19, 13, 23, 5]
[1, 6, 2, 12, 9, 28, 15, 21, 8, 22, 29, 3, 26, 24, 20, 18, 17, 7, 4, 16, 27, 11, 14, 25, 10, 19, 13, 23, 5]
9701.867337779715
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 8, 27, 23, 7, 25, 15, 4, 13, 24]
9701.867337779715
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 12, 6, 5, 9, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 16, 27, 8, 23, 7, 25, 19, 4, 13, 24]
9701.867337779715
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 12, 6, 5, 9, 26, 29, 3, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
9701.867337779715
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 12, 6, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
9667.242844275002
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 6, 12, 9, 3, 29, 26, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 16, 8, 27, 23, 7, 25, 19, 4, 13, 24]
9667.242844275002
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
9667.242844275002
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 6, 12, 9, 5, 26, 29, 3, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
9667.242844275002
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 16, 27, 8, 23, 7, 25, 15, 4, 13, 24]
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 16, 27, 8, 23, 7, 25, 19, 4, 13, 24]
9248.522952771107
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 9, 5, 29, 3, 26, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 19, 15, 4, 13, 16, 25, 7, 23, 8, 27, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 8, 27, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 5, 9, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 6, 12, 9, 5, 29, 3, 26, 21, 2, 20, 10, 18, 17, 14, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 9, 26, 29, 3, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 8, 27, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 9, 5, 26, 29, 3, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 12, 6, 5, 9, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
9213.898459266395
[1, 28, 6, 12, 9, 26, 3, 29, 5, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
[1, 28, 6, 12, 9, 5, 26, 3, 29, 21, 2, 20, 10, 18, 14, 17, 22, 11, 15, 4, 13, 16, 19, 25, 7, 23, 27, 8, 24]
看到最小路径是9213.89 如果我们把timeit去掉,跑1000步我的电脑是不到4秒大概
为了直观把路径画下来:
from matplotlib import pyplot x=[] y=[] print("最优路径长度:",t.bestcost) for i in t.bestroute: x0,y0=t.city[i] x.append(x0) y.append(y0) x.append(x[0]) y.append(y[0]) pyplot.plot(x,y) pyplot.scatter(x,y)
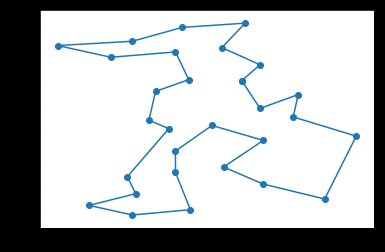
貌似找到最好的了。。。。
再跑一次:
9760.12

再来一次:
10212
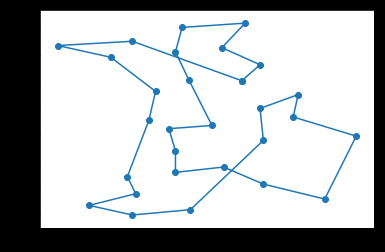
10500
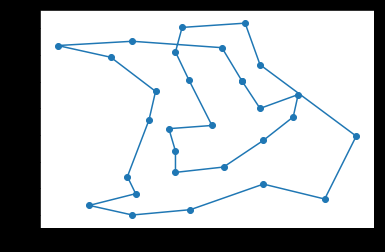
10100
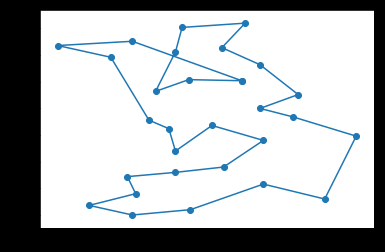
10080
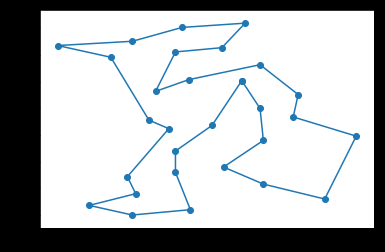
发现有些地方总有不变的地方,是不是可以把多条线路给叠加起来,做个链接的加权图,按照路径的权再来启发,是否能得到更好的结果呢?
比如右下角,一直都是一个形状,是否说明,这几个点的连接状况固定了呢?
这样可以把总是连续的点给合并成一个整体再来搜索是否也是个办法?
CSDN我的博客不知道怎么给禁用了,不能留言给博主,只能这样了。



