《Self-Attention Generative Adversarial Networks》里的注意力计算

前天看了 criss-cross 里的注意力模型  仔细理解了  在： https://www.cnblogs.com/yjphhw/p/10750797.html

 

今天又看了一个注意力模型 《Self-Attention Generative Adversarial Networks》   https://arxiv.org/pdf/1805.08318v1.pdf

里边关键的还是注意力机制，又花了一个小时理解了下，感觉这种方式能够带来另一种视野的扩大，其中cnn是通过不断卷积扩大视野。

而这种注意力模型直接通过内积（矩阵的乘法）和 线性组合来直接获取全局信息，作者们都认为是注意力！ 是否有其他含义还需要进一步理解。

 

这篇文章里关键就是注意力的产生：

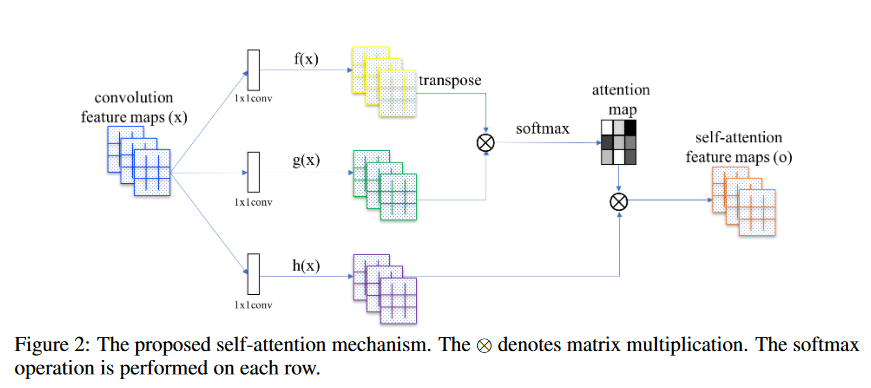
这里边的操作 圆圈里的差  就是值得矩阵乘法。 整个这种注意力机制的论文多起来， 经典的style tranfer的论文也是用类似的方法计算风格损失的 格莱姆矩阵

 

下面就从输入x开始， x是个 c*w*h的 特征图  论文里写 c*n 是因为把w*h 展开了 。

然后三路 1*1卷积，没问题，这个操作可以先不展开。

这里我们用不展开的方式 先描述  f(x)和g(x）做 c`*1*1的卷积， h(x)是 做 c*1*1的卷积

做完后 对f(x),g(x) 在空间维度上拉开 w*h 拉开为 n=w*h  

黄色的就是  c`*n    绿色也是  c`*n      大小的矩阵

对黄色的转置 就是 n*c`    然后 和绿色的就能做矩阵乘法 

得到一个 n*n的矩阵。下边为了归一化参数，在列的方向上做softmax。得到了一个n*n的注意力矩阵，为什么在列方向上归一化，这是因为为了下一步和h(x)的特征图相乘

 

h(x)是经过 c*1*1的卷积操作，对输入x进行了一次变换的来的，同样对其拉开就成了一个 c*n的矩阵

 

刚才得到的注意力矩阵式n*n的，并且在列上归一化了，  所以 h(x)* attention  得到一个  (c*n) *（n*n)= c*n 大小的矩阵。

然后恢复 c*n 到 c*w*h就可以。

这样就可以看到这完全就是对每个位置和所有位置进行加权，一下子具有全局感受视野，而且每个位置的权值不同。

这可以细细体会下，这样的操作到底代表了什么。

卷积是扩大视野的方法，这种操作直接一步到位获取了全局视野。

和criss-cross的方法是在通道上，这个直接是在通道内。不太确定。

之前还有squeeze 和 excitation的注意力方法

如何结合起来，是否可以用在分类上，提升分类精度？ 值得思考。