样本不均衡下的分类损失函数
通常二分类使用交叉熵损失函数,但是在样本不均衡下,训练时损失函数会偏向样本多的一方,造成训练时损失函数很小,但是对样本较小的类别识别精度不高。
解决办法之一就是给较少的类别加权,形成加权交叉熵(Weighted cross entropy loss)。今天看到两个方法将权值作为类别样本数量的函数,其中有一个很有意思就录在这里。

(http://cn.arxiv.org/pdf/1711.05225v3)
上边说明的时,正负样本的权值和他们的对方数量成比例,举个例子,比如正样本有30,负样本有70,那么正样本的权w+=70/(30+70)=0.7,负样本的权就是w-=30/(30+70)=0.3,
这样算下来的权值是归一的。这种方法比较直观,普通,应该是线性的。
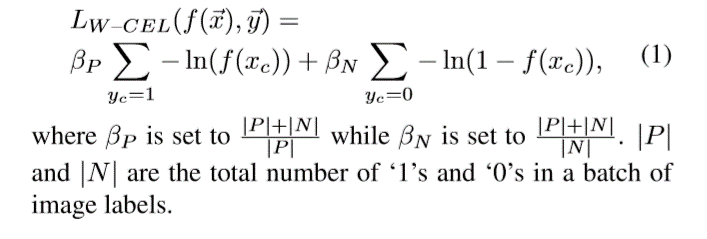
(https://arxiv.org/pdf/1705.02315v4.pdf)
这个的权值直接就是该类别样本数的反比例函数,是非线性的,相比于上边的很有意思,提供了另一种思路。为了统一期间还是使用w+,w-表示这里的beta P和beta N,
举个例子,比如正样本有30,负样本有70,那么正样本的权w+=(30+70)/30=3.33,负样本的权就是w-=(30+70)/70=1.42。
第三中方法:Focal loss
https://www.jianshu.com/p/204d9ad9507f
https://arxiv.org/pdf/1708.02002.pdf
第四种方法:GHM-C loss
https://arxiv.org/pdf/1811.05181.pdf
以后看到后继续补充。



