算法练习(18)-图的拓扑排序

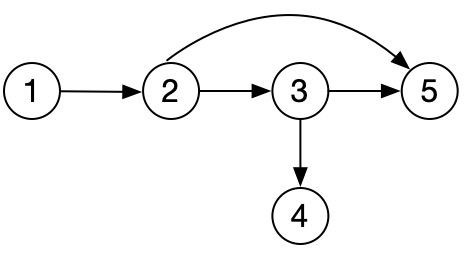
如上图，假设有一个大型代码工程，里面有5个模块：

模块1依赖模块2

模块2依赖模块3和模块5

模块3依赖模块4和模块5

那么，项目在编译时，应该按怎样的的顺序编译? 这就是所谓的拓扑排序问题

就这个示例而言，显然正确的编译顺序是：5->4->3->2->1 或 4->5->3->2->1  (注：4与5之间没有相互依赖，谁先谁后都可以)

 

思路：如下图，先找出入度为0的节点，然后以它为源点，依次把相邻节点的入度减1，然后再以下1个入度为0的点做为起点，依次反复，直到最后所有节点的入度都为0，最后把这个过程中经过的入度为0的点，倒过来，就是正确的顺序。

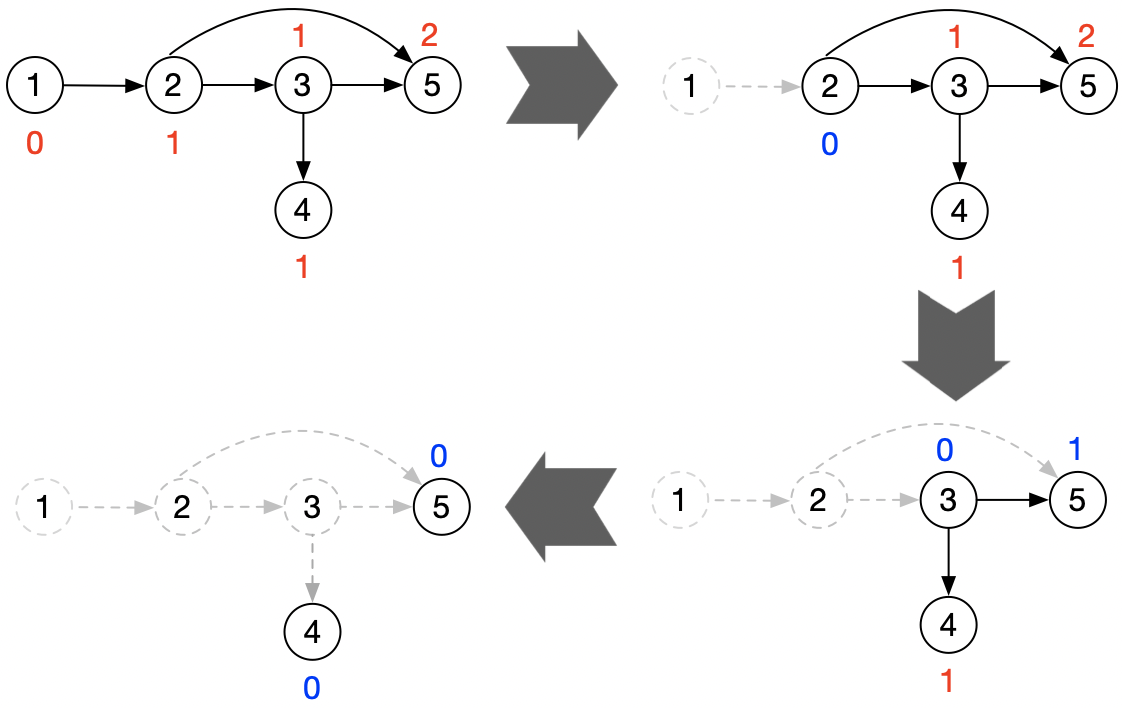
算法并不复杂，但问题在于，如果面试中遇到该题，通常给的输入并非图结构，可能是个二维数据，比如：

        int[][] arr = new int[][]{
                new int[]{1, 2},
                new int[]{2, 5},
                new int[]{2, 3},
                new int[]{3, 4},
                new int[]{3, 5}
        };

第1个数字表示自身，第2个数字表示下1个依赖的节点，这种情况，只要转换成上一篇里的Graph结构即可：

Graph convert(int[][] arr) {
        List<Node> nodes = new ArrayList<>();
        List<Edge> edges = new ArrayList<>();
        HashMap<Integer, Node> map = new HashMap<>();
        for (int[] items : arr) {
            int curVal = items[0];
            int nextVal = items[1];
            Node cur = map.get(curVal);
            Node next = map.get(nextVal);
            if (cur == null) {
                cur = new Node(curVal);
                map.put(curVal, cur);
            }
            if (next == null) {
                next = new Node(nextVal);
                map.put(nextVal, next);
            }
            if (!cur.nexts.contains(next)) {
                cur.nexts.add(next);
                next.in++;
            }
            if (!nodes.contains(cur)) {
                nodes.add(cur);
            }
            if (!nodes.contains(next)) {
                nodes.add(next);
            }
        }
        Graph g = new Graph(nodes, edges);
        return g;
    }

注：本算法中，并不需要用到边Edge，所以上面的转换过程，并没有处理Edge.

接下来，就可以开始搞拓扑排序了：

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Stack;

public class GraphTest {

    Graph convert(int[][] arr) {
        List<Node> nodes = new ArrayList<>();
        List<Edge> edges = new ArrayList<>();
        HashMap<Integer, Node> map = new HashMap<>();
        for (int[] items : arr) {
            int curVal = items[0];
            int nextVal = items[1];
            Node cur = map.get(curVal);
            Node next = map.get(nextVal);
            if (cur == null) {
                cur = new Node(curVal);
                map.put(curVal, cur);
            }
            if (next == null) {
                next = new Node(nextVal);
                map.put(nextVal, next);
            }
            if (!cur.nexts.contains(next)) {
                cur.nexts.add(next);
                next.in++;
            }
            if (!nodes.contains(cur)) {
                nodes.add(cur);
            }
            if (!nodes.contains(next)) {
                nodes.add(next);
            }
        }
        Graph g = new Graph(nodes, edges);
        return g;
    }

    /**
     * 拓扑排序
     *
     * @param g 有向无环图
     * @return
     */
    List<Integer> topologicalSort(Graph g) {
        //找出入度为0的节点
        Node first = null;
        for (Node node : g.nodes) {
            if (node.in == 0) {
                first = node;
                break;
            }
        }

        //相邻节点入度-1, 如减到0，则入栈
        Stack<Node> stack = new Stack<>();
        stack.add(first);
        while (first.nexts.size() != 0) {
            for (Node next : first.nexts) {
                next.in--;
                if (next.in == 0) {
                    stack.add(next);
                    first = next;
                }
            }
        }

        //弹出结果
        List<Integer> list = new ArrayList<>();
        while (!stack.isEmpty()) {
            list.add(stack.pop().value);
        }
        return list;
    }


    public static void main(String[] args) {
        GraphTest t = new GraphTest();
        int[][] arr = new int[][]{
                new int[]{1, 2},
                new int[]{2, 5},
                new int[]{2, 3},
                new int[]{3, 4},
                new int[]{3, 5}
        };
        Graph g = t.convert(arr);
        List<Integer> result = t.topologicalSort(g);
        System.out.println(result);


    }

}

输出：[5, 4, 3, 2, 1]