算法练习(17)-图的广度优先遍历/深度优先遍历

一、图的数据结构及表示法

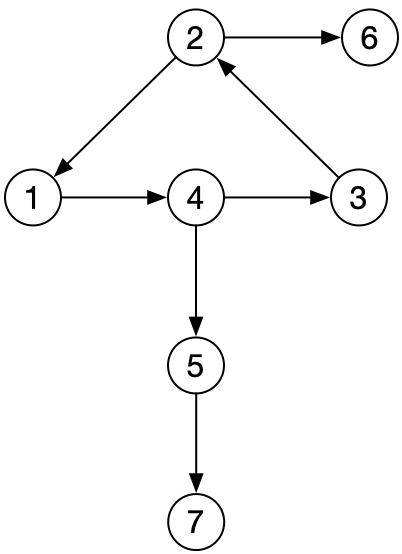
如上图，由一堆"点"与一堆"边"构成的数据结构 ，就称为图，其中边上可以有方向（称为有向图），也可以无方向（称为无向图）。边上还可以有所谓的权重值。

算法书上，图的表示方法一般有“邻接矩阵”等，这里我们用左程云介绍的一种相对更容易理解的表示法：

图：

import java.util.List;

public class Graph {

    //点集
    public List<Node> nodes;

    //边集
    public List<Edge> edges;

    public Graph(List<Node> nodes, List<Edge> edges) {
        this.nodes = nodes;
        this.edges = edges;
    }
}

节点：

import java.util.ArrayList;
import java.util.List;

public class Node {
    public int value;
    //入度(即：有几个节点连到自己)
    public int in;
    //出度(即：对外连到几个其它节点)
    public int out;
    //对外连了哪些相邻节点
    public List<Node> nexts;
    //有几条从自已出发的边
    public List<Edge> edges;

    public Node(int val) {
        this.value = val;
        this.in = 0;
        this.out = 0;
        this.nexts = new ArrayList<>();
        this.edges = new ArrayList<>();
    }
}

注：如果为了调试方便输出，可以加上toString()

//    @Override
//    public String toString() {
//        return "Node{" +
//                "value=" + value +
//                ", in=" + in +
//                ", out=" + out +
//                ", nexts=" + nexts +
//                ", edges=" + edges +
//                '}';
//    }

    @Override
    public String toString() {
        return value + "";
    }

边：

public class Edge {
    public Node from;
    public Node to;
    public int weight = 0;

    public Edge(int weight, Node from, Node to) {
        this.weight = weight;
        this.from = from;
        this.to = to;
    }
}

最开始那张图，就可以类似下面的代码来构建：

public Graph initGraph() {
        Node n1 = new Node(1);
        Node n2 = new Node(2);
        Node n3 = new Node(3);
        Node n4 = new Node(4);
        Node n5 = new Node(5);
        Node n6 = new Node(6);
        Node n7 = new Node(7);

        n1.in = 1;
        n1.out = 1;
        n1.nexts.add(n4);
        n1.edges.add(new Edge(0, n1, n4));

        n6.in = 1;

        n2.in = 1;
        n2.out = 2;
        n2.nexts.add(n1);
        n2.nexts.add(n6);
        n2.edges.add(new Edge(0, n2, n1));
        n2.edges.add(new Edge(0, n2, n6));

        n3.in = 1;
        n3.out = 1;
        n3.nexts.add(n2);
        n3.edges.add(new Edge(0, n3, n2));

        n5.in = 1;
        n5.out = 1;
        n5.nexts.add(n7);
        n5.edges.add(new Edge(0, n5, n7));

        n4.in = 1;
        n4.out = 2;
        n4.nexts.add(n3);
        n4.nexts.add(n5);
        n4.edges.add(new Edge(0, n4, n3));
        n4.edges.add(new Edge(0, n4, n5));


        List<Node> nodes = new ArrayList<>();
        nodes.add(n1);
        nodes.add(n2);
        nodes.add(n3);
        nodes.add(n4);
        nodes.add(n5);
        nodes.add(n6);
        nodes.add(n7);

        List<Edge> edges = new ArrayList<>();
        edges.addAll(n1.edges);
        edges.addAll(n2.edges);
        edges.addAll(n3.edges);
        edges.addAll(n4.edges);
        edges.addAll(n5.edges);
        edges.addAll(n6.edges);
        edges.addAll(n7.edges);

        Graph g = new Graph(nodes, edges);

        return g;
    }

　　

二、广度优先遍历

思路：从源节点开始（注：假设源节点不是有进无出的终止节点），依次遍历自己相邻的节点，这里要注意下，如果图中有环，不要形成死循环。

    /**
     * breadth-first search
     * @param g
     */
    void bfs(Graph g) {
        if (g == null || g.nodes == null || g.nodes.size() == 0) {
            return;
        }

        Node n = g.nodes.get(0);
        Queue<Node> queue = new LinkedList<>();
        //用于辅助判断，节点是否已经遍历过，防止有环情况下，形成死循环
        Set<Node> set = new HashSet<>();
        queue.add(n);
        set.add(n);

        while (!queue.isEmpty()) {
            Node curr = queue.poll();
            System.out.printf(curr.value + " ");
            for (Node next : curr.nexts) {
                if (!set.contains(next)) {
                    queue.add(next);
                    set.add(next);
                }
            }
        }
    }

以本文最开始的图为例，输出为：1 4 3 5 2 7 6 

　　

三、深度优先遍历

思路：与广度优先不同，深度优先要沿着某个节点，尽可能向纵深走，而非优先看自身相邻节点，这里要换成Stack，而非Queue，详见下面的代码

/**
     * depth-first search 深度优先遍历
     *
     * @param g
     */
    void dfs(Graph g) {
        if (g == null || g.nodes == null || g.nodes.size() == 0) {
            return;
        }

        Node n = g.nodes.get(0);
        Stack<Node> stack = new Stack<>();
        //用于辅助判断，节点是否已经遍历过，防止有环情况下，形成死循环
        Set<Node> set = new HashSet<>();
        stack.add(n);
        set.add(n);

        System.out.printf(n.value + " ");
        while (!stack.isEmpty()) {
            //先把自己弹出来
            Node curr = stack.pop();
            for (Node next : curr.nexts) {
                if (!set.contains(next)) {
                    //再把自己及下1个节点压进去
                    //由于stack是先进后出，
                    //所以弹出的顺序就变成了 下一个节点（即：更深层的）先弹出
                    //从而达到了深度优先的效果
                    stack.add(curr);
                    stack.add(next);
                    set.add(next);
                    System.out.printf(next.value + " ");
                    break;
                }
            }
        }
    }

输出结果：1 4 3 2 6 5 7

 

四、带权重的遍历

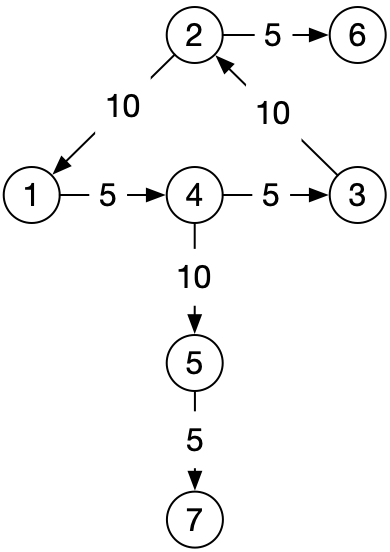
比如上图，如果边上有权重值，假设权重值越大，优先级越高，那么只要把上述的代码略做调整，在入队/入栈时，按权重排下序即可

带权重的广度优先遍历：

    /**
     * 带权重的breadth-first search
     *
     * @param g
     */
    void bfs2(Graph g) {
        if (g == null || g.nodes == null || g.nodes.size() == 0) {
            return;
        }

        Node n = g.nodes.get(0);
        Queue<Node> queue = new LinkedList<>();
        //用于辅助判断，节点是否已经遍历过，防止有环情况下，形成死循环
        Set<Node> set = new HashSet<>();
        queue.add(n);
        set.add(n);

        while (!queue.isEmpty()) {
            Node curr = queue.poll();
            System.out.printf(curr.value + " ");
            //根据边上的权重值排序
            curr.edges.sort((o1, o2) -> o1.weight < o2.weight ? 1 : -1);
            for (Edge next : curr.edges) {
                if (!set.contains(next.to)) {
                    queue.add(next.to);
                    set.add(next.to);
                }
            }
        }
    }

输出：1 4 5 3 7 2 6

　

带权重的深度优先遍历：

/**
     * 带权重的深度优先遍历(菩提树下的杨过 yjmyzz.cnblogs.com)
     * @param g
     */
    void dfs2(Graph g) {
        if (g == null || g.nodes == null || g.nodes.size() == 0) {
            return;
        }

        Node n = g.nodes.get(0);
        Stack<Node> stack = new Stack<>();
        Set<Node> set = new HashSet<>();
        stack.add(n);
        set.add(n);

        System.out.printf(n.value + " ");
        while (!stack.isEmpty()) {
            Node curr = stack.pop();
            //根据边上的权重值排序
            curr.edges.sort((o1, o2) -> o1.weight < o2.weight ? 1 : -1);
            for (Edge next : curr.edges) {
                if (!set.contains(next.to)) {
                    stack.add(curr);
                    stack.add(next.to);
                    set.add(next.to);
                    System.out.printf(next.to.value + " ");
                    break;
                }
            }
        }
    }

输出：1 4 5 7 3 2 6

 

五、无向图的处理

对于无向图而言，可以看成是有向图的特例：

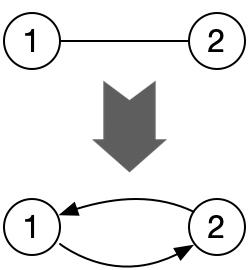
如上图，节点1与节点2构成了1张最简单的图，从1可以走到2，从2也可以走到1，可以理解为1与2之间，各有一条指向对方的边，用代码表示的话，类似下面这样：

    public Graph buildGraph() {
        Node n1 = new Node(1);
        Node n2 = new Node(2);

        n1.out = 2;
        n1.in = 2;
        n1.nexts.add(n2);
        n1.edges.add(new Edge(0, n1, n2));

        n2.out = 2;
        n2.in = 2;
        n2.nexts.add(n1);
        n2.edges.add(new Edge(0, n2, n1));

        List<Node> nodes = new ArrayList<>();
        nodes.add(n1);
        nodes.add(n2);

        List<Edge> edges = new ArrayList<>();
        edges.addAll(n1.edges);
        edges.addAll(n2.edges);

        Graph g = new Graph(nodes, edges);
        return g;
    }