算法练习(14)-二叉树中2个节点的最近公共祖先?
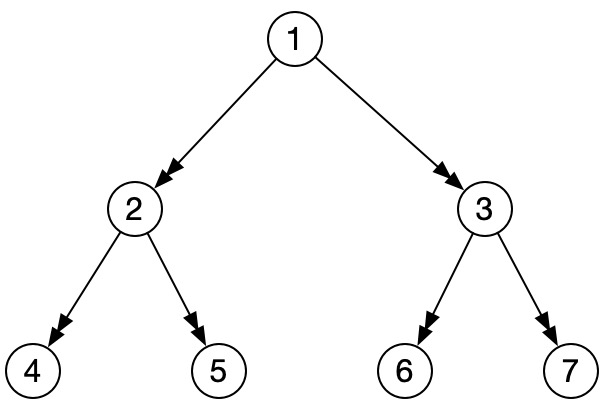
比如这颗树,给定2个节点: 4、5 ,它们的最近公共祖先节点为2。类似的,如果是3、5,它们的最近公共祖先节点为1。
一种比较容易想到的思路,如果知道每个节点到root的全路径, 比如
3到root节点的全路径为: 3->1
5到root节点的全路径为: 5->2->1
这样,只要遍历对比下全路径, 就能知道最近的公共节点是1,求每个节点到根节点全路径的方法,在以前的文章算法练习(11)-二叉树的各种遍历 有详细代码,此处直接复用即可。
/**
* 获取每个节点到根节点的全路径
*
* @param node
* @return
*/
public static Map<TreeNode, List<TreeNode>> getToRootPath(TreeNode node) {
if (node == null) {
return null;
}
//记录每个节点->父节点的1:1映射
Map<TreeNode, TreeNode> parentMap = new HashMap<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.add(node);
parentMap.put(node, null);
while (!queue.isEmpty()) {
TreeNode n = queue.poll();
if (n.left != null) {
queue.add(n.left);
parentMap.put(n.left, n);
}
if (n.right != null) {
queue.add(n.right);
parentMap.put(n.right, n);
}
}
//根据parentMap,整理出完整的到根节点的全路径
Map<TreeNode, List<TreeNode>> result = new HashMap<>();
for (Map.Entry<TreeNode, TreeNode> entry : parentMap.entrySet()) {
TreeNode self = entry.getKey();
TreeNode parent = entry.getValue();
//把当前节点,先保护起来
TreeNode temp = self;
List<TreeNode> path = new ArrayList<>();
while (parent != null) {
path.add(self);
self = parent;
parent = parentMap.get(self);
if (parent == null) {
path.add(self);
}
}
result.put(temp, path);
}
return result;
}
/**
* 求节点n1,n2的最近公共祖先
* @param root
* @param n1
* @param n2
* @return
*/
public static TreeNode getNearestSameParentNode(TreeNode root, TreeNode n1, TreeNode n2) {
if (n1 == null || n2 == null) {
return n1 == null ? n2 : n1;
}
if (n1.equals(n2)) {
return n1;
}
Map<TreeNode, List<TreeNode>> path = getToRootPath(root);
List<TreeNode> n1Path = path.get(n1);
List<TreeNode> n2Path = path.get(n2);
for (TreeNode node1 : n1Path) {
for (TreeNode node2 : n2Path) {
if (node1.equals(node2)) {
return node1;
}
}
}
return null;
}
public static void main(String[] args) {
TreeNode n1 = new TreeNode(1);
TreeNode n2_1 = new TreeNode(2);
TreeNode n2_2 = new TreeNode(3);
TreeNode n3_1 = new TreeNode(4);
TreeNode n3_2 = new TreeNode(5);
TreeNode n4_1 = new TreeNode(6);
TreeNode n4_2 = new TreeNode(7);
n1.left = n2_1;
n1.right = n2_2;
n2_1.left = n3_1;
n2_1.right = n3_2;
n2_2.left = n4_1;
n2_2.right = n4_2;
TreeNode result1 = getNearestSameParentNode(n1, n4_1, n4_2);
System.out.println(n4_1 + "/" + n4_2 + " : " + result1);
TreeNode result2 = getNearestSameParentNode(n1, n2_2, n3_2);
System.out.println(n2_2 + "/" + n3_2 + " : " + result2);
TreeNode result3 = getNearestSameParentNode(n1, n2_1, n3_1);
System.out.println(n2_1 + "/" + n3_1 + " : " + result3);
}
输出:
6/7 : 3 3/5 : 1 2/4 : 2
这个方法,虽然思路很容易理解 ,但效率并不高, 额外空间借助了2个Map,空间复杂度至少也是O(N)级别,然后再做2轮循环比较全路径,时间复杂度也可以优化,事实上有更好的解法:
public static TreeNode getNearestSameParentNode(TreeNode root, TreeNode n1, TreeNode n2) {
if (root == null || root == n1 || root == n2) {
return root;
}
TreeNode left = getNearestSameParentNode(root.left, n1, n2);
TreeNode right = getNearestSameParentNode(root.right, n1, n2);
if (left != null && right != null) {
return root;
}
return left != null ? left : right;
}
这个代码很短, 但不太好理解 , 先分析下一颗树中的2个节点X、Y,它们最近公共祖先的情况:
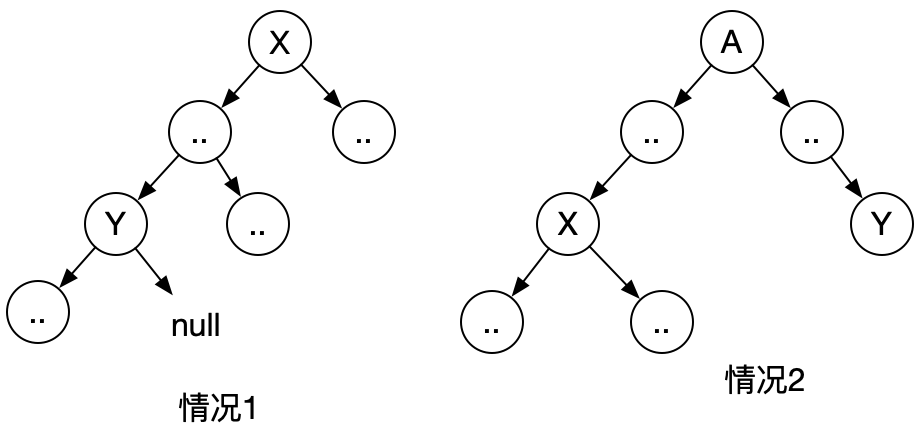
只会出现这2类情况:
1、节点X在Y的某1侧子树中(反过来也一样, Y出现在X的某1侧子树中),即:1个节点就是另1个的最近公共祖先。
2、节点X与Y,必须向上汇聚, 才能走到1个最近的交叉节点
在优化版的代码中,使用了递归求解。
第1段if判断,其实有2层意思,用于处理递归过程中的边界返回:
if (root == null || //递归到最末端叶节点时的函数返回
(root == n1 || root == n2) //在左右子树遍历过程中,如果发现当前节点就是n1或n2,直接返回,因为下面的子节点,肯定不可能再是它俩的公共祖先节点了
) {
return root;
}
最后1段return,表示遍历过程中,如果X或Y只出现在左子树中或右子树中,哪边出现就返回哪边,相当于下图这种情况,返回的是X,另1侧的返回null被扔掉.
return left != null ? left : right;
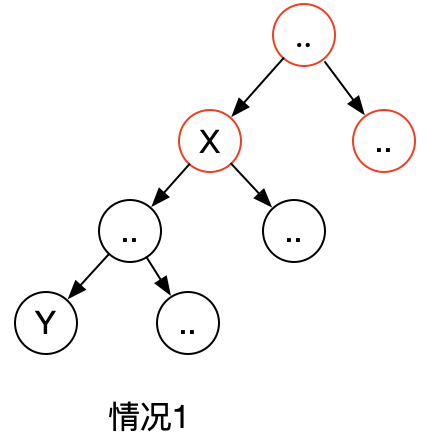
中间一段if,则表示是情况2:
if (left != null && right != null) {
return root;
}
在遍历的过程中,如果X与Y出现在某1个节点的2侧,最后左、右子树的遍历中, 会把它俩都返回过来,出现这种情况,说明X与Y汇聚于当前节点,这个节点就是最近的公共祖先。
作者:菩提树下的杨过
出处:http://yjmyzz.cnblogs.com
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。
出处:http://yjmyzz.cnblogs.com
本文版权归作者和博客园共有,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。


