链表（Java）实现
链表
先给出自定义的list接口，后面几种链表的实现了该接口
public interface List<E> {
//统计顺序表元素个数
int size();
//判断顺序表是否为空
boolean isEmpty();
//判断顺序表内是否有某个元素
boolean contains(Object o);
//向顺序表添加元素，添加成功放回true，向表尾添加
boolean add(E e);
//根据索引获取元素
E get(int index);
//根据索引设置元素
void set(int index, E value);
//根据索引移除元素
E remove(int index);
//向表头添加元素
void addFirst(E e);
//移除表头元素
E removeFirst();
//移除表尾元素
E removeLast();
}
单向链表的实现
public class SingleLinkedList<E> implements List<E> {
private int size = 0;
private Node<E> first;//链表头
private Node<E> last;//链表尾
public SingleLinkedList() {}
//内部类，对链表节点的抽象
private static class Node<E>{
E data;
Node<E> next;
public Node(E data) {
this.data = data;
}
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean contains(Object o) {
//引用类型为空
if(o == null) {
for (Node<E> x = first; x != null; x = x.next) {
if (x.data == null)
return true;
}
}
else{
//引用类型需要用equals()方法
for (Node<E> x = first; x != null; x = x.next) {
if (o.equals(x.data))
return true;
}
}
return false;
}
@Override
public boolean add(E e) {
final Node<E> l = last;//尾节点要指向新节点，先保存当前尾节点
final Node<E> node = new Node(e);
last = node;
//链表为空
if (!isEmpty())
first = node;//链表为空则新增节点成为首节点
else
l.next = node;//原尾节点指向新增节点
size ++;
return true;
}
private void CheckIndex(int index){
//当索引超出范围，抛出异常
if( index < 0 || index > size - 1 )
throw new IndexOutOfBoundsException("index " + index + " out of bounds");
}
@Override
public E get(int index) {
CheckIndex(index);
Node<E> x = first;
//遍历到索引位置
for (int i = 0; i < index; i++) {
x = x.next;
}
//返回数据
return x.data;
}
@Override
public void set(int index, E value) {
CheckIndex(index);
Node<E> x = first;
//遍历到索引位置
for (int i = 0; i < index; i++) {
x = x.next;
}
//修改数据
x.data = value;
}
@Override
public E remove(int index) {
CheckIndex(index);
Node<E> x;//待删除节点
Node<E> p = first;//删除节点的前一个
//待删除的是头节点
if (index == 0) {
x = first;
first = first.next;
} else {
//遍历到被删除节点的前一个
for (int i = 0; i < index - 1; i++) {
p = p.next;
}
x = p.next;//得到被删除节点
p.next = x.next;
}
size --;
return x.data;
}
@Override
public void addFirst(E e) {
Node<E> node = new Node<E>(e);
final Node<E> f = first;
first = node;
//链表为空，尾节点也要指向当前节点
if (size == 0) {
last = node;
} else {
node.next = f;
}
size ++;
}
@Override
public E removeFirst() {
return remove(0);
}
@Override
public E removeLast() {
return remove(size-1);
}
}
循环链表的实现
循环链表相比单向链表，有以下部分需要对原来的代码修改。
- contains()方法要设置退出机制
- add()方法，链表不为空时，新增节点的next要指向first
- remove()方法，要删除的是头节点，尾节点要指向新的first节点
public class SingleLinkedCircleList<E> implements List<E> {
private int size = 0;
private Node<E> first;//链表头
private Node<E> last;//链表尾
public SingleLinkedCircleList() {}
//内部类，对链表节点的抽象
private static class Node<E>{
E data;
Node<E> next;
public Node(E data) {
this.data = data;
}
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean contains(Object o) {
//引用类型为空
if(o == null) {
for (Node<E> x = first; x != null; x = x.next) {
if (x.data == null)
return true;
//设置退出机制：
if (x.next == first)
break;
}
} else {
for (Node<E> x = first; x != null; x = x.next) {
if (o.equals(x.data))
return true;
//设置退出机制：
if (x.next == first)
break;
}
}
return false;
}
@Override
public boolean add(E e) {
final Node<E> l = last;
final Node<E> node = new Node<E>(e);
last = node;
//链表为空
if(size == 0)
first = node;
else{
l.next = node;
node.next = first;
}
size ++;
return true;
}
private void CheckIndex(int index){
//当索引超出范围，抛出异常
if( index < 0 || index > size - 1 )
throw new IndexOutOfBoundsException("index " + index + " out of bounds");
}
@Override
public E get(int index) {
CheckIndex(index);
Node<E> x = first;
//遍历到索引位置
for (int i = 0; i < index; i++)
x = x.next;
//返回数据
return x.data;
}
@Override
public void set(int index, E value) {
CheckIndex(index);
Node<E> x = first;
//遍历到索引位置
for (int i = 0; i < index; i++)
x = x.next;
//修改数据
x.data = value;
}
@Override
public E remove(int index) {
CheckIndex(index);
Node<E> x;//待删除节点
Node<E> p = first;//删除节点的前一个
//待删除的是头节点，尾节点要指向新的头节点
if (index == 0) {
x = first;
first = first.next;
last.next = first;
}
else{
//遍历到被删除节点的前一个
for (int i = 0; i < index - 1; i++)
p = p.next;
x = p.next;//得到被删除节点
p.next = x.next;
}
size --;
return x.data;
}
@Override
public void addFirst(E e) {
Node<E> node = new Node<E>(e);
final Node<E> f = first;
first = node;
//链表为空，尾节点也要指向当前节点
if (size == 0) {
last = node;
} else {
node.next = f;
last.next = node;
}
size ++;
}
@Override
public E removeFirst() {
return remove(0);
}
@Override
public E removeLast() {
return remove(size - 1);
}
}
循环链表解决约瑟夫问题
N个人围成一圈，从第K个开始报数，第M个将被杀掉，最后剩下一个，其余人都将被杀掉。例如N=6，K=1，M=5，被杀掉的顺序是：5，4，6，2，3。
约瑟夫问题用链表求解非常简单，首先last和first先同时移动k-1步，然后进入循环，每前进m-1步就删除当前first指向的节点，删除用两句代码就可以实现：first = first.next; last.next = first 。
将约瑟夫问题解决方法也封装到了循环链表中。
public void JosephSolution(int num, int start, int m){
SingleLinkedCircleList<Integer> list = new SingleLinkedCircleList<Integer>();
//初始化约瑟夫环
for (int i = 0; i < num; i++)
list.add(i+1);
System.out.println("约瑟夫问题的出圈顺序");
//移动(start - 1)到起始位置
for (int i = 0; i < start - 1; i++) {
list.first = list.first.next;
list.last = list.last.next;
}
while(true){
if(list.first == list.last) {
System.out.println(list.first.data + "\n出圈结束");
break;
}
//每向下走(m-1)次到达需要删除的节点上。
for (int i = 0; i < m - 1; i++) {
list.last = list.last.next;
list.first = list.first.next;
}
System.out.printf(list.first.data + "->");
//以下两行是解决问题的关键所在，删除了当前first节点。first指向下一节点。
list.first = list.first.next;
list.last.next = list.first;
}
}
双向链表的实现
双向链表可以在任意节点向前向后遍历，查找效率高于单向链表。不过会占据更多存储空间。与单向链表相比，以下部分需要修改。
- add()方法，链表不为空时，新增节点的next要指向first。
- get()和set()方法，根据索引位置选择从头找还是从尾找。
- remove方法，从头开始找，删除头节点要特殊处理，其它情况时，被删除节点的下一节点的前驱指向p(此时p是被删除节点的前驱)；从尾开始找，删除为尾点节点要特殊处理，其它情况时，被删除节点的下一节点的后驱指向p(此时p是被删除节点的后驱)。从头从尾处理是对称的。
- addFirst()方法，链表不为空时，原来的首节点的前驱要指向当前新增加的节点。
public class LinkedList<E> implements List<E> {
private int size = 0;
private Node<E> first;//链表头
private Node<E> last;//链表尾
//内部类，对链表节点的抽象
public LinkedList() {}
private static class Node<E> {
E data;
Node<E> next;
Node<E> prev;
public Node(E data) {
this.data = data;
}
}
@Override
public int size() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public boolean contains(Object o) {
//引用类型为空
if(o == null) {
for (Node<E> x = first; x != null; x = x.next) {
if (x.data == null)
return true;
}
}
else{
//引用类型需要用equals()方法
for (Node<E> x = first; x != null; x = x.next) {
if (o.equals(x.data))
return true;
}
}
return false;
}
@Override
public boolean add(E e) {
final Node<E> node = new Node<E>(e);
final Node<E> l = last;
last = node;
//链表为空
if(isEmpty()){
first = node;
}else{
l.next = node;
node.prev = l;
}
size ++;
return true;
}
private void CheckIndex(int index){
//当索引超出范围，抛出异常
if( index < 0 || index > size - 1 )
throw new IndexOutOfBoundsException("index " + index + " out of bounds");
}
@Override
public E get(int index) {
CheckIndex(index);
Node<E> x;
//索引靠后，则从前往后遍历
if(index < (size >> 1)){
x = first;
for (int i = 0; i < index; i++)
x = x.next;
}
//索引靠后从后往前找
else{
x = last;
for (int i = 0; i < size - index - 1; i++)
x = x.prev;
}
return x.data;
}
@Override
public void set(int index, E value) {
Node<E> x;
CheckIndex(index);
if(index < (size >> 1)){
x = first;
for (int i = 0; i < index; i++)
x = x.next;
}
//索引靠后从后往前找
else{
x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
}
x.data = value;
}
@Override
public E remove(int index) {
CheckIndex(index);
final Node<E> x;//指向被删除节点
Node<E> p;//指向被删除节点的前驱节点或者后驱节点
//索引靠后，则从前往后遍历
if (index < (size >> 1)) {
//删除头指针，特殊处理
if (index == 0) {
x = first;
first = x.next;
} else {
p = first;//从前往后找被删除节点的前驱节点
for (int i = 0; i < index - 1; i++)
p = p.next;
x = p.next;//x指向被删除节点
p.next = x.next;
x.next.prev = p;//被删除节点的下一节点的前驱指向p
}
}
//索引靠后从后往前找
else {
//因为是从后往前找，删除尾节点也要同上面一样的方式处理
if (index == size - 1) {
x = last;
last = x.prev;
}else {
p = last;
for (int i = size - 1; i > index + 1; i--)
p = p.prev;//从后往前找删除节点的后驱节点
x = p.prev;
p.prev = x.prev;
x.prev.next = p;//被删除节点的下一节的后驱指向p
}
}
size --;
return x.data;
}
@Override
public void addFirst(E e) {
Node<E> node = new Node<E>(e);
final Node<E> f = first;
first = node;
//链表为空，尾节点也要指向当前节点
if (size == 0) {
last = node;
} else {
node.next = f;
f.prev = node;
}
size ++;
}
@Override
public E removeFirst() {
return remove(0);
}
@Override
public E removeLast() {
return remove(size - 1);
}
}
LeetCode链表练习题
206.Reverse Linked List(反转链表)
非递归方法:
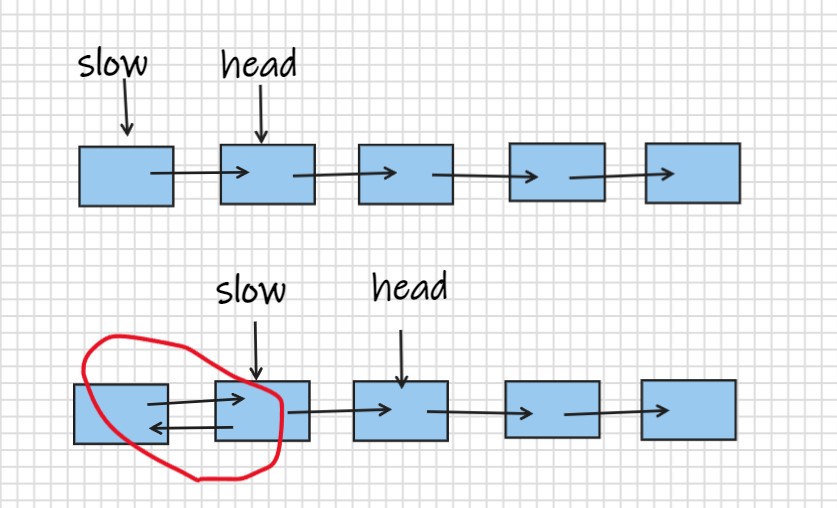
使用两个指针遍历链表(head和slow)，一个临时指针(temp)保存下一节点位置，这里要注意的问题是slow一开始要指向空，如果让slow指向head，head指向head.next，这种初状态转来遍历链表的话会出现环。
public ListNode reverseList(ListNode head) {
ListNode fast = head;
ListNode slow = null;
ListNode temp;
while(head != null){
temp = head.next;
head.next = slow;
slow = head;
head = temp;
}
return slow;
}
递归方法:
递归方法的思路是将head推到最后，然后在回溯的过程中，把节点的指向反转，同样要考虑形成环的可能。除此之外，写这道题意外的抛出了空指针异常，这是因为 if(head == null || head.next == null) 和 if(head.next == null || head == null) 是不一样的。如果链表为空，后一句先判断head.next == null，而head指向空没有next域，于是抛出空指针异常。
public ListNode reverseList(ListNode head) {
if(head == null || head.next == null)
return head;
ListNode res = reverseList(head.next);
head.next.next = head;
head.next = null;//没有这一行会出现环。
return res;
}
21.Merge Two Sorted List(合并两个有序链表)
非递归方法
一开始的思路是操作两个链表，然后插入另一个链表的节点，过程比较复杂，把自己给绕晕了。后来看了别人的解法，可以创建一个新的节点，然后只需要比较两个链表当前指向节点的数据大小，就可以让node的next指向它。如果一个链表为空，可以把另外一个链表后续的所有节点直接挂到next上
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
ListNode node = new ListNode();
ListNode dummy = node;
while(list1!=null && list2!=null){
if(list1.val <= list2.val){
node.next = list1;
list1 = list1.next;
}else{
node.next = list2;
list2 = list2.next;
}
node = node.next;
}
node.next = (list1==null)?list2:list1;
return dummy.next;
}
递归方法：
递归的解法很巧妙，没有多余空间的开销，而是只用两个链表就完成了操作，思路是分治法的思想：比较两个链表当前指向节点的数据域，小的那一个链表节点的next将指向以它下一个节点作为头节点的链表和和另外一个链表的合并。
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
if(list1==null)
return list2;
if(list2==null)
return list1;
if(list1.val < list2.val){
list1.next = mergeTwoLists(list1.next,list2);
return list1;
}else{
list2.next = mergeTwoLists(list1,list2.next);
return list2;
}
}
链表的实现参考《数据结构与算法基础（Java语言实现）》 作者：柳伟卫 北京大学出版社
