HDU 5416 CRB and Tree （2015多校第10场）

欢迎參加——每周六晚的BestCoder（有米！）

CRB and Tree

Time Limit: 8000/4000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)
Total Submission(s): 481    Accepted Submission(s): 151

Problem Description

CRB has a tree, whose vertices are labeled by 1, 2, …, . They are connected by  – 1 edges. Each edge has a weight.
For any two vertices  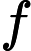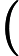and (possibly equal),  is xor(exclusive-or) sum of weights of all edges on the path from  to .
CRB’s task is for given 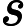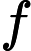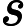, to calculate the number of unordered pairs  such that . Can you help him?

 

Input

There are multiple test cases. The first line of input contains an integer , indicating the number of test cases. For each test case:
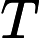The first line contains an integer  denoting the number of vertices.
Each of the next  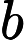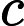- 1 lines contains three space separated integers ,  and  denoting an edge between  and , whose weight is .
The next line contains an integer 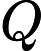 denoting the number of queries.
Each of the next  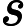lines contains a single integer .
1 ≤  ≤ 25
1 ≤  ≤ 
1 ≤  ≤ 10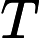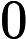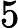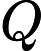
1 ≤ ,  ≤ 
0 ≤ ,  ≤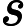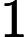 
It is guaranteed that given edges form a tree.

 

Output

For each query, output one line containing the answer.

 

Sample Input

1
3
1 2 1
2 3 2
3
2
3
4

 

Sample Output

1
1
0
Hint
For the first query, (2, 3) is the only pair that f(u, v) = 2.
For the second query, (1, 3) is the only one.
For the third query, there are no pair (u, v) such that f(u, v) = 4.
 

 

Author

KUT（DPRK）

解题思路：

由于异或是可逆的，因此从前到后记录前缀异或和，用hash表记录每一个值出现的次数，每次仅仅须要加上x ^ sum[v]出现的次数就可以。由于此时，u到v的异或和就是x。

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <stack>
#include <algorithm>
#define LL long long 
using namespace std;
const int MAXN = 100000 + 10;
struct Edge
{
	int to, next, w;
}edge[MAXN<<1];
int tot, head[MAXN];
int read()
{
	int res = 0, f = 1; char ch = getchar();
	while(ch < '0' || ch > '9'){if(ch == '-') f *= -1; ch = getchar();}
	while(ch >= '0' && ch <= '9'){res = res * 10 + ch - '0'; ch = getchar();}
	return res;
}
void init()
{
	tot = 0;
	memset(head, -1, sizeof(head));
}
void addedge(int u, int v, int w)
{
	edge[tot].to = v;
	edge[tot].w = w;
	edge[tot].next = head[u];
	head[u] = tot++;
}
int N, Q;
int vis[MAXN], st[MAXN<<2], op;
LL ans;
void dfs(int u, int x)
{
	vis[u] = 1; st[x]++;
	ans += st[op ^ x];
	for(int i=head[u];i!=-1;i=edge[i].next)
	{
		int v = edge[i].to, w = edge[i].w;
		if(!vis[v])
		{
			dfs(v, x ^ w);
		}
	}
}
int main()
{
	int T;
	scanf("%d", &T);
	while(T--)
	{
		N = read();
		int u, v, w;
		init();
		for(int i=1;i<N;i++)
		{
			u = read(); v = read(); w = read();
			addedge(u, v, w);
			addedge(v, u, w);
		}
		scanf("%d", &Q);
		while(Q--)
		{
			op = read();
			memset(vis, 0, sizeof(vis));
			memset(st, 0, sizeof(st));
			ans = 0;
			dfs(1, 0);
			printf("%I64d\n", ans);
		}
	}
	return 0;
}