笛卡尔树

性质

1. 其节点具有 \(2\) 个权值，分别是 \((key,val)\)，以 \(key\) 看，其为一颗二叉搜索树，以 \(val\) 看，其为一个堆（定义）。

• 二叉搜索树：左子树如果不空，则其权值一定小于根节点；右子树如果不空，则其权值一定大于根节点。

• 堆：完全二叉树，每个节点的值大于等于（或小于等于）其子树中的每个节点。

2. 如果笛卡尔树的 \((key,val)\) 键值确定，且 \(key,val\) 都分别互不相同，那么这个笛卡尔树的结构是唯一的。

3. 对于原正整数序列建树以后，区间 \([l,r]\) 的极值即是树上 \(l\) 所在位置以及 \(r\) 所在位置的 \(\text{LCA}\)。

4. 特殊的笛卡尔树：\(key\) 为数组下标，此时的笛卡尔树任意一个子树下标都是连续区间。

实现思路

将数组按照 \(key\) 排序，然后按序插入，显然我们每次只能将它插在最右边的末端。

对于每一个元素，我们从下往上比较最右边链上的所有点，如果找到一点 \(p\)，满足 \(p_{val}<u_{val}\) （大根堆就反过来），那么将 \(u\) 变为 \(p\) 的右儿子，而原右子树变为 \(u\) 的左子树。对于这条链，考虑用栈维护（每个点只会进栈出栈一次）。

时间复杂度 \(O(n)\)。

如下图：

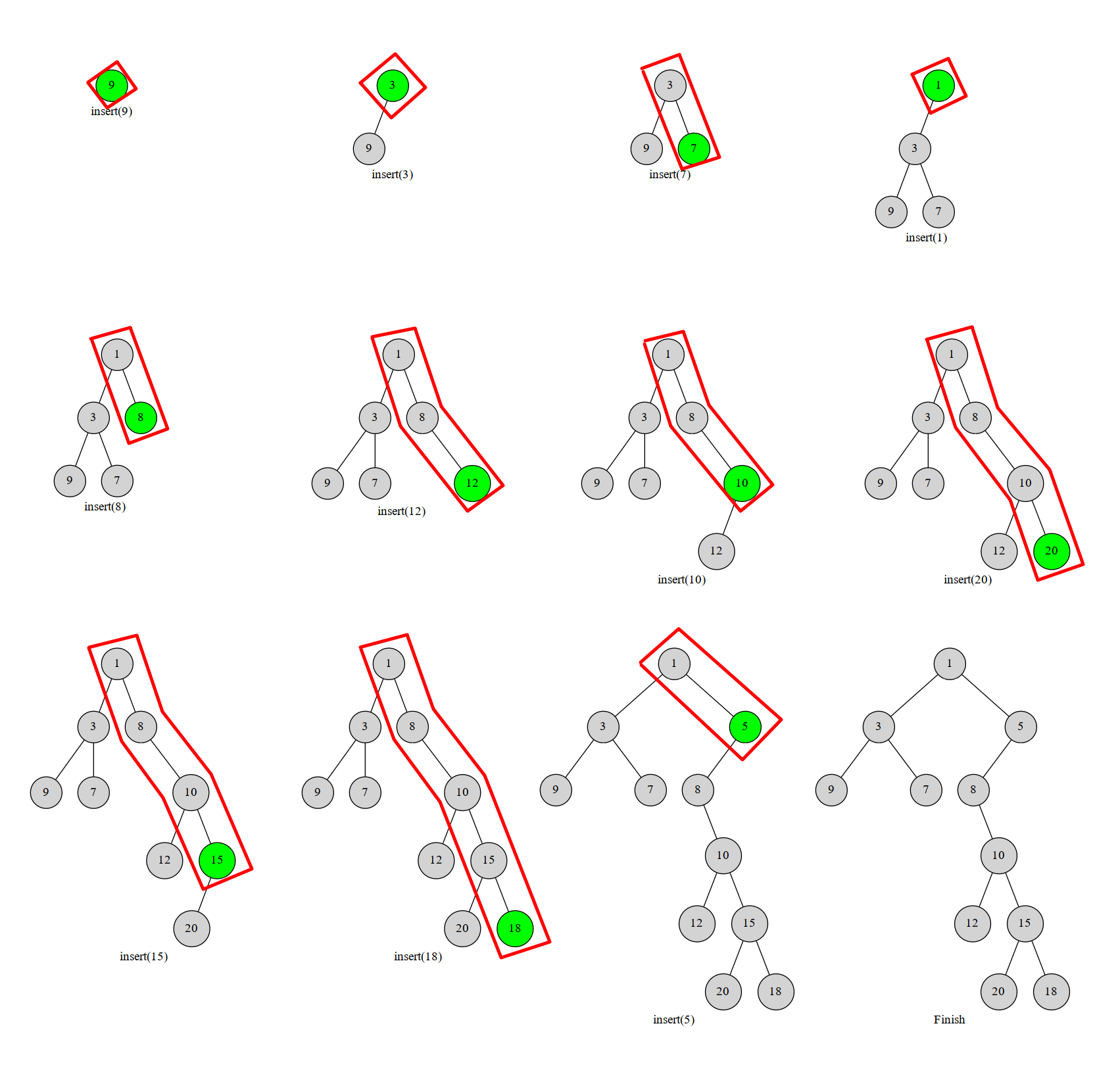
（图片来自 \(\text{oi-wiki}\)）

板子&习题

洛谷 P5854 【模板】笛卡尔树

#include<bits/stdc++.h>
#define int long long
#define debug puts("Shiina_Mashiro_kawaii")
#define ok puts("YES")
#define no puts("NO")
#define inf 1e9
using namespace std;
int read(){
	int x=0,f=1;char c=getchar();
	while(c<'0'||c>'9'){
		if(c=='-') f=-1;
		c=getchar();
	}
	while(c>='0'&&c<='9'){
		x=x*10+c-48;
		c=getchar();
	}
	return x*f;
}
const int maxn=1e7+5;
int n;
int ansl,ansr;
int a[maxn],l[maxn],r[maxn],tree[maxn];
void build_tree(){
	int top=0,dep=0;
	for(register int i=1;i<=n;++i){
		dep=top;
		while(a[i]<a[tree[dep]]){
			if(dep!=0) dep--;
		} //从下往上找
		if(dep<top) l[i]=tree[dep+1]; //将 u 变为 p 的右儿子
		if(dep!=0) r[tree[dep]]=i; //将原右子树变为 u 的左子树
        dep++;top=dep;
        tree[top]=i;
	}
}
inline void init(){
	n=read();
	for(register int i=1;i<=n;++i) a[i]=read();
	build_tree();
}
signed main(){
	init();
	for(register int i=1;i<=n;++i){
		ansl^=(l[i]+1)*i;ansr^=(r[i]+1)*i;
	}
    printf("%lld %lld",ansl,ansr);
}

附赠：练习题单