算法:HMM模型+维特比算法详解
一、HMM模型+维特比算法实例
1、问题描述
假设连续观察3天的海藻湿度为(Dry,Damp,Soggy),求这三天最可能的天气情况。
2、已知信息
①天气只有三类(Sunny,Cloudy,Rainy),海藻湿度有四类{Dry,Dryish, Damp,Soggy },而且海藻湿度和天气有一定的关系。
②隐藏的状态:Sunny, Cloudy, Rainy;
③观察状态序列:{Dry, Damp, Soggy}
④初始状态序列:
|
Sunny |
Cloudy |
Rainy |
|
0.63 |
0.17 |
0.20 |
⑤状态转移矩阵:
|
|
Sunny |
Cloudy |
Rainy |
|
Sunny |
0.5 |
0.375 |
0.125 |
|
Cloudy |
0.25 |
0.125 |
0.625 |
|
Rainy |
0.25 |
0.375 |
0.375 |
⑥发射矩阵:
|
|
Dry |
Dryish |
Damp |
Soggy |
|
Sunny |
0.6 |
0.2 |
0.15 |
0.05 |
|
Cloudy |
0.25 |
0.25 |
0.25 |
0.25 |
|
Rainy |
0.05 |
0.10 |
0.35 |
0.5 |
3、分析
由一阶HMM可知,Day2的天气仅取决于Day1;Day3的天气又只取决于Day2的天气。
4、计算过程
(1)Day1由于是初始状态,我们分别求
P(Day1-Sunny)=0.63*0.6;
P(Day1-Cloudy)=0.17*0.25;
P(Day1-Rain)=0.20*0.05;
Choose max{ P(Day1-Sunny) , P(Day1-Cloudy),P(Day1-Rainy)}, 得到P(Day1-Sunny)最大,得出第1天Sunny的概率最大。
(2)Day2的天气又取决于Day1的天气状况,同时也受Day2观察的海藻情况影响。
P(Day2-Sunny)= max{ P(Day1-Sunny)*0.5, P(Day1-Cloudy)*0.25, P(Day1-Rainy)*0.25} *0.15;
P(Day2-Cloudy)= max{ P(Day1-Sunny)*0.375, P(Day1-Cloudy)*0.125, P(Day1-Rainy)*0.625} *0.25;
P(Day2-Rainy)= max{ P(Day1-Sunny)*0.125, P(Day1-Cloudy)*0.625 , P(Day1-Rainy)*0.375} *0.35;
Choosemax{ P(Day2-Sunny) , P(Day2-Cloudy), P(Day2-Rainy)},得到P(Day2-Cloudy)最大,得出第2天Cloudy的概率最大。
故{Sunny,Cloudy}是前两天最大可能的天气序列。
(3)Day3的天气又取决于Day2的天气状况,同时也受Day3观察的海藻情况影响。
P(Day3-Sunny)= max{ P(Day2-Sunny)*0.5, P(Day2-Cloudy)*0.25, P(Day2-Rainy)*0.25} *0.05;
P(Day3-Cloudy)= max{ P(Day2-Sunny)*0.375, P(Day2-Cloudy)*0.125, P(Day2-Rainy)*0.625} *0.25;
P(Day3-Rainy)= max{ P(Day2-Sunny)*0.125, P(Day2-Cloudy)*0.625, P(Day2-Rainy)*0.375} *0. 05;
Choosemax{ P(Day3-Sunny) , P(Day3-Cloudy), P(Day3-Rainy)},得到P(Day3-Rainy)最大,得出第3天Rainy的概率最大。故{Sunny,Cloudy,Rainy}是这三天最可能的天气序列。
5.Python代码
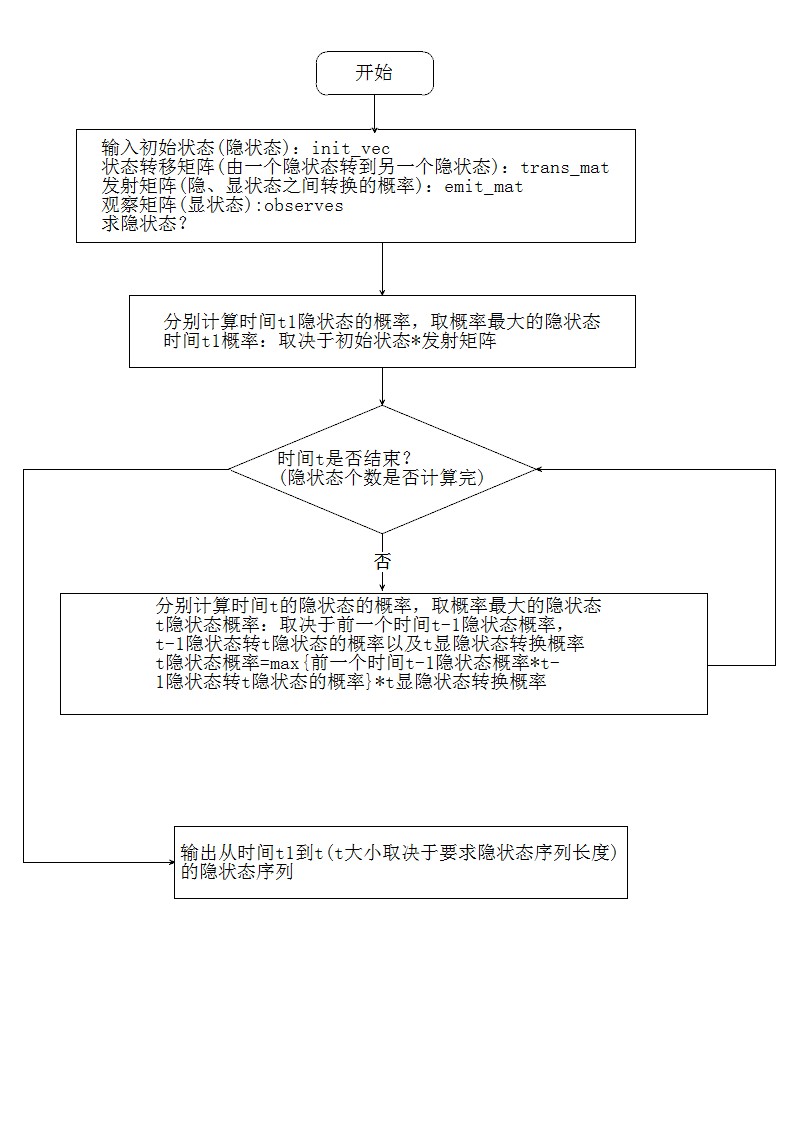
流程图:

1 #-*- coding:utf-8 -*- 2 __author__ = 'Administrator' 3 4 init_vec={"sunny":0.63,"cloudy":0.17,"rainy":0.20} 5 trans_mat={"sunny":{"sunny":0.5,"cloudy":0.375,"rainy":0.125}, 6 "cloudy":{"sunny":0.25,"cloudy":0.125,"rainy":0.625}, 7 "rainy":{"sunny":0.25,"cloudy":0.375,"rainy":0.375}} 8 emit_mat={"sunny":{"dry":0.6,"dryish":0.2,"damp":0.15,"soggy":0.05}, 9 "cloudy":{"dry":0.25,"dryish":0.25,"damp":0.25,"soggy":0.25}, 10 "rainy":{"dry":0.05,"dryish":0.10,"damp":0.35,"soggy":0.50}} 11 observes=["dry","damp","soggy"] 12 states=["sunny","cloudy","rainy"] 13 14 #列表中包含字典,就相当于二阶列表使用 15 tab=[{}] #只有一行 16 path=[{}] 17 for t in range(len(observes)): 18 #print(t) 19 if t==0: 20 temp=[] 21 for state in states: 22 prob=init_vec[state]*emit_mat[state].get(observes[t]) 23 tab[0][state]=prob 24 temp.append((prob,state)) 25 best_prob,best_state=max(temp,key=lambda x:x[0]) 26 path[0][best_state]=best_prob 27 else: 28 tab.append({}) 29 path.append({}) 30 temp=[] 31 for state1 in states: 32 item=[] 33 for state2 in states: 34 prob=tab[t-1][state2]*trans_mat[state2].get(state1)*emit_mat[state1].get(observes[t]) 35 item.append((prob,state2)) 36 best_prob,best_state=max(item,key=lambda x:x[0]) 37 tab[t][state1]=best_prob 38 temp.append((best_prob,state1)) 39 best_prob,best_state=max(temp,key=lambda x:x[0]) 40 path[t][best_state]=best_prob 41 print(tab) 42 print(path)
输出结果:
[{'rainy': 0.010000000000000002, 'cloudy': 0.0425, 'sunny': 0.378}, {'rainy': 0.0165375, 'cloudy': 0.0354375, 'sunny': 0.02835}, {'rainy': 0.01107421875, 'cloudy': 0.0026578125, 'sunny': 0.0007087500000000001}]
[{'sunny': 0.378}, {'cloudy': 0.0354375}, {'rainy': 0.01107421875}]



