并查集

并查集

引入：

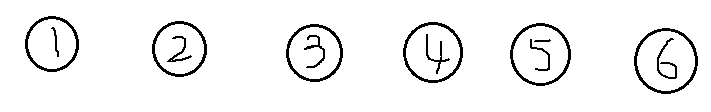
有6个小球。

命令

　　1、把1和2所在的集合合并。

　　2、把2和3所在的集合合并。

　　3、把3和4所在的集合合并。

　　……

　　5、   把5和6所在的集合合并。

　　按照以前的想法，可能会更改下标，把1的下标改为2。

执行命令1、

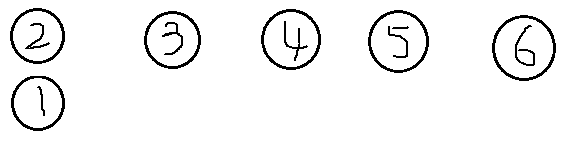
2、

......

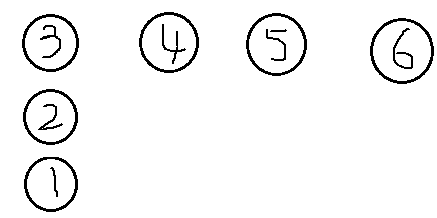
5、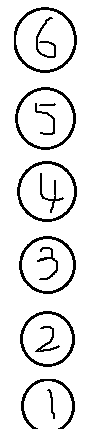

　　这样虽然能够达到目的，但是，时间复杂度为o（n），每一次把小球拿出来，又放进去……

 

　　我们又想，那能不能把个数小集合的合并到个数大的集合那边呢。

 

　　这叫做启发式排序：把小的拿到大的。虽然看上去好像也没省多少时间…(⊙_⊙;) 但事实上，省了很多时间，时间复杂度变成了n log n。（⊙o⊙）目瞪口呆

 

　　不过呢，这还不是最省时间的方案哦，老大登场：并查集。[铛铛铛]

 

　　其实所谓的并查集，就是找祖宗ancestor，一路深搜下去，看自己的祖先是谁，当然，祖先的祖先就是自己啦。再返回。

 

　　虽然每一次都一路深搜下去，会很慢，所以就要用到“路径压缩”，在退回来的同时，把自己的根节点变为祖先。这样子就省了“前辈”的时间啦。

但是，别忘了一开始所有节点的祖先都是自己。