webgl笔记-4.光照原理和光照渲染

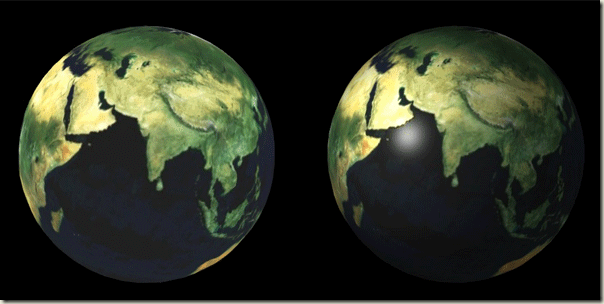
黑暗中无法看到不发光的物体。不考虑光照的webgl程序为立方体的每个三角形平面的每个顶点指定了颜色，这些颜色值被线形内插到该平面投影到屏幕的每个像素上，这实际上是将物体当作光源来处理，指定顶点的颜色其实就是指定了物体表面发光的颜色。显然，实际上大部分物体都不是光源，它们具有颜色是因为这些物体的表面对可见光的反射具有选择性。光照能够在极大的程度上增加场景的逼真度，下面是一个地球仪场景的开启光照前后的表现。
在开启光照前，地球仪很诡异地像一个发着荧光的物体，而开启光照后，地球仪逼真了很多。这张图片中对地球仪使用了环境光、可以指定方向的平行光、可以指定位置的点光源光、还开启了高光反射（不严格的镜面反射）。这些不同模式的光照原理将在这篇博文中作简单的记录。

 

从webgl的角度说，实现光照的具体工作就是：按照光照的物理机制针对性地更新每个像素的颜色值，该像素颜色的新值计算一定由光照的性质和物体表面颜色两种因素影响。物体表面的颜色——不管是纯色、渐变色或是纹理，其物理意义已经由光源色变成了对光的反射率。

环境光

环境光，一般是指由于其他物体表面漫反射、空气中的微粒散射产生的光。环境光在所有方向上颜色和强度一样。假定某一个像素，其对光照的反射率为S（三维向量，表示对红、绿、蓝的反射率），环境光的颜色是L，最终该像素点在屏幕上呈现的颜色C应该是：

$$C=\begin{bmatrix}C_{R}\\ C_{G}\\ C_{B}\end{bmatrix}=\begin{bmatrix}L_{R}\times S_{R}\\ L_{G}\times S_{G}\\ L_{B}\times S_{B}\end{bmatrix}$$

一般来说，环境光是灰度色，三个分量L（R，G，B）是相等的。但如果环境光的R分量较高，比如（0.8，0.5，0.5），说明环境光是红色的（想象在一座窗户玻璃是红色的房间里），最后得到的颜色值也是偏红色的，如果有一个青色的物体，反射率为（0.5，0.8，0.8），那么最后看上去是将是……灰色的。

环境光对颜色的影响很直接，但是其他种类的光则不一样：光照对像素的影响可能和像素或顶点位置、光照方向等有关。但是我们先将不考虑那些，模仿环境光模式将光照对颜色的影响定义为一个影响因子F，这样任何光照情况都遵循以下的规律，而我们只需要考虑具体不同光照情况下F的变化。

$$C=\begin{bmatrix}C_{R}\\ C_{G}\\ C_{B}\end{bmatrix}=\begin{bmatrix}F_{R}\times S_{R}\\ F_{G}\times S_{G}\\ F_{B}\times S_{B}\end{bmatrix}$$

对于环境光，很简单的是：

$$F=\begin{bmatrix}F_{R}\\ F_{G}\\ F_{B}\end{bmatrix}=\begin{bmatrix}L_{R}\\ L_{G}\\ L_{B}\end{bmatrix}$$

光照处理在着色器中进行，处理环境光的代码如下：

<!-- 片元着色器 --> 
<script id="shader-fs" type="x-shader/x-fragment"> 
……  
varying vec3 vAmbientLightWeighting; 
    void main(void) { 
        vec4 noLightColor; // 计算不受光照影响（或者说受到标准光照）时的颜色 

        …… 
        gl_FragColor = vec4(noLightColor.rgb * vAmbientLightWeighting, noLightColor.a); 
    } 
</script>
<!-- 顶点着色器 –> 
<script id="shader-vs" type="x-shader/x-vertex">  
    …… 
    uniform vec3 uAmbientColor;  
    varying vec3 vAmbientLightWeighting;  
    void main(void) { 
        …… 
        vAmbientLightWeighting = uAmbientColor; 
    } 
</script>

环境光不受顶点位置影响，传入表示环境光颜色的uniform变量，顶点着色器中将每个顶点收到光照的影响因子计算（对于环境光就是直接赋值）出来，交给片元着色器处理颜色。

平行光

当光源距离物体足够远的时候，光线可以视作平行光，最典型的例子就是日光。平行光具有方向，其照射到物体表面的角度影响了表面对光的反射。在这一节仅仅考虑物体表面发生的漫反射——各方向无差别地反射光线。

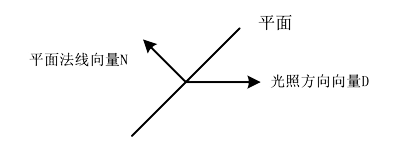
显然的事情是，入射光垂直照射到表面上会使反射光最强，入射角越大，反射光强度越小。因此平行光的光照影响因子与光照方向和平面的法线方向有关，同时注意到光照方向的背面是没有光照的，因此光照方向和平面法线夹角在90度以内时，光照影响因子为0向量。综上，光照因子为：

$$F=\begin{bmatrix}F_{R}\\ F_{G}\\ F_{B}\end{bmatrix}=\begin{bmatrix}L_{R}\\ L_{G}\\ L_{B}\end{bmatrix}\cdot max\{-\cos\theta,0\}$$

夹角余弦值由归一化的光照向量和法线向量点乘得到

$$\cos\theta=\frac{D}{|D|}\cdot\frac{N}{|N|}$$

平行光的方向和颜色与顶点无关，但是平行光对于像元颜色的影响因子F却严重依赖于物体的位置和状态。上述计算影响因子的过程在着色器中进行，在此之前需要传入表示平行光方向和颜色的uniform变量，还要组织一个缓冲区，对应于每个顶点（所属平面）的法线向量。

片元着色器的代码与环境光相同，不同的是顶点着色器中计算varying变量vLightWeighting的过程。

<!-- 顶点着色器 –> 
<script id="shader-vs" type="x-shader/x-vertex"> 
    …… 
    attribute vec3 aVertexNormal; // 法线  
    uniform mat3 uNMatrix; // 模型矩阵3阶子矩阵的逆转置矩阵 
    uniform vec3 uLightingDirection; // 平行光方向 
    uniform vec3 uDirectionalColor; // 平行光颜色 
    varying vec3 vLightWeighting; // 光照影响因子 
    void main(void) { 
        ……  
        vec3 transformedNormal = uNMatrix * aVertexNormal; 
        float directionalLightWeighting = max(dot(transformedNormal, uLightingDirection), 0.0); 
        vLightWeighting = vLightWeighting + uDirectionalColor * directionalLightWeighting; 
     } 
</script>

物体运动时，法线也会变化，处理法线运动的一个好方法是使用齐次坐标：

齐次坐标中向量的第四个分量是0，而点坐标第四个分量是1，将模型矩阵乘以法线向量就能得到变换后的法线向量，但是这样不能保证法线向量的模仍然为1，你也许要再次归一化法线向量。Learning WebGL的代码中应用的方法是将模型矩阵中取左上角3阶子矩阵，并作逆转置，得到的矩阵仅保留了模型矩阵中的正交部分，即旋转变换造成的影响。也许这样做代码的效率更高吧。

点光源

点光源和平行光的不同在于，对每一个顶点，法线向量和光照方向向量都是变化的。和平行光处理过程类似，仅在这里有差异：

$$\cos\theta=\frac{D}{|D|}\cdot\frac{N}{|N|}$$

在平行光处理中，向量D是一个直接的常量，而在点光源处理中，D需要用正在处理的顶点坐标减去光源坐标才可以。在着色器中，将代表平行光方向的常量替换为代表点光源位置的常量，并按照点光源的机制计算光照影响因子。

<!-- 顶点着色器 –> 
<script id="shader-vs" type="x-shader/x-vertex"> 
    …… 
    attribute vec3 aVertexNormal;  
    uniform mat3 uNMatrix;  
    uniform vec3 uPointLightingLocation; 
    uniform vec3 uPointLightingColor;  
    varying vec3 vLightWeighting;  
    void main(void) { 
        …… 
        vec3 lightDirection = normalize(uPointLightingLocation - mvPosition.xyz);  
        vec3 transformedNormal = uNMatrix * aVertexNormal; 
        float directionalLightWeighting = max(dot(transformedNormal, lightDirection), 0.0); 
        vLightWeighting = vLightWeighting + uPointLightingColor * directionalLightWeighting; 
    } 
</script>

注意到光照方向需要归一化：在平行光那一节中这个工作由javascript完成，这里由着色器完成。

逐像元光照

上面提到的三种光照模式都遵循这样的规律：对每个顶点给出光照影响因子vLightWeighting，该因子在图元光栅化过程中线形内插到对应于每个片元，在片元着色器中使用内插后的光照影响因子“修正”物体本身的颜色值（虽然逻辑上应该是后者“修正”前者，因为先有光，才谈得上反射，但这里跟没有光照时的“物体即光源”模式相比，也就这样说吧）。这种光照渲染模式称为逐顶点光照——光照逻辑止于对顶点的处理。一个简单的例子能够说明逐像元光照的缺点。

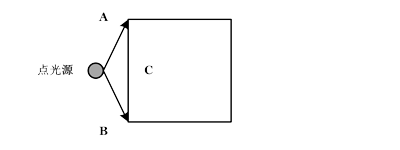
假设点光源很靠近立方体的某个表面，如图所示，整个表面应该被照亮了。按照实际情况，C点处应当最亮，A点和B点较为晦暗。但是采用逐顶点光照法渲染场景时，着色器对A和B计算光照影响因子（较低），然后线形内插到整个表面（包括C点），这样C点的光照影响因子也会较低，因此显示不出C点较A、B两点明亮的实际情况。

逐像元光照的具体思路是：将光线方向向量和法线向量全部线形内插到对应于单个片元，然后在片元着色器中计算影响因子。

<!-- 片元着色器 –> 
<script id="per-fragment-lighting-fs" type="x-shader/x-fragment"> 
    ……  
    varying vec3 vTransformedNormal; 
    varying vec4 vPosition;  
    uniform vec3 uPointLightingLocation; 
    uniform vec3 uPointLightingColor;  
    void main(void) { 
        vec3 lightWeighting; // 逐片元的光照影响因子 
        vec3 lightDirection = normalize(uPointLightingLocation - vPosition.xyz); // 光照方向模1向量 
        float directionalLightWeighting = max(dot(normalize(vTransformedNormal), lightDirection), 0.0); 
        lightWeighting = lightWeighting + uPointLightingColor * directionalLightWeighting; 
        ……  
    } 
</script>

<!-- 顶点着色器 –> 
<script id="per-fragment-lighting-vs" type="x-shader/x-vertex">  
    …… 
    varying vec2 vTextureCoord; 
    varying vec3 vTransformedNormal; 
    varying vec4 vPosition;  
    void main(void) { 
        vPosition = uMVMatrix * vec4(aVertexPosition, 1.0); // 传递顶点空间位置 
        …… 
        vTransformedNormal = uNMatrix * aVertexNormal; // 传递法线向量 
    } 
</script>

大部分情况下，一个平面上的数个顶点的法线向量是一致的，但是用大量平面模拟曲面的时候，同一平面上顶点的法线向量不一致却能取得更好的渲染效果——因为在被模拟的那个“真实”的曲面上，那些点位置的法线向量就不一样。因此上述顶点着色器中讲法线向量传递给图元光栅化是有意义的。

光泽：镜面反射

很多情况下需要采用镜面反射，严格的镜面反射定律：入射角等于反射角。现实中有光泽的物体表面实际上遵循着一种介于镜面反射和漫反射之间的规律。

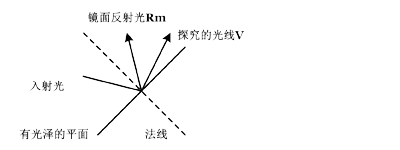
如图，V为相机接收的光线，其颜色正是需要用来指定屏幕上该像素的颜色。V方向光照的强度为镜面反射光Rm向量和相机接受光线V向量点乘的a次幂。a是关于物体表面性质的描述常量。

$$F=(R_{m}\cdot V)^{\alpha}$$

镜面反射的片元着色器代码中最重要的若干行：

// 获取归一化相机接受光线V的方向向量 
vec3 eyeDirection = normalize(-vPosition.xyz); 
// 根据光照方向和法线方向计算严格镜面反射光Rm的方向向量 
vec3 reflectionDirection = reflect(-lightDirection, normal); 
// 计算镜面反射光影响因子，uMaterialShininess为常量指数a 
specularLightWeighting = pow(max(dot(reflectionDirection, eyeDirection), 0.0), uMaterialShininess);

其他

这篇博文算是一篇笔记，总结了图形学中的几种常用光照模式原理及其在webgl中的实现，如果你也在学习这些知识，希望对你有所帮助。
本篇博文中的代码全部来自HiWebGL站点翻译的WebGL教程，对代码的解释是我自己的理解。因为我也是初学WebGL，所以我的理解几乎一定会有错误，如果你发现了，恳请你指出。