博客作业06--图
1.学习总结(2分)
1.1图的思维导图
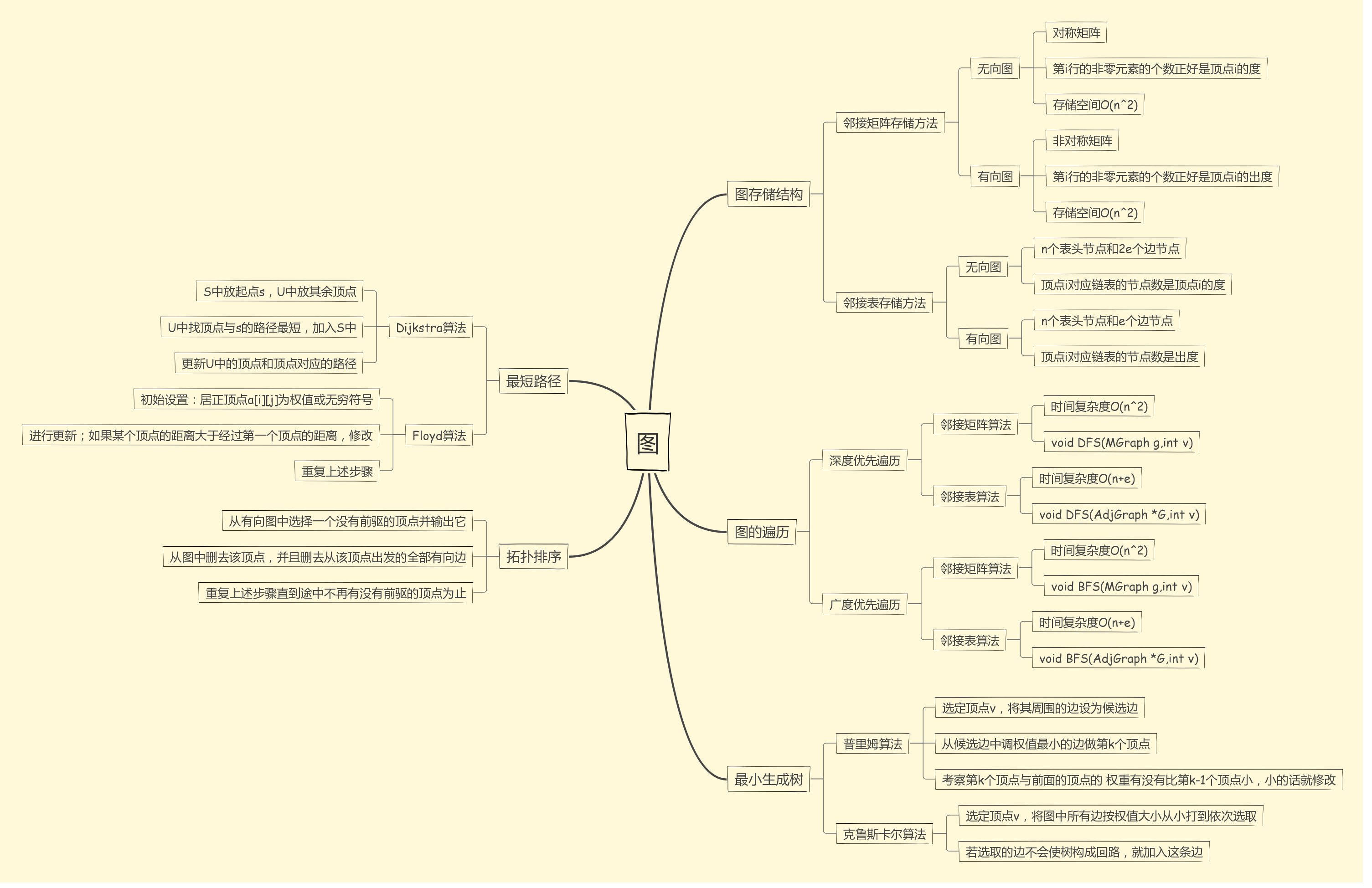
1.2 图结构学习体会
深度遍历算法
深度遍历就是访问一个点的一个相邻点,通过递归的方法使得从某个顶点出发遍历全部的顶点。
广度遍历算法
广度遍历是访问一个点的全部相邻点,用队列记录所访问的每个点的顺序。
Prim和Kruscal算法
普里姆算法是遍历某个顶点的所有相邻点,找出权值最小的边做需要的边,直到连接好所有的顶点;
Dijkstra算法
拓扑排序算法
拓扑排序就是寻找和输出没有前驱的顶点,如果遇到环路说明无法构成拓扑排序
2.PTA实验作业(4分)
2.1 题目1:7-2 排座位
2.2 设计思路(伪代码或流程图)
1.构建图结构体,定义全局变量visited[]用来标记是否遍历
2.建邻接矩阵的图,输入它们之间的关系(-1 0 1 三种情况);
3.for(i=0 to count){
输入顶点k1,k2;
如果关系为1,是朋友;
如果关系为0,不是朋友也不是敌人;
如果关系为-1,{
广度遍历有没有共同朋友;
有的话输出“OK, but。。。”
没有的话是敌人;
}
4.return 0;
2.3 代码截图
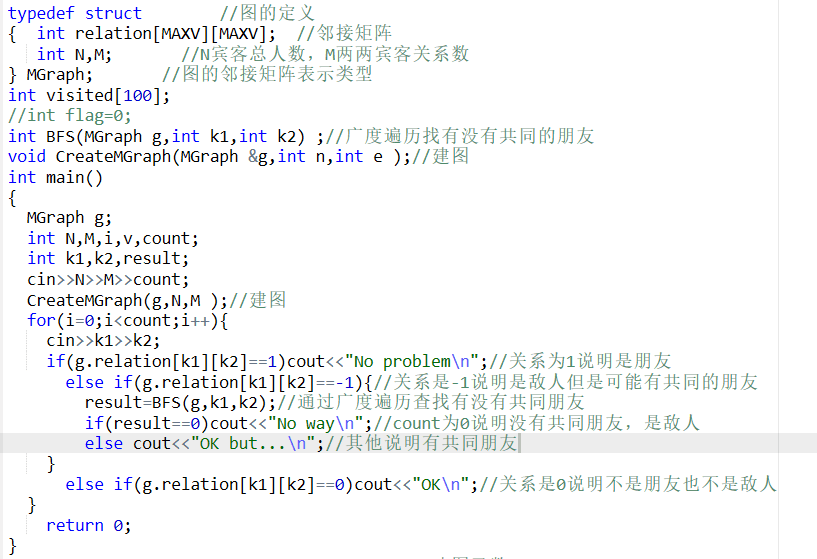

2.4 PTA提交列表说明。
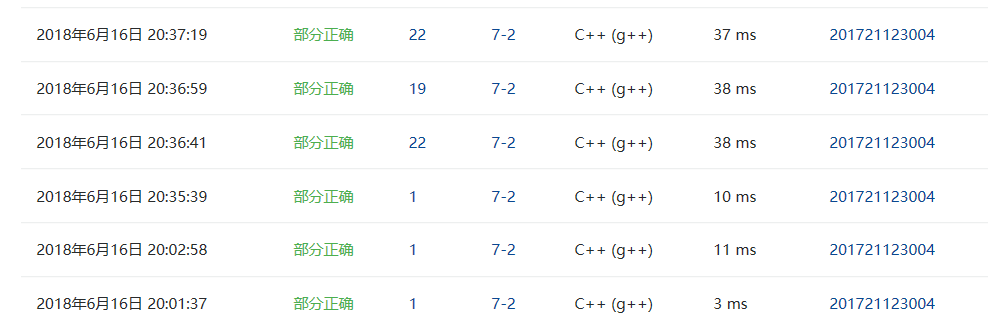
这道题只有得一分得问题是我对MAXV的长度定为了20,改为了101后分数就升到了22分,但是还差的三分错误是 ( 最大N,全连通环,全查询),没能改出来这个错误。
2.1 题目1:7-4 公路村村通
2.2 设计思路(伪代码或流程图)
1.定义各个全局变量,如代码截图;其中visited[]数组记录所有顶点是否都被遍历;
2.输入顶点数n,和边树e;
3.入宫边数小于顶点数,输出-1;
4.建邻接矩阵图,填入权值;
5.普里姆函数找最小生成树;
6.如果visited[]数组中有未被遍历的点,输出-1;否则输出flag,即最低成本;
7.普里姆函数 prim(int v){
定义lowcost[]和closest[]数组以及min存放实时最小成本;
给两个数组赋初值 lowcost[i]=edges[v][i];closest[i]=v;
for (i=0 to n){
min定初值无穷大;
for(j=1 to n)如果lowcost数组不为0且小于min,min值更新,k=j;
最低成本flag=flag+1;
两个数组重新赋值0和1;
修改数组的值 lowcost[j]=edges[k][j];closest[j]=k;
}
2.3 代码截图

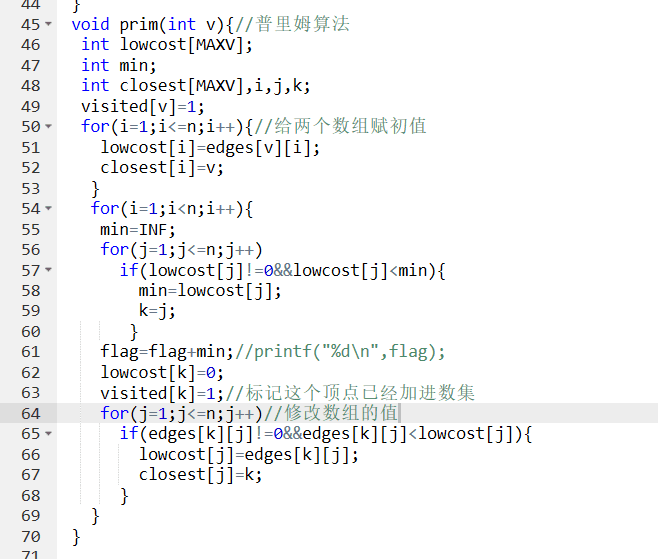
2.4 PTA提交列表说明。


从十五分到25分之间有两个错误,一个和上一题一样是数组长度没有改成题目要求的1000,还有一个是当边数小于顶点数的时候没有输出-1;还差的最后一个错误依然是(最大N和M,连通)这个错误,没有改出来。
2.1 题目1:7-7 旅游规划
2.2 设计思路
1。定义各个全局变量数组,模仿邻接矩阵的数组形式
2.给路径数组和开销数组赋初值为501;
3.根据输入修改路径数组和开销数组的值;
4.用两个新的数组记录S出发城市下的到每个城市的路径长度和开销;
5.Dijkstra算法求最小路径长度和开销;
6.输出路径长度和开销;
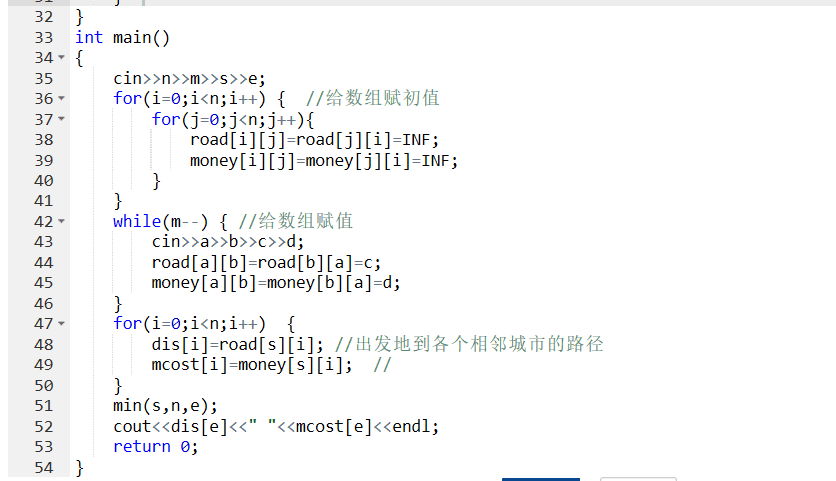
2.3 代码截图

2.4 PTA提交列表说明。


3.截图本周题目集的PTA最后排名(3分)
本次题目集总分:310分
3.1 PTA排名

3.2 我的总分:
2分
4. 阅读代码(必做,1分)
#include <stdio.h>
#include<stdlib.h>
#define FULL 250001
typedef struct node *Node;
typedef struct {
int Node;//目标结点
int Lenth;//边长
} data;
struct node {
data Reached[501];//与之有边连接的结点集合
int right;//集合里的结点个数
};
int teams[501];//保存每个结点带有的救援队数目
int Lenth[501][3];//[0]记录从起点出发到各结点的路径长度 ;[1]记录该路径能获取的救援队总数;【2】记录等长路径条数
Node Map;//地图
int cmp(const void*a,const void*b) {//
data*x=(data*)a;
data*y=(data*)b;
if(x->Lenth!=y->Lenth) {
return x->Lenth-y->Lenth;
} else if(teams[x->Node]!=teams[y->Node]) {
return teams[y->Node]-teams[x->Node];
} else return teams[x->Node]-teams[y->Node];
}
void Dijkstra(int);
void DFS(int,const int);
int main() {
int N,M,S,D;//结点数、边数、起点、终点
scanf("%d%d%d%d",&N,&M,&S,&D);
Map=(Node)malloc(sizeof(struct node)*N);//初始化地图上的结点
for(int i=0; i<N; Map[i++].right=0);
for(int i=0; i<N; scanf("%d",&teams[i++]));//读入每个结点的价值——城市拥有的救援队数量
{
//读入地图信息,并排序整理
while(M--) {
int a,b,lenth;
scanf("%d%d%d",&a,&b,&lenth);
Map[a].Reached[Map[a].right].Node=b;
Map[a].Reached[Map[a].right++].Lenth=lenth;
Map[b].Reached[Map[b].right].Node=a;
Map[b].Reached[Map[b].right++].Lenth =lenth;
}
for(int i=0; i<N; i++) {
// printf("\n%d:",i);
qsort(Map[i].Reached,Map[i].right,sizeof(data),cmp);
for(int j=0; j<Map[i].right; j++) {
// printf("{%d-%d}",Map[i].Reached[j].Node,Map[i].Reached[j].Lenth);
}
}
}
for(int i=0; i<N; Lenth[i++][0]=FULL); //[0]初始化设定从起点到所有其他结点的路径长度为无穷;
Lenth[S][0]=0;
Lenth[S][1]=teams[S];
Dijkstra(S);
printf("%d %d\n",Lenth[D][2],Lenth[D][1]);
DFS(D,S);
printf("%d",D);
return 0;
}
void Dijkstra(int a) {//戴克斯特拉算法
for(int i=0; i<Map[a].right; i++) {
data temp=Map[a].Reached[i];
if(Lenth[a][0]+temp.Lenth<Lenth[temp.Node][0]) {
Lenth[temp.Node][0]=Lenth[a][0]+temp.Lenth;
Lenth[temp.Node][1]=Lenth[a][1]+teams[temp.Node];
Lenth[temp.Node][2]=1;
Dijkstra(temp.Node);
} else if(Lenth[a][0]+temp.Lenth==Lenth[temp.Node][0]) {
if(Lenth[a][1]+teams[temp.Node]>Lenth[temp.Node][1]) {
Lenth[temp.Node][1]=Lenth[a][1]+teams[temp.Node];
}
++Lenth[temp.Node][2];
Dijkstra(temp.Node);
}
}
}
void DFS(int dd,const int S) {//深度优先,从终点递归回溯, 如果存在某个结点:它到终点的边长加上它到起点的长度== 终点到原点的长度&&它到起点的救援队数量+终点的救援队数量== 起点到终点的救援队数量,那么这个结点一定是最短路上的一个结点。
if(dd==S)return;
for(int i=0; i<Map[dd].right; i++) {
data temp=Map[dd].Reached[i];
if(Lenth[temp.Node][0]+temp.Lenth==Lenth[dd][0]&&
Lenth[temp.Node][1]+teams[dd]==Lenth[dd][1]) {
// printf("*");
DFS(temp.Node,S);
printf("%d ",temp.Node);
}
}
}



