四叉树平面分割算法--快速图元搜索
环境：Visual Studio 2017 + .Net Framework 4.5 + C#
用途：在二维平面上快速定位某个点有哪些图元。
算法说明：
1，平面分割
本文使用完全四叉树算法（除了叶节点之外，每个节点都包含四个子节点），对平面进行分割。
每添加一个图元，判断当前象限（本文把每个节点称之为象限/Quadrant，根节点，即整个画布也是一个象限）中的图元个数，
如果当前象限中的图元超出某个阈值（假设，每个象限最多包含四个图元），则对象限进行分割（分割为四个子象限）。
然后，把当前象限中的图元放到子象限中（把图元数据从当前象限移到子象限中）。假如，子象限的Rectangle不足以包含整个
图元，则不移动。
2，图元搜索
给定一个点（Point），从根节点开始搜索，判断根节点中的图元（的Rectangle）是否包含给定的点（Point）。如果包含，则
把整个图元添加到结果集中，否则判断四个子象限（四个子节点）是否包含给定的点（Point），再判断其内部的图元是否包含
这个点。重复此过程，直至象限没有子象限。
下面展示一下四叉树搜索和线性表搜索算法时间效率的对比：
在画布上创建10000个圆作为测试图元。
1，四叉树搜索
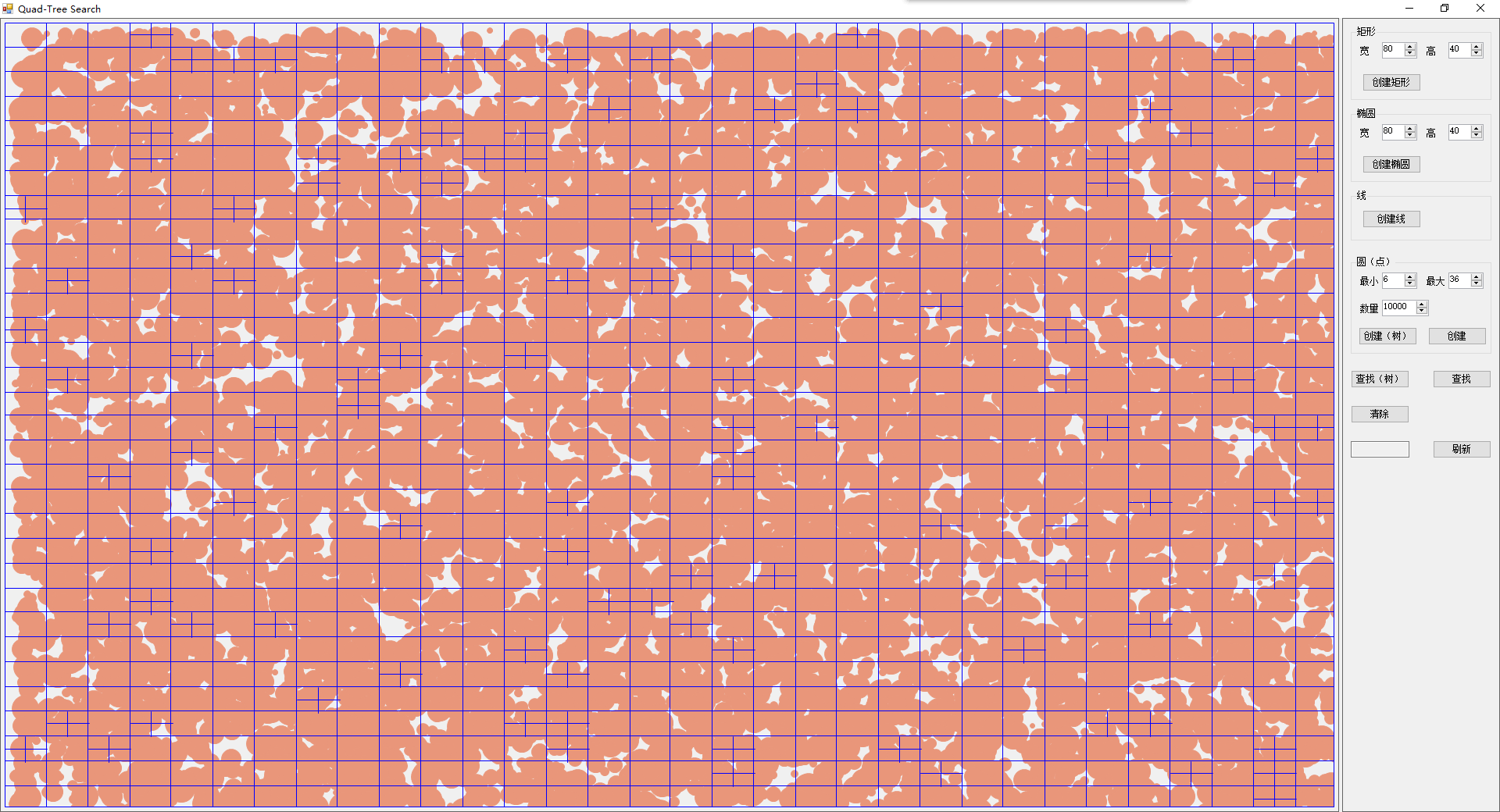
时间（毫秒）：
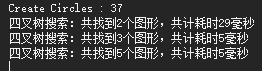
添加图元用时：37毫秒
搜索图元，第一次用时29毫秒，后续搜素都是个位数耗时。主要应该是CPU缓存的原因，后续连续搜索都是暖缓存，所以效率很高。
2，线性搜索（List，并且没有使用Parallel加速）
时间（毫秒）：
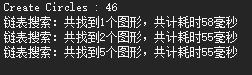
添加图元用时：46毫秒
每次搜索图元的时间效率差别不大，基本都在55到60之间。
声明：所有代码仅为本人做测试用途，如果使用此代码导致任何问题，本人概不负责。
