机器学习第四章复习
第四章
4.1 线性判据基本概念
- 生成模型

-
优势:
- 可以根据p(x)采样新的样本数据
- 可以检测出较低概率的数据,实现离群点检测
-
劣势:纬度灾难问题
-
判别模型

-
优势:快速直接、省去耗时的高维观测似然概率估计
-
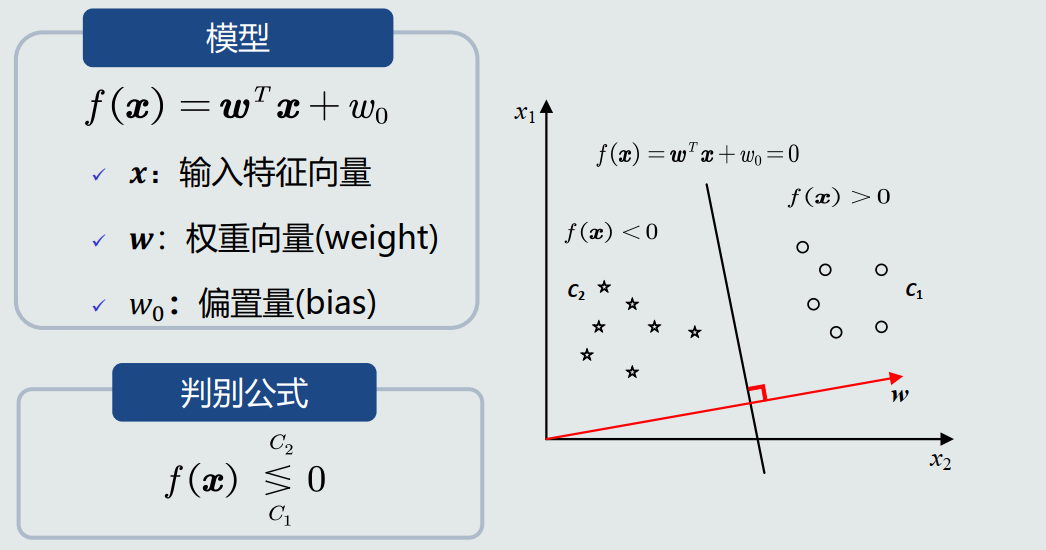
线性判据

数学表达
-
思考
-
线性模型的确定?
先确定了维数,决策边界的方向,然后用所给的样本确定具体的模型;
-
判别模型的确定要考虑哪些因素?
确定是线性和非线性。
在误差允许范围内,也可以采用线性模型处理非线性可分问题
-
原点与超平面的位置关系有哪几种?
三种,点在超平面上:W0=0;在超平面正侧:W0大于0;负侧:W0小于0;
-
4.2 线性判据学习概述
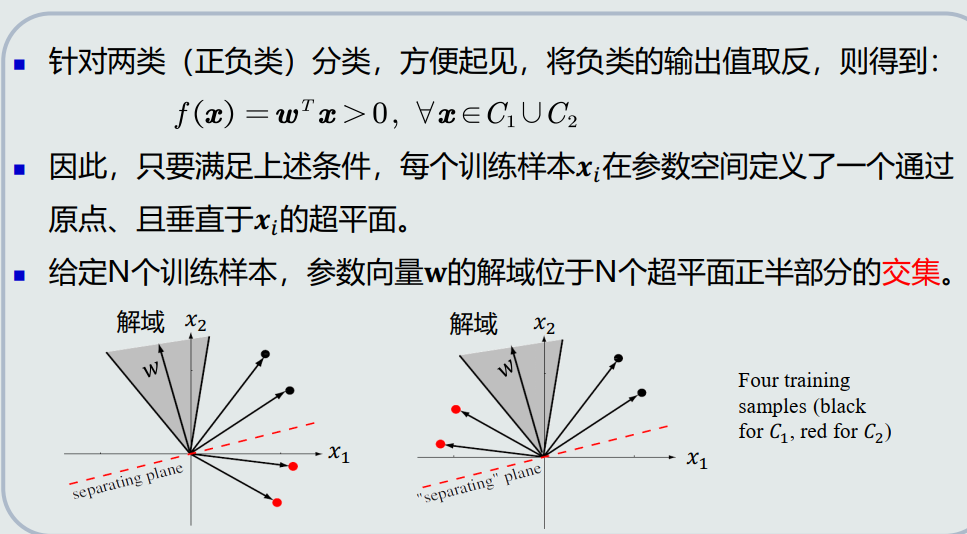
- 参数空间&解域

-
找到最优解
设计目标函数及求解

4.3 并行感知机算法
- 预处理

关于预处理的几何解释:
-
在几何上,通过在特征空间上增加一个维度,使得决策边界可以通过原点(ω0项)
-
翻转C2类样本:使得所有样本位于决策边界的同一侧
-
目标函数

- 求解方法—梯度下降法

-
算法流程
- 初始化参数:a0,步长η,阈值τ
- 迭代更新:基于当前梯度更新参数a,更新集合Yk
- 停止迭代:所有训练样本的输出值都大于0,或者更新值小于阈值τ
4.4 串行感知机算法
- 目标函数

目标函数的求解:梯度下降法
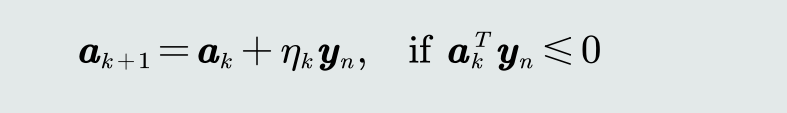
- 算法流程

-
收敛性
如果训练样本是线性可分的,感知机(并行和串行)算法理论上收敛于一个解
步长与收敛性的关系

4.5 Fisher线性判据
-
出发点:把所有的样本都投影到一维空间,使得在投影线上最易于分类 。
-
目标函数

- 参数求解


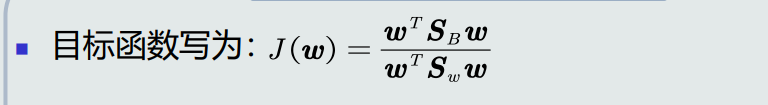
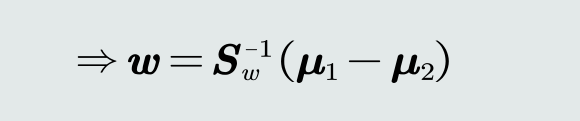
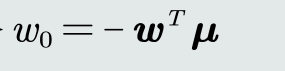

4.6 支持向量机基本概念
-
设计思想:给定一组训练样本,使得两个类中与决策边界最近的训练样本到决策边界的间隔最大
-
如何计算间隔

- 目标函数

持续更新中…



