数电——超前进位加法器

一、串行（行波）进位加法器

　　进行两个4bit的二进制数相加，就要用到4个全加器。那么在进行加法运算时，首先准备好的是1号全加器的3个input。而2、3、4号全加器的Cin全部来自前一个全加器的Cout，只有等到1号全加器运算完毕，2、3、4号全加器才能依次进行进位运算，最终得到结果。 这样进位输出，像波浪一样，依次从低位到高位传递， 最终产生结果的加法器，也因此得名为行波进位加法器（Ripple-Carry Adder，RCA）。

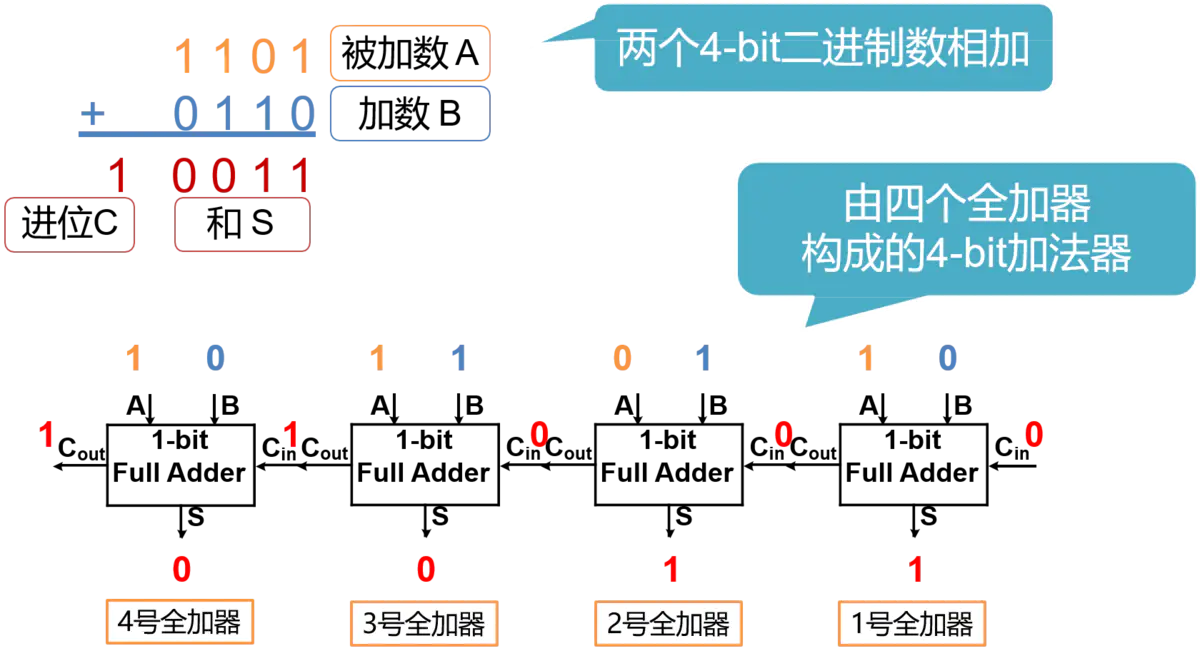
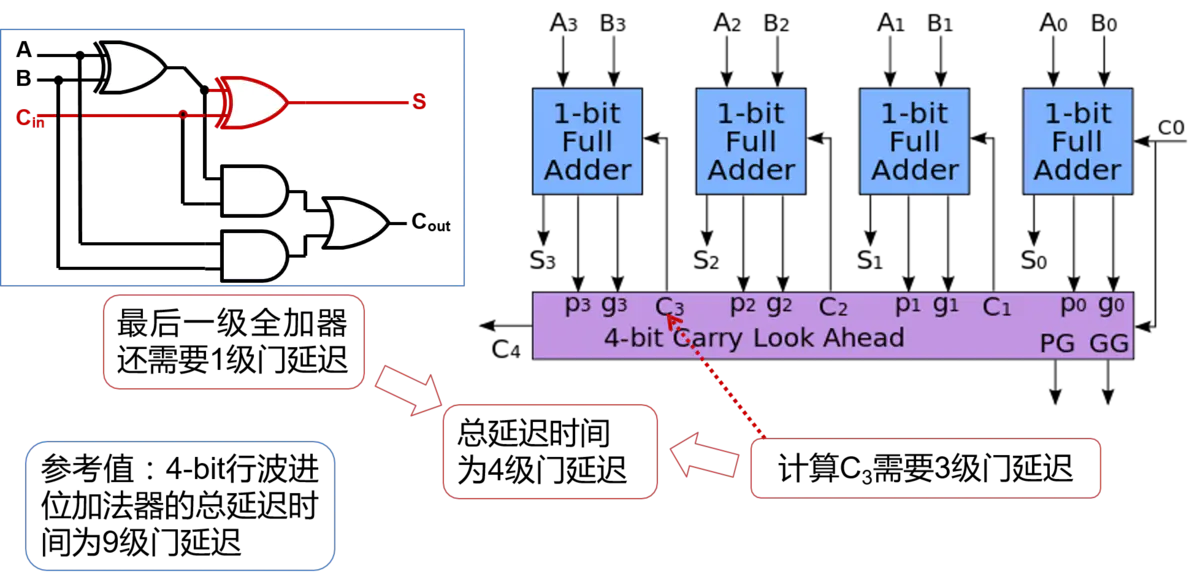
　　RCA的优点是电路布局简单，设计方便， 我们只要设计好了全加器，连接起来就构成了多位的加法器。 但是缺点也很明显，也就是高位的运算必须等待低位的运算完成， 这样造成了整个加法器的延迟时间很长。将4bit的RCA内部结构全部打开，就得到了如图所示的4-bit RCA的门电路图。要对一个电路的性能进行分析，我们就要找出其中的最长路径。 也就是找出所有的从输入到输出的电路连接中，经过的门数最多的那一条，也称为关键路径。

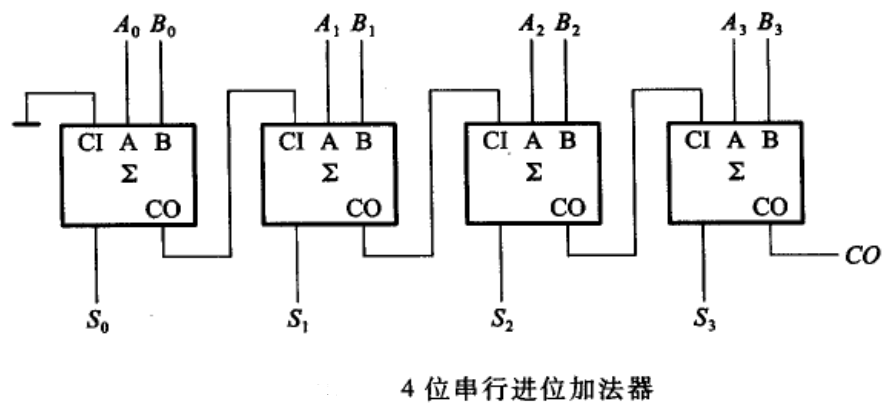
　　我们来做一个简单的分析， 对于最低位的全加器，它在A、B和Cin都已经准备好。其实，输入信号进入到这块电路之后，在连接线上传递需要花时间。 称为线延迟，而经过这样的门，也需要花时间，称为门延迟。 在进行设计原理分析时，我们主要关注门延迟。

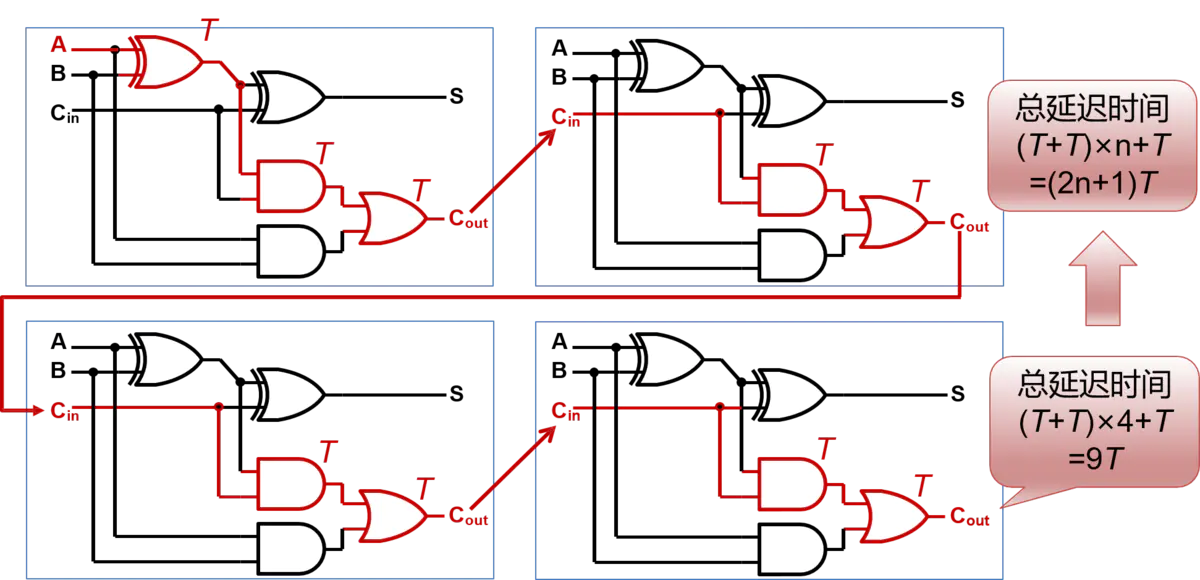
　　从第一个全加器的A-S这条通路来看，产生第一个S输出，需要通过两个门的延迟。 所以它显然不是最长的路径，当然，从A出发或着从B出发都是一样的， 所以对于第一个全加器，它的最长路径，是红色线标记的那条，后面的全加器关键路径同理可得。

　　那么，假设经过一个门电路的延迟时间为T，那么经过4个全加器所需要的总延迟时间就是：2T x 4 + T(第一个全加器产生3个T) = 9T。所以推出，经过n个全加器所产生的总延迟时间为2T x n + T = (2n+1)T。

　　对于一个32bit的RCA，有总延迟时间：(2n+1)T =(2×32+1)×T =65T，这是什么概念呢？举个例子，iPhone 5s的A7 SoC处理器采用28nm制造工艺，主频1.3GHz（0.66ns）。按照这个工艺水平，门延迟T设为0.02ns，那么32-bit RCA的延迟时间为1.3ns ，时钟频率为769MHz，远超A7处理器的主频延迟时间，更别说这个32bit的RCA只是一个加法运算器，更更别说，我们在计算过程中只考虑了门延迟，还有线延迟等各种延迟没有加入计算……

　　所以RCA的效率绝对是个问题。那么，有没有办法优化呢？RCA的主要问题是高位的运算必须等待低位的“进位输出信号”，那我们的优化思路就是‘能否提前计算出“进位输出信号’ ？”

二、超前进位加法器（Carry-Lookahead Adder，CLA）

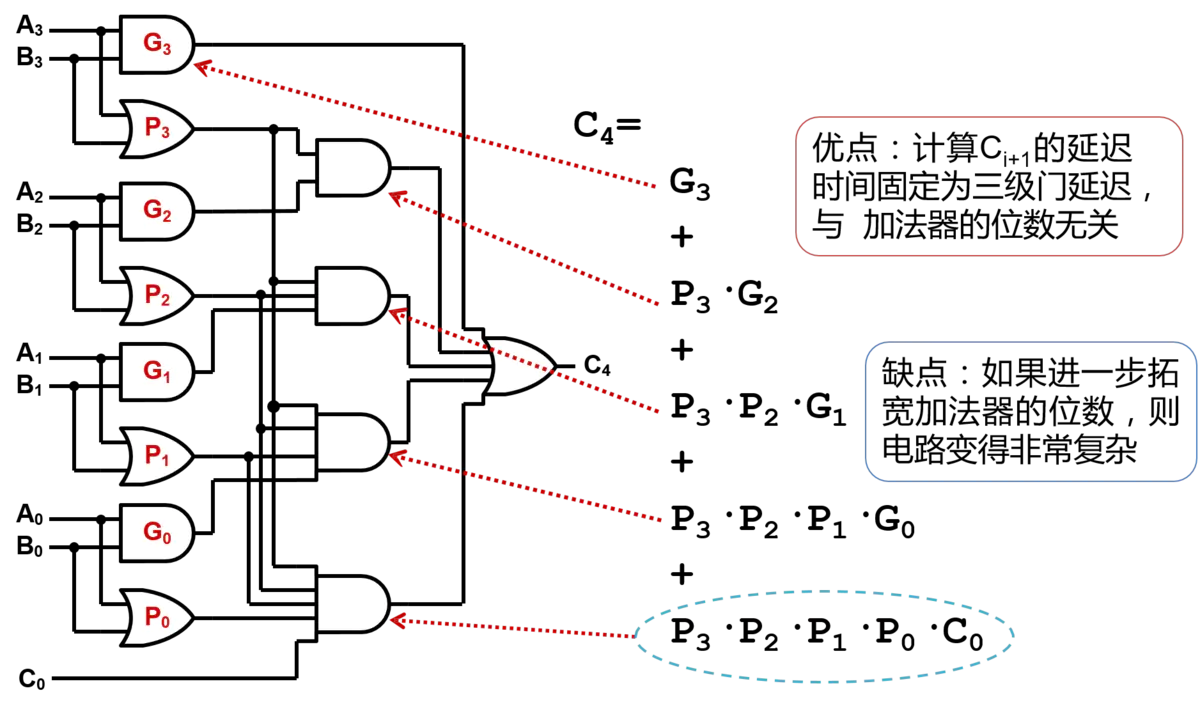
 用前一个全加器的参数来表示后面的进位输出（Cout），即：

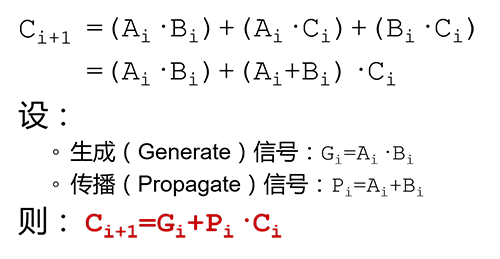
 由此来表示4个全加器的进位输出为：

　　最终我们需要得到的是C4，经过换算，C4=G3+P3·G2+P3·P2·G1+P3·P2·P1·G0+P3·P2·P1·P0·C0，而这些参数，全部已知！并不需要前一个全加器运算输出，由此我们得到了提前计算进位输出的方法， 用这样的方法实现了加法器就被称为超前进位加法器（Carry-Lookahead Adder，CLA）。

　　根据上面的优化算法，我们重新绘制了CLA的布线方式：

 

　　那么使用CLA来进行加法运算的效率如何呢？还是按照Apple A7处理器的工艺水平，单个CLA的延迟为0.08ns，4级CLA的延迟为0.26ns，时钟频率3.84GHz，都远远小于主频的延迟，完全符合标准。然而，由图可见，计算4bit的二进制数，就要平行排列4个全加器，那么要是计算8bit，16bit，32bit……的呢？可能就需要更复杂的布线方式，这就是CLA的缺点。

列表比较一下RCA和CLA的优缺点：

	RCA	CLA
结构特点	低位全加器的Cout连接到高一位全加器Cin	每个全加器的进位输入并不来自于前一级的全加器，而是来自超前进位的逻辑
优点	电路布局简单，设计方便	计算Ci+1的延迟时间固定为三级门延迟，与加法器的位数无关
缺点	高位的运算必须等待低位的运算完成，延迟时间长	如果进一步拓宽加法器的位数，则电路变得非常复杂

　　32位的加法器如果采用行波进位的方式，需要65级的门延迟， 那如果采用超前进位的方式，理想情况下也只需要四级的门延迟，但可惜的是， 这也只是一个理想。因为要实现32位的完全的超前进位，电路就会变得非常的复杂。 因此通常的实现方法， 是采用多个小规模的超前进位加法器拼接而成一个较大的加法器，例如，用4个8-bit的超前进位加法器连接成32-bit加法器。

原文链接：加法器的优化——超前进位加法器