推荐系统系列(三):FNN理论与实践
背景
在FM之后出现了很多基于FM的升级改造工作,由于计算复杂度等原因,FM通常只对特征进行二阶交叉。当面对海量高度稀疏的用户行为反馈数据时,二阶交叉往往是不够的,三阶、四阶甚至更高阶的组合交叉能够进一步提升模型学习能力。如何能在引入更高阶的特征组合的同时,将计算复杂度控制在一个可接受的范围内?
参考图像领域CNN通过相邻层连接扩大感受野的做法,使用DNN来对FM显式表达的二阶交叉特征进行再交叉,从而产生更高阶的特征组合,加强模型对数据模式的学习能力 [1]。这便是本文所要介绍的FNN(Factorization Machine supported Neural Network)模型,下面将对FNN进行详细介绍。
分析
1. FNN 结构
FNN的思想比较简单,直接在FM上接入若干全连接层。利用DNN对特征进行隐式交叉,可以减轻特征工程的工作,同时也能够将计算时间复杂度控制在一个合理的范围内。
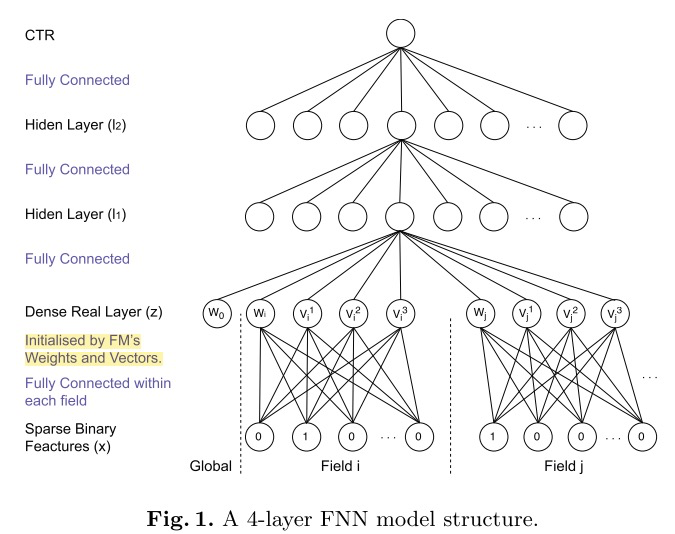
为了加速模型的收敛,充分利用FM的特征表达能力,FNN采用了两阶段训练方式。首先,针对任务构建FM模型,完成模型参数的学习。然后,将FM的参数作为FNN底层参数的初始值。这种两阶段方式的应用,是为了将FM作为先验知识加入到模型中,防止因为数据稀疏带来的歧义造成模型参数偏差。
However, according to [21], if the observational discriminatory information is highly ambiguous (which is true in our case for ad click behaviour), the posterior weights (from DNN) will not deviate dramatically from the prior (FM).
通过结构图可以看到,在特征进行输入之前首先进行分域操作,这种方式也成了后续处理高维稀疏性数据的通用做法,目的是为了减少模型参数量,与FM计算过程保持一致。
模型中的 \(Dense Real Layer\) 将FM产出的低维稠密特征向量进行简单拼接,作为下一全连接层的输入,采用 \(tanh\) 激活函数,最终使用 \(sigmoid\) 将输出压缩至0~1之间作为预测。
2. 优缺点
优点:
- 引入DNN对特征进行更高阶组合,减少特征工程,能在一定程度上增强FM的学习能力。这种尝试为后续深度推荐模型的发展提供了新的思路(相比模型效果而言,个人感觉这种融合思路意义更大)。
缺点:
- 两阶段训练模式,在应用过程中不方便,且模型能力受限于FM表征能力的上限。
- FNN专注于高阶组合特征,但是却没有将低阶特征纳入模型。
仔细分析下这种两阶段训练的方式,存在几个问题:
1)FM中进行特征组合,使用的是隐向量点积。将FM得到的隐向量移植到DNN中接入全连接层,全连接本质是将输入向量的所有元素进行加权求和,且不会对特征Field进行区分,也就是说FNN中高阶特征组合使用的是全部隐向量元素相加的方式。说到底,在理解特征组合的层面上FNN与FM是存在Gap的,而这一点也正是PNN对其进行改进的动力。
2)在神经网络的调参过程中,参数学习率是很重要的。况且FNN中底层参数是通过FM预训练而来,如果在进行反向传播更新参数的时候学习率过大,很容易将FM得到的信息抹去。个人理解,FNN至少应该采用Layer-wise learning rate,底层的学习率小一点,上层可以稍微大一点,在保留FM的二阶交叉信息的同时,在DNN上层进行更高阶的组合。
3. 参数调优
根据论文中的实验来看,性能影响最大的超参数为:1)DNN部分的网络结构;2)dropout比例;
个人认为,该论文中超参数对比试验做的并不严谨,以下结论仅供参考。
1)DNN部分的网络结构
对比四种网络结构,最佳的网络结构为 \(Diamond\) .
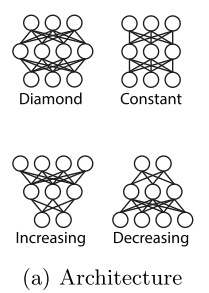
2)dropout比例
Dropout的效果要比L2正则化更好,且FNN最佳dropout比例为0.8左右。

实验
依旧使用 \(MovieLens100K dataset\) ,核心代码如下。
class FNN(object):
def __init__(self, vec_dim=None, field_lens=None, lr=None, dnn_layers=None, dropout_rate=None, lamda=None):
self.vec_dim = vec_dim
self.field_lens = field_lens
self.field_num = len(field_lens)
self.lr = lr
self.dnn_layers = dnn_layers
self.dropout_rate = dropout_rate
self.lamda = float(lamda)
self.l2_reg = tf.contrib.layers.l2_regularizer(self.lamda)
assert dnn_layers[-1] == 1
self._build_graph()
def _build_graph(self):
self.add_input()
self.inference()
def add_input(self):
self.x = [tf.placeholder(tf.float32, name='input_x_%d'%i) for i in range(self.field_num)]
self.y = tf.placeholder(tf.float32, shape=[None], name='input_y')
self.is_train = tf.placeholder(tf.bool)
def inference(self):
with tf.variable_scope('fm_part'):
emb = [tf.get_variable(name='emb_%d'%i, shape=[self.field_lens[i], self.vec_dim], dtype=tf.float32, regularizer=self.l2_reg) for i in range(self.field_num)]
emb_layer = tf.concat([tf.matmul(self.x[i], emb[i]) for i in range(self.field_num)], axis=1)
x = emb_layer
in_node = self.field_num * self.vec_dim
with tf.variable_scope('dnn_part'):
for i in range(len(self.dnn_layers)):
out_node = self.dnn_layers[i]
w = tf.get_variable(name='w_%d'%i, shape=[in_node, out_node], dtype=tf.float32, regularizer=self.l2_reg)
b = tf.get_variable(name='b_%d'%i, shape=[out_node], dtype=tf.float32)
x = tf.matmul(x, w) + b
if out_node == 1:
self.y_logits = x
else:
x = tf.layers.dropout(tf.nn.relu(x), rate=self.dropout_rate, training=self.is_train)
in_node = out_node
self.y_hat = tf.nn.sigmoid(self.y_logits)
self.pred_label = tf.cast(self.y_hat > 0.5, tf.int32)
self.loss = -tf.reduce_mean(self.y*tf.log(self.y_hat+1e-8) + (1-self.y)*tf.log(1-self.y_hat+1e-8))
reg_variables = tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)
if len(reg_variables) > 0:
self.loss += tf.add_n(reg_variables)
self.train_op = tf.train.AdamOptimizer(self.lr).minimize(self.loss)
reference
[1] Zhang, Weinan, Tianming Du, and Jun Wang. "Deep learning over multi-field categorical data." European conference on information retrieval. Springer, Cham, 2016.
知识分享
个人知乎专栏:https://zhuanlan.zhihu.com/c_1164954275573858304
欢迎关注微信公众号:SOTA Lab
专注知识分享,不定期更新计算机、金融类文章




