Python入门篇-数据结构树（tree）篇

　　　　　　　　　　　　　　　Python入门篇-数据结构树（tree）篇

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　作者：尹正杰

版权声明：原创作品，谢绝转载！否则将追究法律责任。

 

 

一.树概述

1>.树的概念

非线性结构，每个元素可以有多个前躯和后继

树是n（n>=0）个元素的集合：
    n = 0时，称为空树
    树只有一个特殊的没有前驱的元素，称为树的根root
    树中除了根结点外，其余元素只能有一个前驱，可以有零个或者多个后继

递归定义：
    数T是n（n>=0）个元素的集合。n=0时，称为空树
    有且只有一个特殊元素根，剩余元素都可以被划分为m个互不相交的集合T1,T2,T3,...,Tm，而每一个集合都是树，称为T的子树subtree
    子树也有自己的根

2>.数的相关术语

结点：
　　树中的数据元素。

结点的度degree:
　　结点拥有的子树的数目称为度，记作d（v）。

叶子结点：
　　结点的度为0，称为叶子结点leaf，终端结点，末端结点。

分支结点：
　　结点的度不为0，称为非终端结点或分支结点。

分支：
　　结点之间的关系。

内部结点：
　　除根结点外的分支结点，当然也不包括叶子结点。

如下图所示，数的度是树内各结点的度的最大值。D结点度最大为3，树的度数就是3.　　　

 

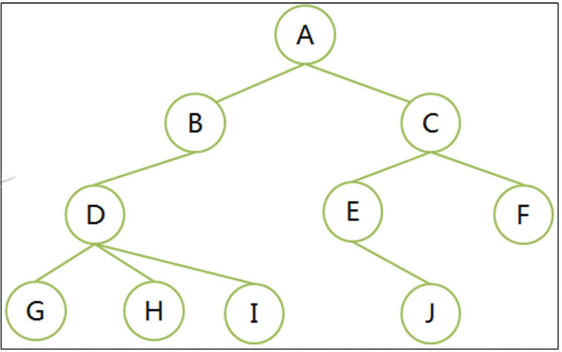
孩子结点（儿子Child）结点：
　　结点的子树的根结点称为该结点的孩子。

双亲（父Parent）结点:
　　一个结点是它各子树的根结点的双亲。

兄弟（Sibling）结点：
　　具有相同双亲结点的节点。

祖先节点：
　　从根结点到该结点所有分支上所有的节点，如上图所示:A,B,D都是G的祖先结点。

子孙结点：
　　结点的所有子树上的结点称为该结点的子孙。B的子孙是D,G,H,I

结点的层次（Level）：
　　根节点为第一层，根的孩子为第二层，以此类推，记作L（v）。

树的深度（高度Depth）：
　　树的层次的最大值。上图的树深度为4.

堂兄弟：
　　双亲在同一层的结点。

有序树：
　　结点的子树是有顺序的（兄弟有大小，有先后次序），不能交换。

无序树：
　　结点的子树是有无序的，可以交换。

路径：
　　书中的k个节点n1,n2,n3,...,nk，满足ni是n（i+1）的双亲，称为n1到nk的一条路径。就是一条线串下来的，前一个都是后一个的父（前驱）结点。

路径的长度
　　路径的长度 = 路径上结点点数 -1，也是分支数。

森林：
　　m（m>=0）棵不想交的树的集合。对于节点而言，其子树的结合就是森林。A节点的2棵子树的集合就是森林。

3>.数的特点

    （1）唯一的根
    （2）子树不相交
    （3）除了根以外，每个元素只能有一个前驱，可以有零个或多个后继
    （4）根结点没有双亲结点（前驱），叶子结点没有孩子结点（后继）
    （5）vi是vj的双亲，则L（vi）=L（vj）-1，也就是说双亲比孩子结点的层次小1

 

二.树的分类

1>.二叉树

（1）每个结点最多2棵子树
　　　　二叉树不存在度数大于2的结点。

（2）它是有序树，左子树，右子树是顺序的，不能交换次序

（3）即使某个节点只有一棵子树，也要确定它是左子树还是右子树

（4）二叉树的物种基本形态
　　　　1）空二叉树
　　　　2）只有一个根结点
　　　　3）根结点只有左子树
　　　　4）根结点只有右子树
　　　　5）根结点有左子树和右子树

 

2>.斜树

左斜树
　　所有节点都只有左子树

右斜树
　　所有节点都只有右子树

3>.满二叉树

（1）一颗二叉树的所有分支结点都存在左子树和右子树，并且所有子节点只存在在最下面一层。

（2）同样深度二叉树中，满二叉树结点最多。

（3）K为深度（1<=k<=n）,则节点总数为2^k-1

如下图，一个深度为4的15个节点的满二叉树

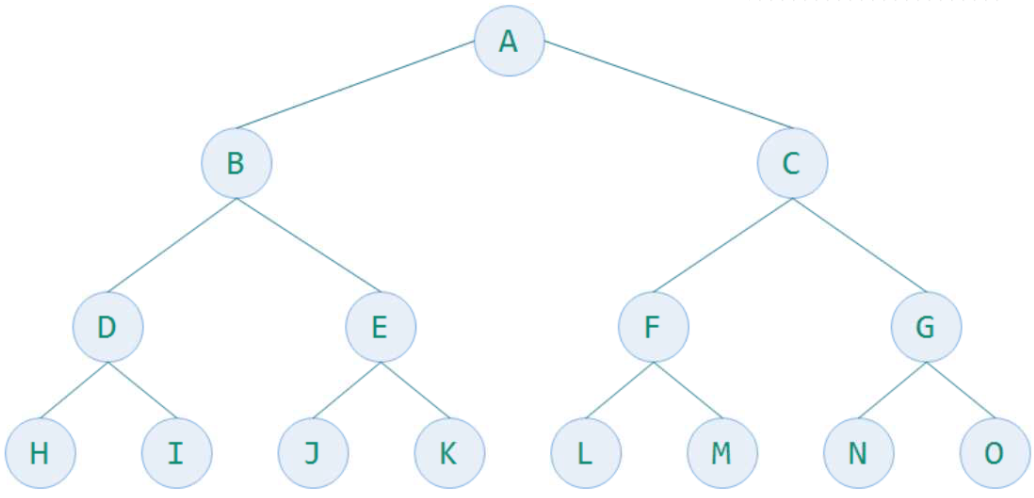
4>.完全Complete Binary Tree

若二叉树的深度为k，二叉树的层数从1到k-1层的节点数都达到了最大个数，在第k层的所有节点都集中在最左边，这就是完全二叉树。

完全二叉树由满二叉树引出。

满二叉树一定是完全二叉树，但完全二叉树不是满二叉树。

k为深度（1<=k<=n），则结点总数最大值为2^k-1,当达到最大值的时候就是满二叉树。

如下图所示，完全二叉树，最下一层的叶子结点都连续的集中在左边

 

 

三.二叉树性质

1>.性质1

　　在二叉树的第i层上最多有2^（i-1）个节点（i>=1）\

2>.性质2

　　深度为k的二叉树，至多有2^k-1个结点（k>=1）
　　一层：2 - 1 = 1
　　二层：4 - 1 = 1 + 2 =3
　　三层：8 - 1 = 1 + 2 + 4 = 7

3>.性质3

    对任何一棵二叉树T，如果其终结结点数为n0，度数为2的节点为n2，则有n0 = n2 + 1.
　　换句话说，就是叶子结点数-1就等于度数为2的结点数。
　　证明：
　　　　（1）总结点数为n = n0 + n1 + n2，n1位度数为1的节点总数。
　　　　（2）一棵树的分支为n-1，因为除了根结点外，其余结点都有一个分支，即n0 + n2 + n3 -1.
　　　　（3）分支数还等于n0*0 + n1*1 +n2*2,n2是2分支结点所以乘以2,2*n2 + n1.
　　　　（4）可得2*n2 + n1 = n0 + n1 + n2 -1 => n2 = n0 -1

4>.性质4

　　具有n个结点的完全二叉树的深度为int(log2n)+1或者math.ceil(log2(n+1))

5>.性质5

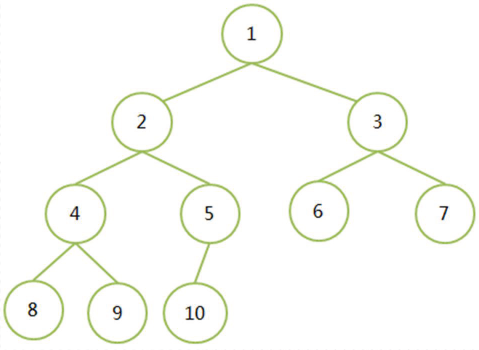
　　（1）如果有一棵n个结点的完全二叉树（深度为性质4），按照节点层次编号，如下图所示。
　　（2）如果i=1，则节点i是二叉树的根，无双亲；如果i>1，则其双亲是int(i/2)，向下取整。就是子结点的编号整除2得到的就是父节点的编号。父结点如果是i，那么左孩子结点就是2i，右孩子结点就是2i+1.
　　（3）如果2i>n,则节点i无左孩子，即结点i为叶子结点；否则其左孩子结点存在编号为2i。
　　（4）如果2i+1>n,则结点i无右孩子，注意这里并不能说明结点i没有左孩子；否则右孩子节点存在编号为2i+1。

6>.其他性质

　　（1）高度为k的二叉树，至少有k个结点。
　　（2）含有n（n>=1）的结点的二叉树高度至多为n。
　　（3）含有n（n>=1）的结点的二叉树的高度至多为n，最少为math.ceil(log2(n+1)),不小于对数值的最小整数，向上取整。
　　（4）假设高度为h，2^h-1=n => h = log2(n+1)，层次数是取整。如果是8个节点，3.1699就要向上取整为4，为4层。