初赛选择题知识点整理 & 听课笔记
初赛知识点整理(选择题)& 听课笔记
一、计算机基础
-
第一台计算机 埃尼阿克 1946
-
第一个程序员 Ada(女)
-
菲尔兹奖(数学)
-
IEEE:美国电气与电子工程师协会
-
图灵奖 华人只有姚期智 艾伦·麦席森·图灵(英)ACM设立
-
冯诺依曼结构:
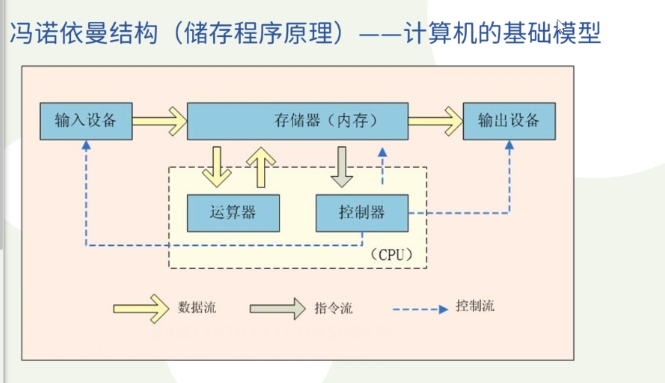
-
计算机组成:
- 主频:处理速度
- 内存:临时存放的东西(RAM)
- 外存
- 摩尔定律:硬盘每18个月翻倍
-
软件:
- 操作系统:Windows、DOS、Unix、Linux、MacOS、Android、ios、鸿蒙
- 应用软件
- 机器语言(CPU看得懂的指令)、汇编语言、高级语言(c++)
-
文字编码:GBK编码(2字节)(比较老的)、utf-8(3字节)(比较新)
-
图片:黑白(01)、24位彩色(RGB)
-
文件系统扩展名(不常见的):
- 图片:tiff,jpeg
- 文档:PDF(不可编辑)
- 视频:avi,rm,WMV,MPEG
-
关于比赛:
- NOI:1984开始
- NOIP:1995开始
- 2022年后只能用c++
-
程序设计:
- 编译:代码->可执行文件(机器码) C/C++,Pascal:编译型语言 编译器:将一种语言(通常是高级语言)翻译成另一种语言(通常是低级语言)
- 解释:一行一行运行,又被称为“脚本“,后面错了仍可以进行前面的部分。 Python,JavaScript,PHP,BASIC:解释型语言
-
存储:KiB、MiB、GiB-->1024,KB、MB、GB-->1000。
二、基础算法
- 排序
- 计数排序(人们口中的“桶排序”):$O(n+maxx) $不基于比较,稳定
- 基数排序:从个位开始进行计数排序。\(O(kn)\) 稳定
- 选择排序:选最小的与第一张交换,再选次小的。\(O(n^2)\) 不稳定
- 冒泡排序:左右比较不断交换,最大的先到最右边,然后次大的到次右边。$O(n^2) $稳定
- 插入排序:跟打扑克一样。$O(n^2) $ 稳定
- 希尔排序:插入排序的优化版,\(O(n)\to O(nlog^2n)\),不稳定
- O(nlogn)排序:归并(稳定),快速排序堆排序(不稳定),快排最慢 \(O(n^2)\)(当原数组有序时)
- 卡特兰数:n个数出栈方案数
三、排列组合问题
-
捆绑法:例如x个元素必须靠在一起。则把这x个元素单独拿出来,方案数为 \((n-x)!\times x!\)。
-
插板法:例如10个人分到7个班,每班至少一人,则10个人9个空插6个板,方案数为\(C_9^6\)。
注意:插板法只能解决人相同班级不同的类型的问题,不能解决都相同或都不同的问题!
-
分类法:例如csp2019提高t7,分类讨论结合排列组合。
-
可以考虑画图表进行手动dp。
-
卡特兰数:
-
含义为n*n的方格中从左下角走到右上角的方案数(要求向上或向右走,且每时每刻向右走的次数大于等于向上的次数)
-
\(Ans=C_{2n}^n-C_{2n}^{n-1}(n\in Z)\)
-
推导:容斥原理。
-
-
错排问题:
- 公式:\(Ans=n!-\frac{n!}{2!}+\frac{n!}{3!}-……+(-1)^{n+1}\frac{n!}{n!}\)
- 考虑容斥。
-
看着选项数字都很小直接枚举即可。
四、其他数学问题
-
负数补码=原码-1 再取反。若忘记了可以通过a+(-a)=0推出。
-
生动形象的补码图
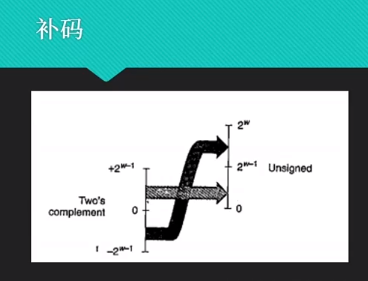
-
主定理:
-
\(\Theta\) 是平均时间复杂度(准确),\(\Omicron\) 是最坏情况下的复杂度(上界),\(\Omega\) 是最好情况下的复杂度(下界)。
-
\(T(n)=aT(\frac{n}{b})+f(n)\)
-
第一步:算出 \(\log_{b}a\) ,与 \(f(n)\) 中n的幂次作比较
-
第二步:
- 若 \(\log_{b}a > f(n)\)的幂次,则 \(T(n)=\Theta(n^{\log_{b}a})\)
- 若 \(\log_{b}a = f(n)\)的幂次,则 \(T(n)=\Theta(n^{\log_{b}a}\log n)\)
- 若 \(\log_{b}a < f(n)\)的幂次,则 \(T(n)=\Theta(f(n))\)
-
好用!
-
-
pascal公式:\(C_n^m=C_{n-1}^{m-1}+C_{n-1}^{m}\) 理解:第n个数选或者不选两种情况。


