洛谷 P4281 [AHOI2008]紧急集合 / 聚会（树剖，LCA）
传送门
解题思路
题目很长，实际上就是给你一棵树，然后给你三个点，让你找到一个点，是这个点到三个点的距离和最短。
很显然的是，这个点在这三个点简单路径的上，而这三条简单路径一定有且只有一个交汇点，这个交汇点就是答案。
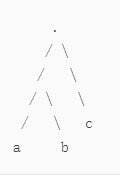
这就是为什么一定有一个交点，而且这个交点是其中两个点的LCA，且这个LCA是深度最深的LCA。
因为如果取深度较浅的LCA，则a，b两点交汇后要一同走一段路程，花费两个人的金币，就不如让c多走一段距离了。
而深度较浅的那个点，一定就是三个LCA r1,r2,r3 中与其他两个不相同的那个LCA。（r1==r2==r3的情况特判）。
AC代码
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 const int maxn=500005; 6 int n,m,fa[maxn],dep[maxn],son[maxn],p[maxn],tp[maxn],cnt,size[maxn]; 7 struct node{ 8 int v,next; 9 }e[maxn*2]; 10 void insert(int u,int v){ 11 cnt++; 12 e[cnt].v=v; 13 e[cnt].next=p[u]; 14 p[u]=cnt; 15 } 16 void dfs1(int u,int dad,int deep){ 17 int maxsize=0; 18 fa[u]=dad; 19 dep[u]=deep; 20 size[u]=1; 21 for(int i=p[u];i!=-1;i=e[i].next){ 22 int v=e[i].v; 23 if(v==dad) continue; 24 dfs1(v,u,deep+1); 25 size[u]+=size[v]; 26 if(size[v]>maxsize){ 27 son[u]=v; 28 maxsize=size[v]; 29 } 30 } 31 } 32 void dfs2(int u,int top){ 33 tp[u]=top; 34 if(son[u]) dfs2(son[u],top); 35 for(int i=p[u];i!=-1;i=e[i].next){ 36 int v=e[i].v; 37 if(v==fa[u]||v==son[u]) continue; 38 dfs2(v,v); 39 } 40 } 41 int getrt(int x,int y){ 42 while(tp[x]!=tp[y]){ 43 if(dep[tp[x]]<dep[tp[y]]) swap(x,y); 44 x=fa[tp[x]]; 45 } 46 return dep[x]>dep[y]?y:x; 47 } 48 int main(){ 49 memset(p,-1,sizeof(p)); 50 cin>>n>>m; 51 for(int i=1;i<n;i++){ 52 int u,v; 53 scanf("%d%d",&u,&v); 54 insert(u,v); 55 insert(v,u); 56 } 57 dfs1(1,-1,1); 58 dfs2(1,1); 59 for(int i=1;i<=m;i++){ 60 int a,b,c; 61 scanf("%d%d%d",&a,&b,&c); 62 int r1=getrt(a,b); 63 int r2=getrt(a,c); 64 int r3=getrt(b,c); 65 int ans=dep[a]+dep[b]+dep[c]-dep[r1]-dep[r2]-dep[r3]; 66 if(r1==r2) printf("%d %d\n",r3,ans); 67 else if(r1==r3) printf("%d %d\n",r2,ans); 68 else if(r2==r3) printf("%d %d\n",r1,ans); 69 } 70 return 0; 71 }
//AHOI 2008
