洛谷 P3384 【模板】轻重链剖分(树链剖分)
传送门
树链剖分
简单点说,就是把一棵树变成多条链。
这里说的是重链剖分。
在遍历一颗树的时候,我们强制从父亲节点走向儿子时,先走所有儿子中以儿子为根的子树最大的那个儿子。
其他的儿子不管什么顺序都可。
这样就可以把dfs序作为链。
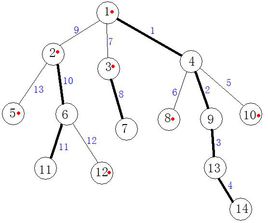
例如上面这棵树,边上的蓝色数字就是遍历顺序。
说一些定义:
重边:父亲结点和重儿子连成的边;
轻边:父亲节点和轻儿子连成的边;
重链:由多条重边连接而成的路径;
轻链:由多条轻边连接而成的路径;
在上图中,黑色边就是重边。1-4-9-13-14就是一条重链,2-6-11也是一条重链,3-7也是一条重链。
我们把这些链用某种数据结构存起来,例如线段树,就可以去做一些lca、区间操作了。
怎么进行树剖呢?
我们需要两个dfs,第一个处理好以每个节点为根的子树的大小并求出每一个节点的重儿子是谁,为下一个dfs做准备。
第二个根据规定的遍历顺序遍历这棵树,并把每个点的是第几个遍历的记下来id[]。
同时还要记录下遍历顺序对应的节点编号rk[]; 很显然,rk[a]=b,id[b]=a;
同时还要记录下每个节点所在链的链顶是哪个节点(这是保证效率的关键)
树剖用法
树剖一般不会单独使用,会和其他的算法一起,比如说用线段树存链,能快速找到两个节点的最近公共祖先,从而在这两个节点的路径上做一些区间操作。
这个题就是这样。
AC代码
1 #include<iostream> 2 #include<cstring> 3 #include<iomanip> 4 using namespace std; 5 const int maxn=100005; 6 int n,m,r,mod,p[maxn],va[maxn],cnt; 7 long long lazy[maxn*4]; 8 int rk[maxn],id[maxn],dp[maxn],size[maxn],son[maxn],topp[maxn],f[maxn]; 9 long long s[maxn*4]; 10 struct node{ 11 int v,next; 12 }e[maxn*2]; 13 void insert(int u,int v){ 14 cnt++; 15 e[cnt].v=v; 16 e[cnt].next=p[u]; 17 p[u]=cnt; 18 } 19 void dfs1(int fa,int u,int deep){ 20 f[u]=fa; 21 dp[u]=deep; 22 size[u]=1; 23 son[u]=0; 24 for(int i=p[u];i!=-1;i=e[i].next){ 25 if(e[i].v==fa) continue; 26 dfs1(u,e[i].v,deep+1); 27 size[u]+=size[e[i].v]; 28 if(size[e[i].v]>size[son[u]]) son[u]=e[i].v; 29 } 30 } 31 void dfs2(int fa,int u,int top){ 32 cnt++; 33 id[u]=cnt; 34 rk[cnt]=u; 35 topp[u]=top; 36 if(!son[u]) return; 37 dfs2(u,son[u],top); 38 for(int i=p[u];i!=-1;i=e[i].next){ 39 if(e[i].v==fa||e[i].v==son[u]) continue; 40 dfs2(u,e[i].v,e[i].v); 41 } 42 } 43 void pushdown(int id,int l,int r){ 44 int mid=(l+r)>>1; 45 s[id<<1]+=lazy[id]*(mid-l+1); 46 s[id<<1|1]+=lazy[id]*(r-mid); 47 lazy[id<<1]+=lazy[id]; 48 lazy[id<<1|1]+=lazy[id]; 49 lazy[id<<1]%=mod; 50 lazy[id<<1|1]%=mod; 51 lazy[id]=0; 52 } 53 void build(int id,int l,int r){ 54 if(l==r){ 55 s[id]=va[rk[l]]; 56 return; 57 } 58 int mid=(l+r)/2; 59 build(id*2,l,mid); 60 build(id*2+1,mid+1,r); 61 s[id]=(s[id*2]+s[id*2+1])%mod; 62 } 63 void add(int idd,int l,int r,int x,int y,int value){ 64 if(x<=l&&r<=y){ 65 s[idd]+=(r-l+1)*value; 66 s[idd]%=mod; 67 lazy[idd]+=value; 68 lazy[idd]%=mod; 69 return; 70 } 71 int mid=(l+r)>>1; 72 pushdown(idd,l,r); 73 if(x<=mid) add(idd<<1,l,mid,x,y,value); 74 if(mid<y) add(idd<<1|1,mid+1,r,x,y,value); 75 s[idd]=s[idd*2]+s[idd*2+1]; 76 s[idd]%=mod; 77 } 78 int query(int idd,int l,int r,int x,int y){ 79 if(x<=l&&r<=y){ 80 return s[idd]%mod; 81 } 82 int mid=(l+r)>>1,ans=0; 83 pushdown(idd,l,r); 84 if(x<=mid) ans+=query(idd<<1,l,mid,x,y); 85 ans%=mod; 86 if(mid<y) ans+=query(idd<<1|1,mid+1,r,x,y); 87 return ans%mod; 88 } 89 int main() 90 { 91 memset(p,-1,sizeof(p)); 92 cin>>n>>m>>r>>mod; 93 for(int i=1;i<=n;i++) cin>>va[i]; 94 for(int i=1;i<n;i++){ 95 int U,V; 96 cin>>U>>V; 97 insert(U,V); 98 insert(V,U); 99 } 100 dfs1(-1,r,1); 101 cnt=0; 102 dfs2(-1,r,r); 103 build(1,1,n); 104 for(int i=1;i<=m;i++){ 105 int t,x,y,z; 106 cin>>t; 107 if(t==1){ 108 cin>>x>>y>>z; 109 z%=mod; 110 while(topp[x]!=topp[y]){ 111 if(dp[topp[x]]<dp[topp[y]])swap(x,y); 112 add(1,1,n,id[topp[x]],id[x],z); 113 x=f[topp[x]]; 114 } 115 if(dp[x]>dp[y])swap(x,y); 116 add(1,1,n,id[x],id[y],z); 117 } 118 if(t==2){ 119 cin>>x>>y; 120 long long ans=0; 121 while(topp[x]!=topp[y]){ 122 if(dp[topp[x]]<dp[topp[y]])swap(x,y); 123 ans+=query(1,1,n,id[topp[x]],id[x]); 124 ans%=mod; 125 x=f[topp[x]]; 126 } 127 if(dp[x]>dp[y])swap(x,y); 128 ans+=query(1,1,n,id[x],id[y]); 129 cout<<ans%mod<<endl; 130 } 131 if(t==3){ 132 cin>>x>>z; 133 add(1,1,n,id[x],id[x]+size[x]-1,z); 134 } 135 if(t==4){ 136 cin>>x; 137 cout<<query(1,1,n,id[x],id[x]+size[x]-1)%mod<<endl; 138 } 139 } 140 return 0; 141 }

