洛谷 P1983 车站分级(拓扑排序)

题目链接

https://www.luogu.org/problemnew/show/P1983

题目描述

一条单向的铁路线上，依次有编号为 1,2,…,n的 n个火车站。每个火车站都有一个级别，最低为1 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 x，则始发站、终点站之间所有级别大于等于火车站x 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）

例如，下表是5 趟车次的运行情况。其中，前4 趟车次均满足要求，而第 5趟车次由于停靠了 3 号火车站（2级）却未停靠途经的 6 号火车站（亦为 2 级）而不满足要求。

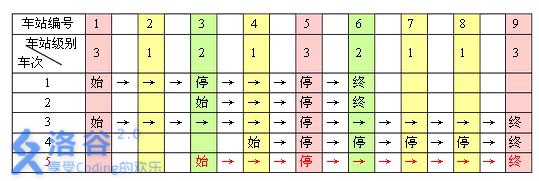
现有 m趟车次的运行情况（全部满足要求），试推算这n 个火车站至少分为几个不同的级别。

输入输出格式

输入格式：

第一行包含 2个正整数 n,m用一个空格隔开。

第 i+1行(1≤i≤m)中，首先是一个正整数 si(2≤si≤n)，表示第i 趟车次有 si个停靠站；接下来有si​个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式：

一个正整数，即 n个火车站最少划分的级别数。

输入输出样例

输入样例#1：

9 2 
4 1 3 5 6 
3 3 5 6 

输出样例#1：

2

输入样例#2：

9 3 
4 1 3 5 6 
3 3 5 6 
3 1 5 9 

输出样例#2：

3

说明

对于20% 的数据，1≤n,m≤10；

对于 50%的数据，1≤n,m≤100；

对于 100%的数据，1≤n,m≤1000。

解题思路

首先第一眼看到这个题，就知道这是这是拓扑排序（当时在讲拓扑排序），但是此题最难的地方在于建边：对于给定的两个车站(起点站和终点站)，必须先停在这两个车站之间所有>=这两个车站的车站，但是还有一个等于，所以我们需要换一种思路。既然停下的是所有大于等于起点站和终点站级别的车站，那么也就是说，没停下的车站的级别一定是小于起点站和终点站的，又因为起点站和终点站的级别小于等于中间停下的车站，所以最终的出结论，没停下的车站一定是小于停下的所有的车站的级别(包括起点站和终点站)，换句话说，停下的所有车站的级别一定>未停下的的车站的级别。

我们看到了>，就表明可以用拓扑排序来完成了。

本题还有一个难点就是需要优化，设想当多趟列车经过了相同的站点时，很可能会炸空间——记录入度的数组。所以我们需要在每一次建边前，先判断一下这两个车站是否已经有了边了，如果有了边了，那么记录入读的数组也不需要再加一了。

最后进行一遍有点变动的拓扑排序：用入度为0的点去更新与它相邻的点的级别。（我总感觉像求最短路）。

总结一下，这个题最难的地方就是建图和优化。

最后，附上AC代码（带有解析）。

 

#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
int n,m,k,in[1005];                //k是每一趟车停下的车站数。in[i]存的是点的入度(拓扑排序用)。
int gragh[1005][1005],tou,wei;    //gragh存图,这里是邻接矩阵存图。tou是每一趟列车的始发站，wei是终点站。
int stop[1005],vis[1005];        //stop存的是每一趟车停下的车站，vis[j]存的是车站j有没有停下。
int ans,level[1005];            //level[i]存的是第i个车站的等级。ans存的是level中的最大值。
queue<int> q;                    //拓扑排序用，保证队列里的点都是入度为0的点 
int main()
{
cin>>n>>m;
for(int i=1;i<=m;i++){
    tou=0,wei=0;
    memset(vis,0,sizeof(vis));    //每次把标记数组和停靠的车站数组清空。
    memset(stop,0,sizeof(stop));
    scanf("%d",&k);
    for(int j=1;j<=k;j++){
        scanf("%d",&stop[j]);
        vis[stop[j]]=1;            //标记读入的这个车站停靠过。 
        if(j==1) tou=stop[j];    //记录下起始站和终点站。 
        if(j==k) wei=stop[j];
    }
    //建图的核心部分 
    for(int a=1;a<=k;a++)        //枚举停下的每一个车站 
    for(int b=tou;b<=wei;b++){    //枚举这一次路线的经过车站(包括停下的和未停下的)
        //如果b车站没有停靠，那么b车站一定比停下的所有车站等级都小，满足了建图的要求。 
        if(!vis[b]&&!gragh[b][stop[a]]){    //优化：如果以前没有边，stop[a]的入度才加一。 
            gragh[b][stop[a]]=1;            //连接一条从b指向停下的车站的边。 
            in[stop[a]]++;                    //连上边后，被指向的边的入度+1。 
        }
    }
}                                //建图完毕。
//开始拓扑排序： 
for(int i=1;i<=n;i++){            //先遍历一遍所有的点 
    if(!in[i]){                    //如果第i个点的入度为0，那么车站i一定就是等级最小的车站 
        level[i]=1;                //把等级最小的车站的等级赋值为1。 
        q.push(i);                //把入度为0的i入队，去更新其他点的level值。 
    }
}
while(!q.empty()){                //当队列不空的时候，也就是拓扑排序还没没结束的时候 
    int front=q.front();        //取出队首 
    q.pop();                    //弹出队首 
    for(int i=1;i<=n;i++){        //枚举所有的点 
        if(gragh[front][i]){    //如果队首这个点连向其他点的话 
            in[i]--;            //那么这个点的入度-1(因为队首点已经被砍掉) 
            level[i]=max(level[i],level[front]+1);//取max是为了不断更新level[i]的值。注意level[i]只能越来越大，不能越来越小。 
            if(!in[i]) q.push(i);//若入度为0，则这个点入队。 
        }
    }
    ans=max(ans,level[front]);    //随时去max，保证最后求出的ans一直是到目前为止的最大等级。 
}
cout<<ans;
return 0;
}