洛谷 P1886 滑动窗口(单调队列)
题目链接
https://www.luogu.org/problemnew/show/P1886
题目描述
现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。
例如：
The array is [1 3 -1 -3 5 3 6 7], and k = 3.
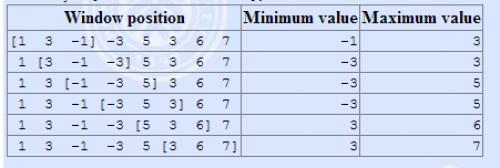
输入输出格式
输入格式：
输入一共有两行，第一行为n,k。
第二行为n个数(<INT_MAX).
输出格式：
输出共两行，第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
输入输出样例
8 3 1 3 -1 -3 5 3 6 7
-1 -3 -3 -3 3 3 3 3 5 5 6 7
说明
50%的数据，n<=10^5
100%的数据，n<=10^6
解题思路
先理解文意：对于给定一个长度为n的序列，找出所有长为k的区间的最大值（最小值）。
首先很多人会想到，枚举每一个长为k的区间，然后遍历一遍，找到最大值（最小值），这样的时间复杂度是o(nk)的，显然超时。
所以我们需要换一种思路。
单调队列：单调队列就是一个一直保持单调性(递增或递减)的长度最大为k的双端队列。
我们维护这样一个单调队列，使它队首元素即为要求的最大值（最小值）。
所以本题的核心是：怎样维护一个单调队列。
在此举例求最大值：对于任意读入的元素，我们不放设为in，首先判断队列是否为空，如果队列为空，就一定要加入队列。若不为空，就一直比较队列末尾的元素，不放设为f，如果f<in，就把f弹出去，砍掉。为什么呢？因为f能做到的，in一定也能做到，in>f，所以在一定范围内，答案有可能是in，但永远不可能是f。（这里有一个有趣的类比，如果一位OIer比你年轻还比你强，那你就没法超越他了。——Kevin大佬）。还有一个问题，就是滑动窗口长度最大是k，所以我们需要用结构体保存每一个数的编号和数值，如果in的编号和队首的编号的差>=k，就把队首砍掉，这是显然的。
这样，由于每一个元素只进入队列一次，所以时间复杂度就变成o(n)了。
话不多说，看代码。
1 #include<iostream> 2 #include<cmath> 3 #include<cstdio> 4 #include<cstring> 5 #include<string> 6 #include<cstdlib> 7 #include<queue> 8 #include<set> 9 #include<map> 10 #include<vector> 11 #include<algorithm> 12 #include<iomanip> 13 #include<ctime> //还是写了一大堆没用的头文件 14 using namespace std; 15 int n,k; 16 int maxx[1000005],minn[1000005]; //由于输出要求，需要先用数组存好答案 17 struct num{ //结构体储存编号和数值 18 int cnt,value; 19 num(int a,int b):cnt(a),value(b){} //结构体构造函数，作用是在定义结构体的时候，就会给cnt和value赋值。用法具体看29行或者39行代码 20 }; 21 deque<num> q1,q2; //定义两个双端队列，q1储存最大值，q2储存最小值 22 void makeq1(int i,int in){ //makeq1处理最大值 23 if(q1.empty()) q1.push_back(num(i,in));//队列为空时直接入队 24 else{ 25 num f=q1.front(); 26 if(i>f.cnt+k-1) q1.pop_front();//判断队列长度是否超过k 27 if(!q1.empty()){ //队尾弹不断弹出操作 28 num b=q1.back(); 29 while(b.value<in){ 30 q1.pop_back(); 31 if(q1.empty()) break; 32 b=q1.back(); 33 } 34 } 35 q1.push_back(num(i, in)); 36 } 37 } 38 void makeq2(int i,int in){ //makeq2处理最小值 39 if(q2.empty()) q2.push_back(num(i,in));//队列为空时直接入队 40 else{ 41 num f=q2.front(); 42 if(i>f.cnt+k-1) q2.pop_front(); //判断队列长度是否超过k 43 if(!q2.empty()){ //队尾弹不断弹出操作 44 num b=q2.back(); 45 while(b.value>in){ //和makeq1不同的地方 46 q2.pop_back(); 47 if(q2.empty()) break; 48 b=q2.back(); 49 } 50 } 51 q2.push_back(num(i, in)); 52 } 53 } 54 int main() 55 { 56 cin>>n>>k; 57 for(int i=1;i<=n;i++){ 58 int in; 59 cin>>in; 60 makeq1(i,in); 61 makeq2(i,in); 62 if(i>=k){ //如果长度达到k，就储存结果 63 maxx[i]=q1.front().value; 64 minn[i]=q2.front().value; 65 } 66 } 67 for(int i=k;i<=n;i++) cout<<minn[i]<<" "; //注意输出格式 68 cout<<endl; 69 for(int i=k;i<=n;i++) cout<<maxx[i]<<" "; 70 return 0; 71 }
